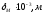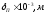Файл: бал. проектирование.docx

_{что соответствует средней ожидаемой температуре.}

Оценим меридиональное 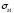и окружное 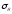напряжения в обечайке:

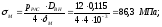
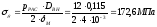
Эквивалентное напряжение составит:

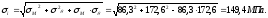
Таким образом, условие прочности обечайки выполняется, т.к.

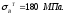
Расчет переднего днища. Пусть вылет днища 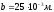При условии, что средняя ожидаемая температура днища , толщина стенки составит:

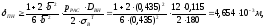
где

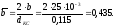
Пусть

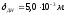
Оценим тепловое состояние днища. Для этого рассчитаем коэффициент теплоотдачи и критерии:

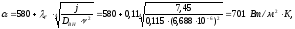
где

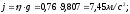
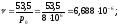
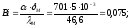
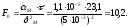
Имеем 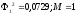, тогда

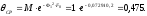
Отсюда средняя температура нетеплоизолированного днища:

,

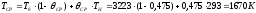что выше средней ожидаемой температуры

Поскольку полученное значение температуры выше ожидаемого, требуется теплозащитное покрытие стенки. В качестве пассивного ТЗП выбираем карбид титана.

Определим потребную толщину слоя ТЗП:

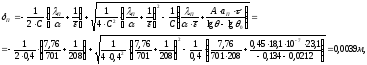
где ,

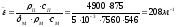Проверим фактическую температуру на границе металла и покрытия. Для этого рассчитаем критерии покрытия:

,

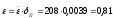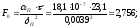
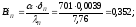
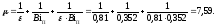
Воспользовавшись номограммой, находим θ = 0,74. Отсюда средняя температура стенки, защищенной слоем теплозащитного покрытия:

---

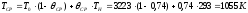
_{что соответствует средней ожидаемой температуре.}

Максимальное напряжение в днище составит:

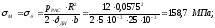
где

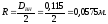
_{Таким образом, условие прочности днища выполняется, т.к.}

---

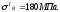
1.5.2 Расчет соплового блока рдтт

Рассчитаем коэф­фициент теплоотдачи для различных сечений соплового тракта:

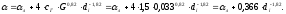
Таким образом,

• для конфузора при

;

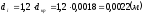
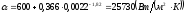• для критического сечения сопла при

;

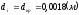
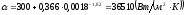• для раструба при

;

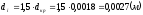
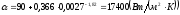• для раструба при

.

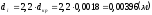
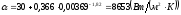Поскольку давление газов в сопловом тракте значительно ниже, чем давление в камере сгорания, в качестве допустимой температуры стенки укажем T_доп = 800°С.

Выясним, является ли процесс нагрева сопла нестационарным или темпера­тура стенки сопла достигает равновесного значения. Для этого оценим рав­новесную температуру T_р в сечениях сопла и время τ_р ее достижения:

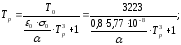
где 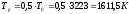- равновесное значение температуры в первом приближении;

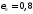– степень черноты внешней поверхности сопла;

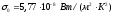- коэффициент излучения абсолютно тёмного тела.

Пусть 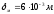- толщина стенки в первом сечении сопла

Тогда время достижения равновесной температуры в первом сечении:

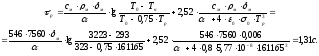
Результаты расчетов сводим в таблицу 1.

Таблица 1- Результаты расчета для различных сечений сопла

№ сечения	, мм	, Вт/(м2∙К)	, мм	Tр, С	τр, с
1	2,2	25730	6	3199	1,31
2	1,8	36510	6	3206	1,05
3	2,7	17400	6	3188	1,17
4	3,96	8653	6	3153	1,40

---

Так как время τ_р достижения равновесной температуры для всех рас­сматриваемых сечений сопла меньше времени работы двигателя (τ =23,1 с), то имеет место стационарная теплопроводность.

В качестве ТЗП принимаем фторопласт.

Потребная толщина слоя ТЗП для первого сечения составит:

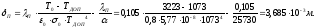
При этом температура поверхности покрытия составит:

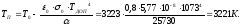
Результаты счёта в остальных сечениях указаны в таблице 2.

Таблица 2 - Результаты расчета толщины ТЗП и средней температуры стенки

№ сечения
1	6	3,685	3221
2	6	3,687	3222
3	6	3,683	3219
4	6	3,677	3216

1.6 Расчет размеров стабилизирующего оперения

1.6.1 Расчет стабилизаторов

Требуется оценить размеры стабилизирующего оперения и аэродинамических рулей при следующих исходных данных:  = 4 - угол атаки; V= 225 м/с - скорость полета; ξ = 15% - запас устойчивости;  =15° - угол поворота; d = 125 мм - калибр ракеты; 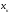= 695 мм - длина кор­пуса.

Определим эксцентриситет ракеты:

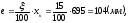
Найдем координату центра тяжести ракеты по формуле:

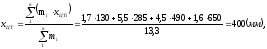
тогда координата центра давления ракеты:

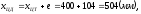
Так как режим полета дозвуковой, то коэффициент подъемной силы корпуса ракеты составит:

---

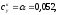
При этом координата центра давления корпуса:

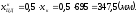
Известно, что 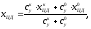отсюда

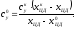
Пусть ,

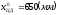тогда

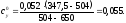
Рассчитаем коэффициент подъемной силы:

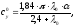
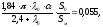
Отсюда

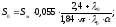
Пусть 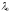= 1,4,

,

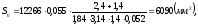
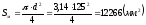где S_м - мидель ракеты; S₀ - площадь стабилизирующего оперения.

Площадь пера стабилизатора для крестообразного оперения:

.

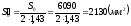Пусть стабилизатор имеет прямоугольную форму в плане, тогда

,

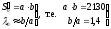где а - хорда стабилизатора; b - длина стабилизатора.

Решая полученную систему уравнений, найдем потребные размеры пера крестообразного стабилизирующего оперения:

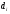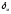а = 39 (мм); b = 55 (мм).

---