Файл: Тема 8.doc

Расчет ошибок при определении границ генеральной доли, т.е. доли единиц, обладающих тем или иным вариантом изучаемого признака, основан на теореме Бернулли. Согласно этой теореме, вероятность сколь угодно малого расхождения между выборочной долей и генеральной долей при достаточно большом объеме выборки будет стремиться к единице. С учетом того, что вероятность расхождения между выборочной и генеральной долями подчиняется нормальному закону распределения, при определении предельной ошибки выборочной доли также используется функция при заданном значении.

В целом процесс подготовки и проведения выборочного наблюдения включает ряд последовательных этапов, представленных на рис.8.2. В зависимости от состава и структуры генеральной совокупности выбирается вид выборки, или способ отбора. К наиболее распространенным на практике видам относятся:

• собственно-случайная (простая случайная) выборка;

• механическая (систематическая) выборка;

• типическая (стратифицированная, расслоенная) выборка;

• серийная (гнездовая) выборка.

Отбор единиц из генеральной совокупности может быть комбинированным, многоступенчатым и многофазным.

Комбинированный отбор предполагает объединение нескольких видов выборки. Так, например, можно комбинировать типическую и серийную, серийную и собственно-случайную выборки. Ошибка такой выборки определяется ступенчатостью отбора.

Многоступенчатым называется отбор, при котором из генеральной совокупности сначала извлекаются укрупненные группы, потом - более мелкие и так до тех пор, пока не будут отобраны те единицы, которые подвергаются обследованию.

В отличие от многоступенчатой многофазная выборка предполагает сохранение одной и той же единицы отбора на всех этапах его проведения; при этом отобранные на каждой стадии единицы подвергаются обследованию (программа обследования на каждой последующей стадии отбора расширяется).

Любой вид выборки или их комбинация предполагает использование тех или иных методов непосредственного отбора единиц (групп единиц), основанных на специальных алгоритмах, реализующих принцип случайности. Рассмотрению этих методов и посвящен раздел 8.2.

---

---

8.2 Методы (алгоритмы) отбора единиц в выборочную совокупность

Процесс формирования выборочной совокупности основан на принципе случайности, реализация которого обеспечивается применением соответствующих методов, или алгоритмов, отбора единиц. В простейшем варианте отбор единиц в выборочную совокупность может быть проведен методом жеребьевки. Для этого необходимо располагать достаточным количеством жребиев (фишек, карточек), соответствующих объему генеральной совокупности. Каждый жребий должен содержать информацию об отдельной единице совокупности - номер, название, фамилию лица, адрес или какой-либо другой отличительный признак. Требуемое в соответствии с установленным процентом отбора число жребиев извлекается из общей совокупности в случайном порядке.

Жеребьевка является в большей степени теоретическим методом формирования выборки, так как ее техническая реализация при большом объеме генеральной совокупности затруднительна. Используемые же на практике методы отбора единиц в выборочную совокупность базируются на специальных алгоритмах, реализующих принцип случайности. Рассмотрим некоторые из них.

Метод случайной сортировки включает три шага:

1. Каждой единице генеральной совокупности присваивается случайное число , полученное с помощью процессора случайных чисел в интервале от 0 до 1 (полученные случайные числа должны в той или иной степени соответствовать закону равномерного распределения). Отметим, что генерация случайных чисел может быть произведена вMicrosoftExcel(Вставка функции - Математические - Случайное число).

2. Единицы генеральной совокупности ранжируются в соответствии с полученным значением .

3. Отбираются 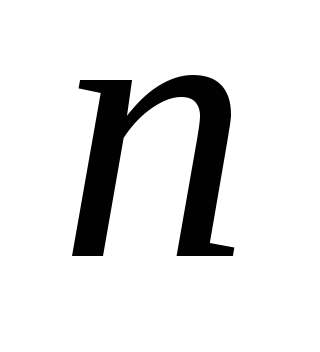первых единиц.

Достоинства данного метода заключаются в простом алгоритме отбора единиц, а также в возможности формирования нескольких выборок без перекрытия. К недостатку данного метода относят наличие процедуры сортировки единиц генеральной совокупности, которая при достаточно большом ее объеме нежелательна.

Метод прямой реализации предполагает следующую последовательность действий:

---

1. Все единицы генеральной совокупности, расположенные в случайном порядке или ранжированные по какому-либо признаку, нумеруются от 1 до .

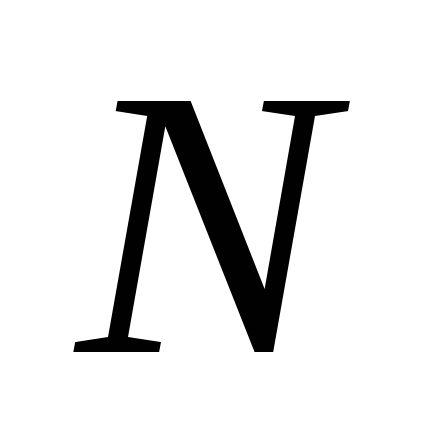2. С помощью процессора случайных чисел получают 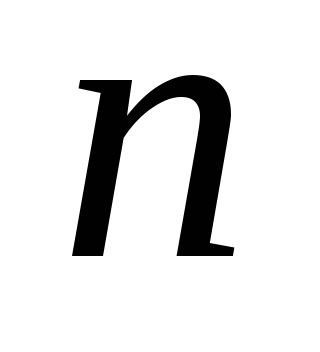значений в интервале от 1 до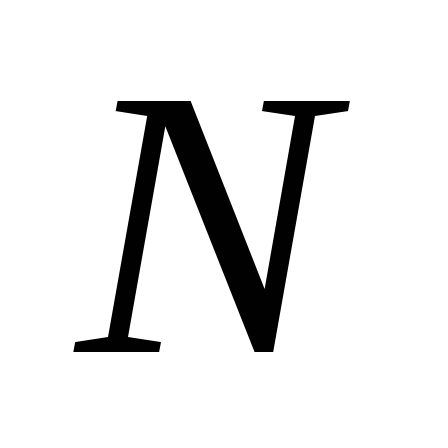. Если первоначально случайные числа получены в интервале от 0 до 1, их необходимо умножить на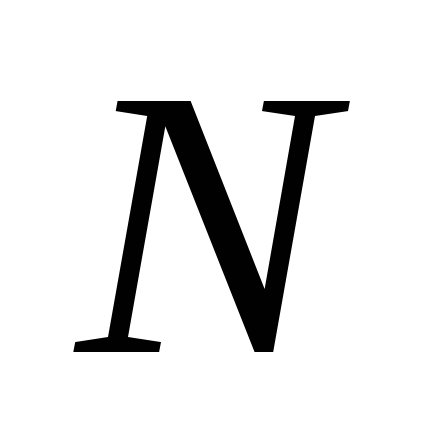 и округлить по правилам до целого значения.

3. Из сформированного списка единиц генеральной совокупности отбираются единицы, соответствующие по номеру полученным случайным числам.

Отметим, что если полученные в п. 2 случайные числа ранжировать, то реализация данного алгоритма потребует только одного считывания файла единиц генеральной совокупности.

Упрощенным вариантом метода прямой реализации является отбор единиц в выборочную совокупность на основе таблицы случайных чисел (см. приложение 15). Для проведения отбора могут быть использованы цифры любого столбца данной таблицы, при этом необходимо учитывать объем генеральной совокупности.

Рассмотрим процедуру отбора на основе фрагмента таблицы случайных чисел. Предположим, объем генеральной совокупности составляет 70 000 ед. и требуется сформировать выборку объемом 500 ед.; тогда цифры таблицы следует перегруппировать для получения пятизначных чисел следующим образом:

5489	5	583	31	56	083	5	1988
3522	0	935	78	77	566	5	7020
7555	7	579	25	50	248	7	9477
5759	3	554	50	80	907	4	7001
6303	6	895	33	71	319	6	7231

---

Для формирования выборки мы должны взять 500 чисел в интервале от 00001 до 70000. Таким образом, нам следует из списка единиц генеральной совокупности отобрать единицы под номером 54895, 35220, 57593 и т.д. При этом номера свыше 70000 (75557, 93578 и подобные) будут проигнорированы.

При проведении бесповторного отбора повторяющиеся номера следует учитывать только один раз. При повторном отборе, если тот или иной номер случайно встретится еще один или более раз, соответствующая этому номеру единица в каждом случае повторно включается в выборочную совокупность.

Метод отбора-отказа включает следующие итерации:

• последовательно образуют случайные числа 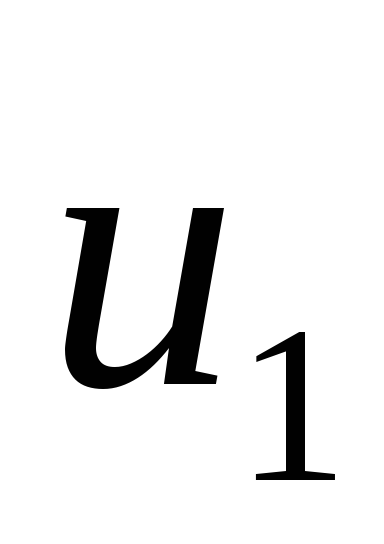, 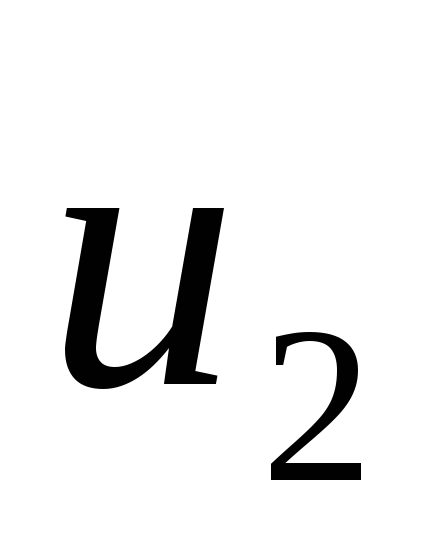... в соответствии с законом равномерного распределения в интервале от 0 до 1;

• для первой единицы генеральной совокупности проверяется выполнение следующего неравенства:

.

(8.1)

Если данное неравенство выполняется, то первая единица включается в выборку, в противном случае - нет;

• для оставшихся единиц последовательно проверяется выполнение неравенства

(8.2)

где - число отобранных в выборку единиц среди первых просмотренных единиц. Если для-й единицы это неравенство выполняется, то данная единица включается в выборку, в противном случае - нет;

• процедура заканчивается, когд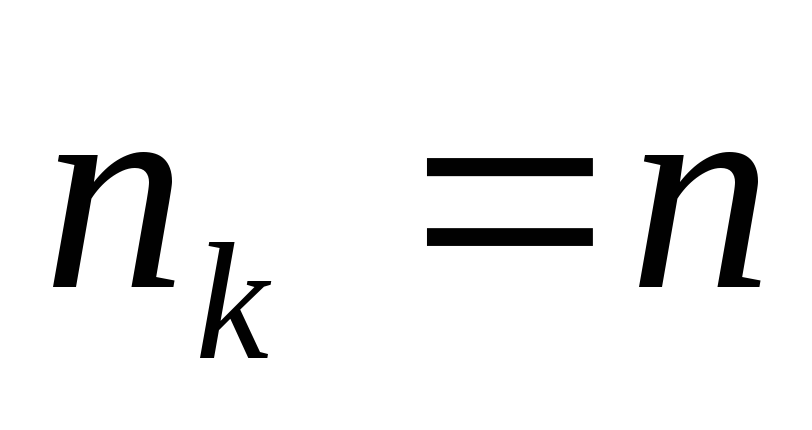а , т. е. когда выборка необходимого объема полностью сформирована. Этот момент вполне может наступить и до завершения полного просмотра всех единиц генеральной совокупности. Следует отметить, что данный метод основан на алгоритме последовательного извлечения единиц, не требующем ни предварительной сортировки единиц генеральной совокупности или образованных случайных чисел, ни многократного считывания исходного файла.

---