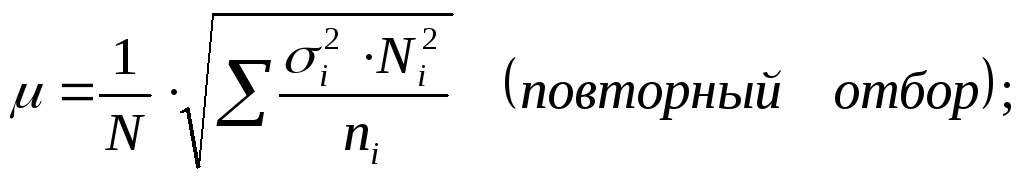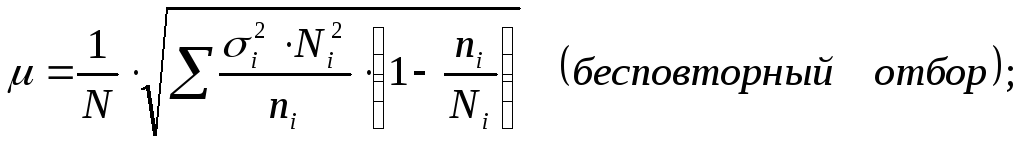ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.08.2024
Просмотров: 89
Скачиваний: 0
СОДЕРЖАНИЕ
Значение и теоретические основы выборочного наблюдения
8.2 Методы (алгоритмы) отбора единиц в выборочную совокупность
8.3 Собственно-случайная (простая случайная) выборка
8.4 Механическая (систематическая) выборка
8.5 Типическая (стратифицированная) выборка
8.7 Практика применения выборочного наблюдения в социально-экономических исследованиях
Опасность систематической ошибки пли механической выборке также может появиться вследствие случайного совпадения выбранного интервала и циклических закономерностей в расположении единиц генеральной совокупности. Так, при переписи населения 1989 г. в ходе 25%-го выборочного обследования семей была опасность попадания в выборку квартир только одного типа (например, только однокомнатных или только трехкомнатных), так как на лестничных площадках многих типовых домов располагаются именно по 4 квартиры. Чтобы избежать систематической ошибки, в каждом новом подъезде счетчик менял начало отбора.
Для определения средней ошибки механической выборки, а также необходимой ее численности используются соответствующие формулы, применяемые при собственно-случайном бесповторном отборе, формулы (8.6) и (8.9). При этом, определив необходимую численность выборки и сопоставив ее с объемом генеральной совокупности, как правило, приходится производить соответствующее округление для получения целочисленного интервала отбора.
8.5 Типическая (стратифицированная) выборка
Типический отбор целесообразно использовать в тех случаях, когда все единицы генеральной совокупности объединены в несколько крупных типических групп. Такие группы также называют стратами, или слоями, в связи с чем типический отбор также называютстратифицированным, илирасслоенным. При обследовании населения в качестве типических групп могут быть выбраны области, районы, социальные, возрастные или образовательные группы, при обследовании предприятий - отрасли или подотрасли, формы собственности и т.п.
Рассматривать генеральную совокупность в разрезе нескольких крупных групп единиц имеет смысл только в том случае, если средние значения изучаемых признаков по группам существенно различаются. Например, с большой уверенностью можно предположить, что доходы населения крупного города будут в среднем выше доходов населения, проживающего в сельской местности; численность работников промышленного предприятия в среднем будет выше численности работников торгового или сельскохозяйственного предприятия; средний возраст студентов будет значительно ниже среднего возраста занятого населения, и тем более пенсионеров. В то же время нет никакого смысла при выделении типических групп ориентироваться на признак, не связанный или очень слабо связанный с изучаемым. Например, при изучении доходов населения вряд ли улучшению результатов выборочного обследования будет способствовать деление населения на группы на основе первой буквы фамилии, так как маловероятно, что доходы людей, чья фамилия начинается с букв в интервале от А до К, будут существенно выше или ниже доходов лиц, носящих фамилию, начинающуюся с букв в интервале Л-Я.
Отбор единиц в выборочную совокупность из каждой типической группы осуществляется собственно-случайным или механическим способом. Поскольку в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, типизация генеральной совокупности позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки. В то же время в выделенных типических группах обследуются далеко не все единицы, а только включенные в выборку. Следовательно, на величину полученной ошибки будет влиять различие между единицами внутри этих групп, т.е. внутригрупповая вариация. Поэтому ошибка типической выборки будет определяться величиной не общей дисперсии, а только ее части - средней из внутригрупповых дисперсий.
Отбор единиц в типическую выборку может быть организован либо пропорционально объему типических групп, либо пропорционально внутригрупповой вариации (дифференциации) признака.
При типической выборке, пропорциональной объему типических групп, число единиц, подлежащих отбору из каждой группы, определяется следующим образом:
|
|
(8.10) |
где
![]() - объем
- объем![]() -и
группы;
-и
группы;
![]() - объем выборки из
- объем выборки из![]() -й
группы.
-й
группы.
Средняя ошибка типической выборки определяется по формулам:
|
|
(8.11) |
|
|
(8.12) |
где
![]() - средняя из внутригрупповых дисперсий.
- средняя из внутригрупповых дисперсий.
При определении необходимого объема типической выборки в рассмотренных выше формулах (8.11) и (8.12) общую дисперсию наблюдаемого признака необходимо заменить на среднюю из внутри-групповых дисперсий. Тогда данные формулы примут следующий вид:
|
|
(8.13) |
|
|
(8.14) |
Мы рассмотрели типический отбор, пропорциональный объему типических групп. Второй вариант формирования типической выборки заключается в отборе единиц, пропорциональном вариации признака в типических группах. Логика такого отбора заключается в следующем: если внутри какой-либо типической группы наблюдаемый признак варьирует слабо, то для определения границ генеральных характеристик из данной группы достаточно обследовать относительно небольшое число единиц; при сильной же вариации признака объем выборки должен быть соответственно увеличен.
При выборке, пропорциональной вариации признака, число наблюдений по каждой группе рассчитывается по формуле:
|
|
(8.15) |
где
![]() - среднее квадратическое отклонение
признака в
- среднее квадратическое отклонение
признака в![]() -й
группе.
-й
группе.
Средняя ошибка такого отбора определяется следующим образом:
|
|
(8.16) |
|
|
(8.17) |
Отбор, пропорциональный вариации признака, дает лучшие результаты, однако на практике его применение затруднено из-за трудности получения сведений о вариации до проведения выборочного наблюдения.
8.6 Серийная выборка
Сущность серийной выборки заключается в собственно-случайном либо механическом отборе групп единиц (серий), внутри которых производится сплошное обследование. Единицей отбора при этой выборке являетсягруппа илисерия, а не отдельная единица генеральной совокупности, как это имело место в рассматриваемых ранее выборках.
Данный способ отбора удобен в тех случаях, когда единицы генеральной совокупности изначально объединены в небольшие более или менее равновеликие группы или серии. В качестве таких серий могут выступать упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и другие подобные объединения. Например, в Великобритании серийный отбор используется в обследованиях населения, когда серией являются домохозяйства, объединенные общим почтовым индексом. В случайном порядке производится выборка индексов, и под обследование попадают все домохозяйства, имеющие индекс попавших в выборочную совокупность почтовых отделений.
В отдельных случаях серийная выборка имеет не столько методологические, сколько организационные преимущества перед другими способами формирования выборочной совокупности. Например, Управление маркетинга и регионального развития Московского государственного университета экономики, статистики и информатики периодически проводит обследования школьников Москвы. С организационной точки зрения достаточно сложно опрашивать отдельных учеников из разных классов. Значительно проще из общего списка всех классов всех школ округа сформировать выборку классов, а внутри отобранных классов провести 100%-е обследование учащихся.
В связи с тем что при серийном отборе внутри отобранных групп обследуются все без исключения единицы, внутригрупповая вариация признака не отразится на ошибках выборочного наблюдения. В то же время обследуются не все группы, а только попавшие в выборку. Следовательно, на ошибках получаемых характеристик отразятся различия между группами, которые определяются межгрупповой дисперсией. Поэтому средняя ошибка серийной выборки рассчитывается по формулам
|
|
(8.18) |
|
|
(8.19) |