Файл: Применение алгоритмов поиска в массивах.pdf

ВВЕДЕНИЕ

Актуальность данной работы состоит в том, что на сегодняшний день больше половины жителей планеты земля пользуются компьютером. Большая часть из них начинают свою работу с поиска необходимой информации в различных источниках, будь то интернет, базы данных или поиск файлов на локальном диске, и если время поиска увеличить хотя бы на секунду, то общее время, затраченное всеми пользователями на поиск необходимой информации перевалит за 200 лет. Поэтому так важно разрабатывать, поддерживать и внедрять такие алгоритмы поиска, которые позволят сократить время поиска до минимума. По словам вице-президента по инфраструктуре Google Урса Хельцле: «У нас есть одно простое правило, чтобы поддержания скорости: не запускайте функции, которые замедляют процесс поиска. Можно изобрести отличный новый алгоритм, но если он замедляет поиск, вам придется либо забыть о нем, либо исправить его, либо придумать другое изменение, которое более чем компенсирует замедление. У нас есть то, что мы называем "фиксированным бюджетом задержки", который похож на семейный бюджет. Если вы хотите поехать в более приятный отпуск, но ваш бюджет не растягивается, вам нужно сократить его где-то еще».

Именно по этой причине во многих уважающих себя компаниях по разработке программного обеспечения, особое внимание отводится скорости работы программного обеспечения в общем и разработке эффективных поисковых алгоритмов в частности, постоянно отслеживается производительность, чтобы команда разработчиков могла видеть уровни задержки в сервисах. Вот почему несколько лет назад, когда все начало замедляться, основной упор был сделан на то, чтобы делать продукты быстрее. Скорость - это важная часть инженерной культуры.

Основой быстрого поиска является разработка эффективных поисковых алгоритмов, позволяющих не только быстро найти информацию, но и сделать так, чтобы данная информация соответствовала запросу, поэтому целью данной курсовой работы является изучение и анализ поисковых алгоритмов.

Для достижения поставленной цели в курсовой работе необходимо решить следующие задачи:

1. Изучить виды поисковых алгоритмов в матрице
2. Понять какие должны быть входные данные и как обработать полученные результат
3. Реализовать изученные алгоритмы в программном коде.
4. Сделать анализ алгоритма.
5. Найти наиболее эффективный алгоритм поиска.

При написании курсовой работы использовалась специализированная литература следующих авторов: Джордж Хайнеман [1], Готтшлинг П. [2], Страуструп Б. [4]

1. ОСНОВНЫЕ ВИДЫ АЛГОРИТМОВ ПОИСКА В МАССИВАХ

1.1 Последовательный поиск

Последовательный поиск (Sequential Search), называемый также линейным поиском, является самым простым из всех алгоритмов поиска. Это метод поиска одного значения в коллекции “в лоб”. Он находит значение, начиная с первого элемента коллекции и исследуя каждый последующий элемент до тех пор, пока не просмотрит всю коллекцию или пока соответствующий элемент не будет найден. Для работы этого алгоритма должен иметься способ получения каждого элемента из коллекции, в которой выполняется поиск; порядок извлечения значения не имеет. Часто элементы коллекции могут быть доступны только через итератору который предназначен только для чтения и получает каждый элемент из коллекции.

Входные данные представляют собой непустую коллекцию и целевое значение, которое мы ищем. Поиск возвращает true, если коллекция содержит целевое значение и false в противном случае.

Зачастую требуется найти элемент в коллекции, которая может быть не упорядочена. Без дополнительных знаний об информации, хранящейся в коллекции, последовательный поиск выполняет работу методом “грубой силы”. Это единственный алгоритм поиска, который можно использовать, если коллекция доступна только через итератор.

Если коллекция неупорядоченная и хранится в виде связанного списка, то вставка элемента является операцией с константным временем выполнения (он просто добавляется в конец списка). Частые вставки в коллекцию на основе массива требуют управления динамической памятью, которое либо предоставляется базовым языком программирования, либо требует определенного внимания со стороны программиста.

Последовательный поиск накладывает наименьшее количество ограничений на типы искомых элементов. Единственным требованием является наличие функции проверки совпадения элементов, необходимой для выяснения, соответствует ли искомый элемент элементу коллекции; часто эта функция возлагается на сами элементы.

1.2 Бинарный поиск

Бинарный (двоичный) поиск обеспечивает лучшую производительность, чем последовательный поиск, поскольку работает с коллекцией, элементы которой уже отсортированы. Бинарный поиск многократно делит отсортированную коллекцию пополам, пока не будет найден искомый элемент или пока не будет установлено, что элемент в коллекции отсутствует.

Входными данными для бинарного поиска является индексируемая коллекция, элементы которой полностью упорядочены, а это означает, что для двух индексов, i и j, A[i] < A[j] только тогда, когда i < j. Сроится структура данных, которая хранит элементы (или указатели на элементы) и сохраняет порядок ключей. Выходные данные бинарного поиска, как и последовательного поиска — true или false.

Для поиска по упорядоченной коллекции в худшем случае необходимо логарифмическое количество проб.

Бинарный поиск поддерживают различные типы структур данных. Если коллекция никогда не изменяется, элементы следует поместить в массив (это позволяет легко перемещаться по коллекции). Однако, если необходимо добавить или удалить элементы из коллекции, этот подход становится неудачным и требует дополнительных расходов. Есть несколько структур данных, которые мы можем использовать в этом случае одной из наиболее известных является бинарное дерево поиска.

1.3 Поиск на основе Хеша

Если требуются более мощные методы поиска в больших коллекциях, в которых данные не обязательно упорядочены, то одним из наиболее распространенных подходов к решению этой задачи является использование хеш-функции для преобразования одной или нескольких характеристик искомого элемента в индекс в хеш-таблице. Поиск на основе хеша (Hash-Based Search) имеет в среднем случае производительность, которая лучше производительности любого другого алгоритма поиска.

В поиске на основе хеша элементы коллекции сначала загружаются в хеш-таблицу, структурированными в виде массива. Этот шаг предварительной обработки имеет свою отдельную производительность, но улучшает производительность будущих поисков с использованием концепции хеш-функции.

Хеш-функция представляет собой детерминированную функцию, которая отображает каждый элемент коллекции целочисленным значением. При загрузке элементов в хеш-таблицу элемент коллекции вставляется в ячейку хеш-таблицы. После того как все элементы будут вставлены, поиск элемента коллекции становится поиском этого элемента в хеш-таблице.

Может случиться так, что несколько элементов в коллекции имеют одинаковые значения хеша. Такая ситуация называется коллизией, и хеш-таблице необходима стратегия для урегулирования подобных ситуаций. Наиболее распространенным решением является хранение в каждой ячейке связанного списка (несмотря на то, что многие из этих связанных списков будут содержать только один элемент); при этом в хеш-таблице могут храниться все элементы, вызывающие коллизии. Поиск в связанных списках должен выполняться линейно, но он будет быстрым, потому что каждый из них может хранить максимум несколько элементов. Общая схема поиска на основе хеша показана на рис. 1. Ее компонентами являются:

• множество U, которое определяет множество возможных хеш-значений. Каждый элемент е ∈ С отображается на хеш-значение h ∈ U;

• хеш-таблица Н, содержащая b ячеек, в которых хранятся n элементов из исходной коллекции С;

• хеш-функция hash, которая вычисляет целочисленное значение h для каждого элемента е, где 0 ≤ h < b.

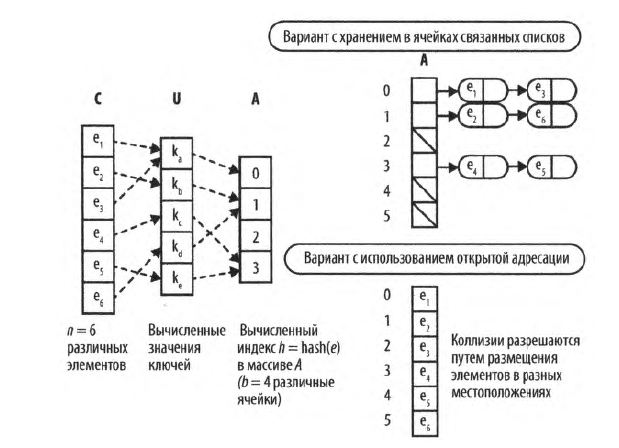
рис. 1. Схема хеширования

Эта информация хранится в памяти с использованием массивов и связанных списков.

У поиска на основе хеша имеются две основные проблемы: разработка хеш-функции и обработка коллизий. Плохо выбранная хеш-функция может привести к плохому распределению ключей в первичной памяти с двумя последствиями: а) многие ячейки в хеш-таблице могут остаться неиспользованными и зря тратить память, и б) будет иметься много коллизий, когда много ключей попадают в одну и ту же ячейку, что существенно ухудшает производительность поиска.

В отличие от бинарного поиска при поиске на основе хеша исходная коллекция не обязана быть упорядоченной. Действительно, даже если элементы коллекции были некоторым образом упорядочены, метод хеширования, вставляющий элементы в хеш-таблицу не пытается в ней воспроизвести этот порядок.

Входными данными для поиска на основе хеша являются вычисленная хеш-таблица и искомый элемент. Алгоритм возвращает true, если искомый элемент имеется в связанном списке, хранящемся в хеш-таблице. Если искомый элемент в связанном списке, хранящемся в хеш-таблице отсутствует, возвращается значение false, указывающее, что искомого значения нет в хеш-таблице (и, таким образом, его нет в коллекции).

При поиске на основе хеша количество сравнений строк связано с длиной связанных списков, а не с размером коллекции. Сначала необходимо определить хеш-функцию. Цель заключается в том, чтобы получить как можно больше различных значений, но не все эти значения обязаны быть уникальными. Хеширование изучалось на протяжении десятилетий, и в многочисленных работах описано множество эффективных хеш-функций, но они могут использоваться для гораздо большего, чем простой поиск. Например, специальные хеш-функции имеют важное значение для криптографии. Для поиска хеш-функция должна обладать хорошим равномерным распределением и быть быстро вычисляемой за малое количество тактов процессора.

1.4 Фильтр Блума

Фильтр Блума предоставляет альтернативную структуру битового массива, которая обеспечивает константную производительность при добавлении элементов из коллекции в битовый массив или проверку того, что элемент не был добавлен в этот массив. Как ни удивительно, то поведение не зависит от количества элементов, уже добавленных в массив. Однако имеется и ловушка: при проверке, находится ли некоторый элемент в массиве, фильтр Блума может возвратить ложный положительный результату даже если на самом деле элемент в коллекции отсутствует. Фильтр Блума позволяет точно определить, что элемент не был добавлен в массив, поэтому никогда не возвращает ложный отрицательный результат.

На рис. 2 в битовый массив вставлены два значения u и v. Таблица в верхней части рисунка показывает позиции битов, вычисленные хеш-функциями. Как можно видеть, фильтр Блума в состоянии быстро определить, что третье значение w не было вставлено в массив, поскольку одно из его вычисляемых хеш-функциями значений битов равно нулю (в данном случае это бит 6). Однако для значения х фильтр возвращает ложный положительный результат, поскольку, несмотря на то что это значение не было вставлено в массив, все вычисляемые значения битов равны единице.

рис. 2. Фильтр Блума. Пример работы.

Фильтр Блума обрабатывает значения во многом так же, как и поиск на основе хеша. Алгоритм начинает работу с массива из битов, каждый из которых изначально равен нулю. Имеется несколько хеш-функций, вычисляющих при вставке значений (потенциально различные) позиции битов в этом массиве.

Фильтр Блума возвращает значение false, если может доказать, что целевой элемент еще не был вставлен в битовый массив и, соответственно, отсутствует в коллекции. Алгоритм может вернуть значение true, которое может быть ложным положительным результатом, если искомый элемент не был вставлен в массив.

Фильтр Блума демонстрирует эффективное использование памяти, но он полезен только тогда, когда допустимы ложные положительные результаты. Фильтр Блума используется для снижения количества дорогостоящих поисков путем отбрасывания тех, которые гарантированно обречены на провал, например, для подтверждения проведения дорогостоящего поиска на диске.

1.5 Бинарное дерево поиска

Бинарный поиск в массиве в памяти, как мы уже видели, достаточно эффективен. Однако, использование упорядоченных массивов становится гораздо менее эффективным при частых изменениях базовой коллекции. При работе с динамической коллекцией для поддержания приемлемой производительности поиска необходимо использовать иную структуру данных. Поиск на основе хеша может работать с динамическими коллекциями, но с целью эффективного использования ресурсов можно выбрать размер хеш-таблицы, который окажется слишком мал; зачастую нет априорного знания о количестве элементов, которые будут храниться в таблице, так что выбрать правильный размер хеш-таблицы оказывается очень трудной задачей. Кроме того, хеш-таблицы не позволяют обходить все элементы в порядке сортировки.