Добавлен: 29.03.2023
Просмотров: 330
Скачиваний: 7
СОДЕРЖАНИЕ
1. ОСНОВНЫЕ ВИДЫ АЛГОРИТМОВ ПОИСКА В МАССИВАХ
2. РЕАЛИЗАЦИЯ И АНАЛИЗ АЛГОРИТМОВ
2.1 Последовательный поиск. Реализация. Анализ
2.2 Бинарный поиск. Реализация. Анализ
2.3 Поиск на основе Хеша. Реализация. Анализ
2.4 Фильтр Блума. Реализация. Анализ
2.5 Бинарное дерево поиска. Реализация. Анализ
Пока хеш-функция достаточно равномерно распределяет элементы коллекции, поиск, основанный на хеше, имеет отличную производительность. Среднее время, необходимое для поиска элемента, является константой, или 0(1). Поиск состоит из одного просмотра Н с последующим линейным поиском в коротком списке коллизий.
Компонентами поиска элемента в хеш-таблице являются:
• вычисление хеш-значения;
• доступ к элементу таблицы, индексированному хеш-значением;
• поиск требуемого элемента при наличии коллизий.
Все алгоритмы поиска на основе хеша используют первые два компонента; различное поведение может наблюдаться только в разных вариантах обработки коллизий. Стоимость вычисления хеш-значения должна быть ограничена фиксированной, константной верхней границей.
Время поиска элементов в хеш-таблице не зависит от количества элементов в хеш- таблице (поиск имеет фиксированную стоимость), так что алгоритм поиска на основе хеша имеет амортизированную производительность 0(1). [1]
2.4 Фильтр Блума. Реализация. Анализ
Реализовать структуру данных фильтра Блума можно разделив ее интрефейс на 3 основные функции:
- Конструктор
- Функция, чтобы добавить элемент к фильтру Блума
- Функция для запроса является ли искомый элемент элементом фильтра Блума.
Реализация фильтра Блума в приложении Г [4]. В данной реализации используется MurmurHash3 (https://github.com/aappleby/smhasher/tree/master
/src), для вычисления 128 битного хеша элемента.
Общее количество памяти, необходимое для работы фильтра Блума, фиксировано, и оно не увеличивается независимо от количества хранящихся значений. Кроме того, алгоритм требует только фиксированного количества испытаний k, поэтому каждая вставка и поиск могут быть выполнены за время 0(k), которое рассматривается как константное.
Основная сложность фильтра заключается в разработке эффективных хеш-функций, которые обеспечивают действительно равномерное распределение вычисляемых битов для вставляемых значений. Хотя размер битового массива является константой, для снижения количества ложных положительных срабатываний он может быть достаточно большим. И наконец, нет никакой возможности удаления элемента из фильтра, поскольку потенциально это может фатально нарушить обработку других значений.
Единственная причина для использования фильтра Блума заключается в том, что он имеет предсказуемую вероятность ложного положительного срабатывания в предположении, что к хеш-функций дают равномерно распределенные случайные величины.
2.5 Бинарное дерево поиска. Реализация. Анализ
В приложении Д реализовано простое несбалансированное бинарное дерево поиска.
В бинарном дереве поиска может быть несколько элементов с одинаковыми значениями, но, если необходимо ограничить дерево семантикой множества можно изменить код так, чтобы он предотвращал вставку повторяющихся ключей.
Эффективность реализации зависит от сбалансированности BST. Для сбалансированного дерева размер множества, в котором выполняется поиск, уменьшается в два раза при каждой итерации, что приводит к производительности O(log n). Однако для вырожденных бинарных деревьев, производительность равна О(n). Для сохранения оптимальной производительности необходимо балансировать BST после каждого добавления (и удаления).
AVL-деревья (названные так в честь их изобретателей, Адельсона-Вельского и Ландиса), изобретенные в 1962 году, были первыми самобалансирующимися BST. Высота листа равна 0, потому что он не имеет дочерних элементов. Высота узла, не являющегося листом, на 1 больше максимального значения высоты двух его дочерних узлов. Для обеспечения согласованности высота несуществующего дочернего узла считается равной -1. AVL-дерево гарантирует AVL-свойство для каждого узла, заключающееся в том, что разница высот для любого узла равна -1, 0 или 1. Разница высот определяется как height(left) - height(right), т.е. высота левого поддерева минус высота правого поддерева. AVL-дерево должно обеспечивать выполнение этого свойства всякий раз при вставке значения в дерево или удалении из него. Каждый узел в дереве AVL хранит свое значение высоты Height, что увеличивает общие требования к памяти.
На рис. 5 показано, что происходит при вставке значений 50, 30 и 10 в дерево в указанном порядке.
Рис. 5. Сбалансированное и несбалансированное бинарное дерево поиска.
Получаемое дерево не удовлетворяет AVL-свойству, так как высота корня левого поддерева равна 1, а высота его несуществующего поддерева справа равна -1, так что разница высот равна 2. Если “захватить” узел 30 исходного дерева и повернули дерево вправо (или по часовой стрелке) вокруг узла 30 так, чтобы сделать узел 30 корнем, создав тем самым сбалансированное дерево. При этом изменяется только высота узла 50 (снижается от 2 до 0) и AVL-свойство дерева восстанавливается.
Операция поворота вправо изменяет структуру поддерева в несбалансированном BST; очевидно, что имеется и аналогичная операция поворота влево. Если это дерево имеет и другие узлы, каждый из которых был сбалансирован и удовлетворял AVL-свойству, такое дерево можно модифицировать. На рис. 6 каждый из заштрихованных треугольников представляет собой потенциальное поддерево исходного дерева. Каждое из них помечено в соответствии с его позицией, так что поддерево 30R представляет собой правое поддерево узла 30. Корень является единственным узлом, который не поддерживает AVL-свойство. Различные показанные на рисунке высоты в дереве вычислены в предположении, что узел 10 имеет некоторую высоту k.
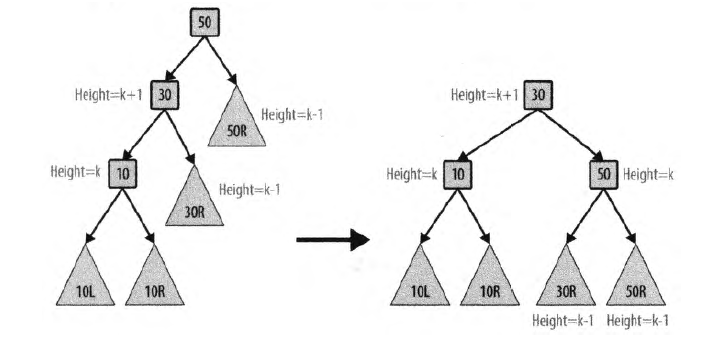
Рис.6 Сбалансированное AVL-дерево с поддеревьями
Модифицированное бинарное дерево поиска по-прежнему гарантирует свойство бинарного поиска. Все значения ключей в поддереве 30R больше или равны 30. Позиции других поддеревьев одно относительно другого не изменились, так что свойство бинарного поиска остается выполненным. Наконец значение 30 меньше значения 50, так что новый корневой узел вполне корректен.
Производительность поиска в сбалансированном AVL-дереве в среднем случае совпадает с производительностью бинарного поиска (т.е. равна 0(log n)). Следует отметить, что в процессе поиска никакие повороты не выполняются. Самобалансирующиеся бинарные деревья требуют более сложного кода вставки и удаления, чем простые бинарные деревья поиска. Пересмотрев методы поворотов, очевидно, что каждый из них состоит из фиксированного количества операций, так что их можно рассматривать как выполняющиеся за константное время. Высота сбалансированного AVL-дерева благодаря поворотам всегда будет иметь порядок 0(log n). Таким образом, при добавлении или удалении элемента никогда не будет выполняться больше чем 0(log n) поворотов. Таким образом, можно быть уверенным, что вставки и удаления могут выполняться за время 0(log n). Компромисс, состоящий в том, что AVL-деревья хранят значения высоты в каждом узле (что увеличивает расход памяти), обычно стоит получаемой при этом гарантированной производительности.
ЗАКЛЮЧЕНИЕ
В курсовой работе рассмотрены и изучены виды алгоритмов поиска в массивах, рассмотрены входные данные и получаемые результаты, по каждому алгоритму сделан анализ зависимости начальных данных к скорости работы.
Наиболее эффективный алгоритм найден не был, так как использование конкретных алгоритмов поиска сильно зависит от области и условий его применения. Так, например, последовательный поиск используется в небольших коллекциях данных и предлагает простейшую реализацию и во многих языках программирования реализуется в виде базовой конструкции, поэтому данный алгоритм используется, если коллекция доступна только последовательно, как при использовании итераторов. Бинарный поиск используется в условиях ограниченной памяти, когда коллекция представляет собой неизменный массив и есть необходимость сэкономить память. Поиск на основе хеша очевидно стоит использовать, когда данные часто динамически меняются. Так же в этом случае стоит применять и бинарное дерево поиска, так как данные алгоритмы обладают пониженной стоимостью, связанной с поддержанием их структур данных. Так же бинарное дерево стоит использовать в тех случаях, когда помимо поддержки постоянно меняющихся данных должна быть возможность обхода элементов коллекции в отсортированном порядке [2].
При выборе подходящего алгоритма не стоит забывать о стоимости предварительной обработки структур данных, которая может потребоваться алгоритму до начала выполнения поисковых запросов. Стоит выбирать подходящую структуру данных, которая не только ускоряет производительность отдельных запросов, но и сводит к минимуму общую стоимость поддержания структуры коллекции в условиях динамического доступа и многократных запросов.
Также стоит обращать внимание на то, что в коллекции могут иметься повторяющиеся значения, и поэтому ее нельзя рассматривать как множество (в котором не допускается наличие одинаковых элементов).
Учитывая, что все поставленные задачи курсовой работы решены, можно обоснованно утверждать, что главная цель исследования – достигнута.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
- Джордж Хайнеман, Гэри Пояяис, Стэняи Сеяков. Алгоритмы. Справочник с примерами на С, C++, Java и Python – 2017 [120-155]
- Готтшлинг П. - C++ для инженерных и научных расчетов (C++ In-Depth) – 2020 [159-163]
- Шлее М. - Qt 5.10. Профессиональное программирование на C++ (В подлиннике) – 2018 [91-95]
- Страуструп Б. - Язык программирования С++. Краткий курс – 2019 [211-219]
- Васильев А.Н. - Программирование на C++ в примерах и задачах (Российский компьютерный бестселлер) – 2017 [73-88]
Интернет ресурсы:
- https://codelessons.ru/cplusplus/algoritmy/linejnyj-poisk-po-massivu-c.html
- https://codelessons.ru/cplusplus/algoritmy/binarnyj-poisk-po-massivu-c.html
- https://proglib.io/p/must-have-algoritmy-dlya-raboty-so-strokami-na-c-2020-03-30
- https://habr.com/ru/company/ua-hosting/blog/281517/
- https://algor.skyparadise.org/read/7
ПРИЛОЖЕНИЯ
Приложение А
Последовательный поиск. Листинг.
#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;
int main() {
setlocale(LC_ALL, "rus");
int ans[20]; // создали массив для записи всех индексов
int h = 0;
int arr[20]; // создали массив на 20 элементов
int key; // создали переменную в которой будет находиться ключ
srand ( time(NULL) );
for (int i = 0; i < 20; i++) {
arr[i] = 1 + rand() % 20; // заполняем случайными числами ячейки
cout << arr[i] << " "; // выводим все ячейки массива
if (i == 9) {
cout << endl;
}
}
cout << endl << endl << "Введите ключ : "; cin >> key; // считываем ключ
for (int i = 0; i < 20; i++) {
if (arr[i] == key) { // проверяем равен ли arr[i] ключу
ans[h++] = i;
}
}
if (h != 0) { // проверяем были ли совпадения
for (int i = 0; i < h; i++) {
cout << "Ключ " << key << " находится в ячейке " << ans[i] << endl; //выводим все индексы
}
}
else {
cout << "Мы не нашли ключ " << key << " в массиве";
}
system("pause");
return 0;
}
Приложение Б
Бинарный поиск. Листинг.
#include <iostream>
#include <algorithm>
using namespace std;
int main() {
setlocale(LC_ALL, "rus");
int arr[10]; // создали массив на 10 элементов
int key; // создали переменную в которой будет находиться ключ
cout << "Введите 10 чисел для заполнения массива: " << endl;
for (int i = 0; i < 10; i++) {
cin >> arr[i]; // считываем элементы массива
}
sort (arr, arr + 10); // сортируем с помощью функции sort (быстрая сортировка)
cout << endl << "Введите ключ: ";
cin >> key; // считываем ключ
bool flag = false;
int l = 0; // левая граница
int r = 9; // правая граница
int mid;
while ((l <= r) && (flag != true)) {
mid = (l + r) / 2; // считываем срединный индекс отрезка [l,r]
if (arr[mid] == key) flag = true; //проверяем ключ со серединным элементом
if (arr[mid] > key) r = mid - 1; // проверяем, какую часть нужно отбросить
else l = mid + 1;
}
if (flag) cout << "Индекс элемента " << key << " в массиве равен: " << mid;
else cout << "Извините, но такого элемента в массиве нет";