ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.10.2024
Просмотров: 61
Скачиваний: 0
СОДЕРЖАНИЕ
Методика обработки полной информации
2. Составление статистического ряда
3. Определение среднего значения показателя надёжности и среднего квадратичного отклонения
4. Проверка информации на выпадающие точки
5. Выполнение графического изображения опытного распределения показателя надежности
6. Определение коэффициента вариации
7. Выбор теоретического закона распределения для выравнивания опытной информации
7.1. Использование для выравнивания распределения опытной информации знр
7.2. Использование для выравнивания распределения опытной информации зрв
9. Определение доверительных границ рассеивания одиночного и среднего значения показателя надёжности
9.1.Определение доверительных границ рассеивания при законе нормального распределения
9.2.Определение доверительных границ при законе распределения Вейбулла

|
|

Оглавление
Методика обработки полной информации 3
1.Составление сводной таблицы информации в порядке возрастания показателя надежности 3
2. Составление статистического ряда 4
3. Определение среднего значения показателя надёжности и среднего квадратичного отклонения 5
4. Проверка информации на выпадающие точки 6
5. Выполнение графического изображения опытного распределения показателя надежности 7
6. Определение коэффициента вариации 9
7. Выбор теоретического закона распределения для выравнивания опытной информации 10
8. Оценка совпадений опытного и теоретического законов распределения показателя надежности по критерию согласия Пирсона 18
9. Определение доверительных границ рассеивания одиночного и среднего значения показателя надёжности 21
10. Определение абсолютной и относительной предельных ошибок переноса опытных характеристик показателя надёжности 25
Список литературы 27
Методика обработки полной информации
Составление сводной таблицы информации в порядке возрастания показателя надежности
Таблица 1 – Информации о доремонтных ресурсах двигателя
|
1 |
1124 |
|
2 |
1212 |
|
3 |
1320 |
|
4 |
1350 |
|
5 |
1480 |
|
6 |
1540 |
|
7 |
1620 |
|
8 |
1620 |
|
9 |
1670 |
|
10 |
1670 |
|
11 |
1900 |
|
12 |
1950 |
|
13 |
1970 |
|
14 |
1980 |
|
15 |
2010 |
|
16 |
2070 |
|
17 |
2190 |
|
18 |
2220 |
|
19 |
2290 |
|
20 |
2300 |
|
21 |
2370 |
|
22 |
2440 |
|
23 |
2600 |
|
24 |
2820 |
|
25 |
2960 |
|
26 |
3150 |
|
27 |
3400 |
|
28 |
3720 |
2. Составление статистического ряда
Для упрощения дальнейших расчетов составляется статистический ряд
Когда N>25 составляется статистический ряд. В данном примере N=28 целесообразно составить статистический ряд
Информация
разбивается на интервалы. Число интервалов
n=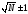 ,
,
где
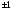 означает округление до ближайшего
большого целого числа.
означает округление до ближайшего
большого целого числа.
В
нашем примере n=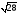 =6.
Принимаем число интерваловn=6
=6.
Принимаем число интерваловn=6
Длина интервалов
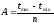 ,
(2.1)
,
(2.1)
где
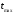 ,
,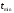 - наибольшее и наименьшее значение
показателя надежности в сводной таблице
1.
- наибольшее и наименьшее значение
показателя надежности в сводной таблице
1.
Таблица 2 – Статистический ряд
|
Интервал, тыс. мото-ч |
1124-1556,7 |
1556,7-1989,3 |
1989,3-2422 |
2422-2854,7 |
2854,7-3287,3 |
3287,3-3720 |
|
Опытная частота, mi |
6 |
8 |
7 |
3 |
2 |
2 |
|
Опытная вероятность, Pi |
0,21 |
0,29 |
0,25 |
0,11 |
0,07 |
0,07 |
|
Накопленная опытная вероятнсть |
0,21 |
0,50 |
0,75 |
0,86 |
0,93 |
1,00 |
Определение опытной вероятности
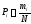 ,
(2.2)
,
(2.2)
где
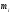 - опытная частота в i-том
интервале статистического ряда;
- опытная частота в i-том
интервале статистического ряда;
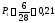
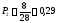

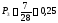
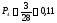
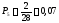
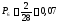

Определение накопленной опытной вероятности
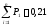
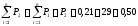
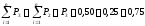
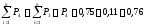
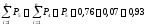
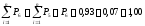
3. Определение среднего значения показателя надёжности и среднего квадратичного отклонения
При наличии статистического ряда когда N>25 находим по формуле
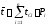 , (3.1)
, (3.1)
где tci – значение середины i-го интервала
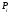 -
опытная вероятность i-го
интервала
-
опытная вероятность i-го
интервала
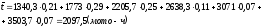
Определение квадратического отклонения – характеризуется рассеиванием среднего значения показателя надежности
При N>25 определяется по формуле
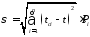 (3.2)
(3.2)

4. Проверка информации на выпадающие точки
Грубую
проверку выполняют по правилу
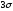 :
:
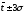 ,
(4.1)
,
(4.1)
Нижняя граница будет равна
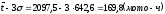
Верхняя граница будет равна
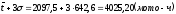
Наименьший
доремонтный ресурс двигателя
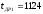 мотто-ч. Следовательно, эта точка
информации действительна и должна быть
учтена в дальнейших расчетах. Наибольший
ресурс двигателя
мотто-ч. Следовательно, эта точка
информации действительна и должна быть
учтена в дальнейших расчетах. Наибольший
ресурс двигателя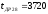 мото-ч.
Эта точка информации действительна и
должна быть учтена в дальнейших расчетах.
мото-ч.
Эта точка информации действительна и
должна быть учтена в дальнейших расчетах.
Проверка по критерию Ирвина
Фактическое значение критерия
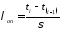 ,
(4.2)
,
(4.2)
где ti и t(i-1)смежные точки информации
При λоп≤ λт-точка является действительной
При λоп≥ λт-точка является выпадающей
В данном примере
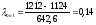
Верхняя граница :
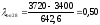
По таблице №4 методички находим, что при β=0,95 и N=28, λт=1,2

Первая точка информации является действительной т.к λоп1=0,14≤ λт=1,2
Последняя точка информаций также является действительной т.к λоп28=0,50≤ λт=1,2