Файл: Gidravlika_ekzamen.docx

Для расширения диапазона измеряемых давлений рекомендуется давление жидкости уравновешивать жидкостью большего удельного веса. Обычно такой жидкостью является ртуть, т.к. γ_рт>γ_вв 13,6 раза, поэтому при измерении одних и тех же давлений трубка оказывается значительно короче пьезометрической и прибор получается более компактный. Такой прибор называют ртутным манометром.

Ртутный манометрпредставляет собойU-образную стеклянную трубку, изогнутое колено которой заполнено ртутью, один колец трубки соединен с областью, в которой необходимо измерить давление, а другой – открытый. До подключения манометра ртуть находиться в обоих коленах на одном уровне. Если в резервуаре давление манометрическое, то уровень ртути в левом колене понизиться, а в правом – повыситься, при этом равновесие наступит в тот момент, когда наступит равенство давлений на горизонтальной поверхности равного давления. Абсолютное давление

p_А= p_атм+γ_ртh_рт

Абсолютное давление в точке подключения манометра

p= p_атм+γ_ртh_рт –γh₁

Если в резервуаре давление pвакуметрическое, то после подключения ртутного манометра в левом колене в левом колене поднимется, а в правом понизится. На свободной поверхности ртути p_атм= p+γ_ртh_рт откуда p= p_атм- γ_ртh_{рт .} В этом случае вакуумp_вак= γ_ртh_рт.

Высоту h_рт=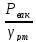 , соответствующей вакууму в резервуаре (p_вак=p_атм-p) называют вакуумметрической высотой .Таким образом, вакуум также можно измерить по высоте столба рабочей жидкости.

Батарейный двухжидкостный манометр применяют для увеличения диапазона измеряемых давлений. Прибор состоит из двух-трех колен соединенных между собой U-образных трубок, нижняя часть которых заполнена ртутью, а верхняя – той же жидкостью, что и в резервуаре, в котором измеряется давление. В зависимости от того, какое давление жидкости в резервуаре – манометрическое или вакуумметрическое, уровни ртути и жидкости в коленах соответствующим образом уравновеситься: в случае манометрического (избыточного) - в левом колене уровень ртути понизиться, а в правом – поднимется; соответственно при вакуумметрическом давлении в левом колене – поднимется, а в правом - понизиться.

Расчет величины избыточного для вакуумметрического давления в точке К подключения прибора начинают от открытого конца трубки с учетом понятия поверхности равного давления: во всех точках горизонтальной плоскости, проведенной в однородной жидкости, гидростатические давления одинаковы, т.е.

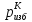= γ_рт*(h₅-h₄)-γ*(h₃-h₂)+γ_рт*(h₃-h₂)-γ*(h₁-h₂) Дифференциальный манометр применяют для измерения разности давлений в двух резервуарах или в двух точках жидкости в одном и том же резервуаре.

Наиболее часто применяются дифференциальные ртутные манометры, состоящие из двух соединенных между собой стеклянных U-образных трубок.

Обозначив через p₁и p₂ давление в первом и втором резервуарах, h₁и h₂ - высоты столбиков жидкости в среднем колене над уровнем ртути, h_рт – разность уровней ртути, получим следующее уравнение равновесия давления на уровне поверхности ртути в левом колене

p₁+γh₁₌ p₂+γh₂++γ_ртh_рт

откуда

p₁- p₂=γh₂-γh₁+γ_ртh_рт

Но так как h₂-h₁₌-h_рт, то p₁- p₂= h_рт *(γ_рт - γ)

Таким образом, разность давлений определяется произведением рабочего столбика ртути на разность удельных весов ртути и жидкости в резервуарах. Если в резервуарах жидкости разной плотности, то при составлении уравнения равновесия должны быть учтены соответствующие значения удельных весов.

8. Гидростатический напор. Показать на чертеже сосуда с жидкостью и пьезометрами гидростатический напор и его составляющие части.

Гидростатический напор H— это энергетическая характеристика покоящейся жидкости. Напор измеряется в метрах по высоте (вертикали).

Гидростатический напор Hскладывается из двух величин

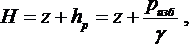
где z— геометрический напор или высота точки над нулевой горизонтальной плоскостью отсчёта напора 0-0;h_p — пьезометрический напор (высота).

Гидростатический напор Hхарактеризует потенциальную энергию жидкости (энергию покоя). Его составляющаяzотражает энергию положения. Например, чем выше водонапорная башня, тем больший напор она обеспечивает в системе водопровода. Величинаh_pсвязана с давлением. Например, чем выше избыточное давление в водопроводной трубе, тем больше напор в ней и вода поднимется на бóльшую высоту.

Напоры для различных точек жидкости надо отсчитывать от одной горизонтальной плоскости 0-0 для того, чтобы их можно было сравнивать друг с другом. В качестве горизонтальной плоскости сравнения 0-0 может быть принята любая. Однако, если сама труба горизонтальна, то иногда для упрощения расчётов удобнее 0-0 провести по оси трубы. Тогда геометрическая высота z обратится в ноль.

Важная особенность гидростатического напора состоит в том, что он одинаков для всех точек покоящейся жидкости, гидравлически взаимосвязанных.

9. Определение силы давления жидкости на плоскую фигуру произвольной формы и точки ее приложения.

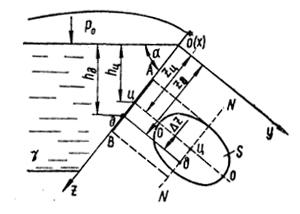
Полная сила давления жидкости на плоскую фигуру ABпроизвольной формы (см. рисунок) определяется по формуле

P_полн = (p₀ + γ·h_c)·w = p_с·w,

где p₀- гидростатическое давление на свободной поверхности жидкости в резервуаре; γ - удельный вес жидкости;w- площадь фигуры;h_ц- глубина погружения центра тяжести смоченной поверхности фигуры;p_c- гидростатическое давление в центре тяжести фигуры.

Таким образом, полная сила давления жидкости на плоскую фигуру равна произведению площади этой фигуры и гидростатическому давлению в ее центре тяжести.

Вышеприведенное выражение можно представить в виде:

P_полн = P₀ + P,

где,

P₀ = p₀·w;

P =γ·h_c·w.

Сила P₀представляет собой силу поверхностного давления, обусловленную наличием давления на свободной поверхности жидкости в сосуде. Точка приложения этой силы совпадает с центром тяжести фигуры (на рисунке точкаc).

Сила Рназывается силой избыточного давления. Она обусловлена давлением самой жидкости непосредственно на рассматриваемую фигуру и определяется весом столба жидкости, основанием которого является площадьwфигуры, а высотой - глубина погружения центра тяжести фигуры в жидкостьh_c. Последним выражением определяется сила избыточного давления и в том случае, когда резервуар открыт и поверхностным давлением является давление атмосферы.

Положение точки приложения силы Р(на рисунке точкад) определяется по формуле:

y_д = y_c + I_c/(w·y_c)

где y_д- ордината точки приложения силы избыточного давления, отсчитываемая в плоскости фигуры от свободной поверхности жидкости (по осиоу); у_с- ордината центра тяжести площадиw;y_c- момент инерции площади фигуры относительно горизонтальной осио-о, лежащей в плоскости фигуры и проходящей через ее центр тяжести (так называемый центральный момент инерции).

Точка приложения силы избыточного давления расположена ниже (считая по стенке) центра тяжести смоченной поверхности фигуры на величину Δz, определяемую выражениемΔz = I_ц/(wy_c)

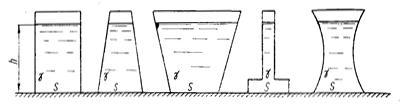
Сила давления на горизонтальное дно сосуда зависит от рода жидкости γ, глубины жидкости в сосудеhи площади днаS и не зависит от формы сосуда. Таким образом, если в сосуды разной формы, но с одинаковой площадью дна налита одинаковая жидкость на одну и ту же глубину, то сила давления на дно сосуда будет одинаковой и равнойP = γ·h_ц·S. В этом и заключаетсягидростатический парадокс.

10. Построение эпюр гидростатического давления жидкости на плоские и ломанные стенки.

Давление жидкости на плоскую наклонную стенку

Пусть мы имеем резервуар с наклонной правой стенкой, заполненный жидкостью с удельным весом γ. Ширина стенки в направлении, перпендикулярном плоскости чертежа (от читателя), равна b Стенка условно показана развернутой относительно оси АВ и заштрихована на рисунке. Построим график изменения избыточного гидростатического давления на стенку АВ.

Так как избыточное гидростатическое давление изменяется по линейному закон P=γgh, то для построения графика, называемого эпюрой давления, достаточно найти давление в двух точках, например А и B.

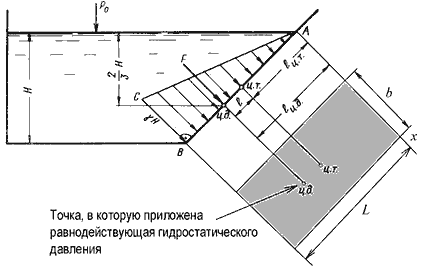
Избыточное гидростатическое давление в точке А будет равно

P_A = γh = γ·0 = 0

Соответственно давление в точке В:

P_B = γh = γH

где H - глубина жидкости в резервуаре.

Согласно первому свойству гидростатического давления, оно всегда направлено по нормали к ограждающей поверхности. Следовательно, гидростатическое давление в точке В, величина которого равна γH, надо направлять перпендикулярно к стенке АВ. Соединив точку А с концом отрезка γH, получим треугольную эпюру распределения давления АВС с прямым углом в точке В.

Среднее значение давления будет равно

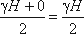
Если площадь наклонной стенки S=bL, то равнодействующая гидростатического давления равна

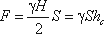
где hc = Н/2 - глубина погружения центра тяжести плоской поверхности под уровень жидкости.

Однако точка приложения равнодействующей гидростатического давления ц.д. не всегда будет совпадать с центром тяжести плоской поверхности. Эта точка находится на расстоянии l от центра тяжести и равна отношению момента инерции площадки относительно центральной оси к статическому моменту этой же площадки.

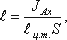
где J_Аx - момент инерции площади S относительно центральной оси, параллельной Аx.

11. Определение силы гидростатического давления на произвольную криволинейную поверхность.