ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.10.2024
Просмотров: 139
Скачиваний: 0
СОДЕРЖАНИЕ
Давление жидкости на плоскую наклонную стенку
Вывод уравнения Бернулли для установившегося, плавноизменяющегося потока жидкости.
9) Способы регулирования подачи центробежных насосов.
1.Водоснабжение – как отрасль народного хозяйства. Классификация систем водоснабжения.
2) Схема водоснабжения с забором из поверхностного водоисточника.
3) Схема водоснабжения с забором из подземного водоисточника.
4) Производительность и напор водопроводных насосных станций I и II подъема.
6) Определение высоты водонапорной башни.
7) Определение регулирующей емкости бака водонапорной башни.
8) Автоматический безбашенная водоподъемная установка. Схема и принцип действия.
9) Водоструйный водоподъемник, схема и принцип действия.
10) Воздушный водоподъемник (эрлифт), схема и принцип действия.
11) Требования, предъявляемые к источнику водоснабжения.
Вывод уравнения Бернулли для установившегося, плавноизменяющегося потока жидкости.
Z1+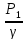 +
+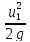 = Z2+
= Z2+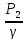 +
+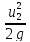 +hL
+hL
(Z1+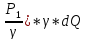 +
+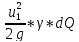 = (Z2+
= (Z2+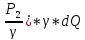 +
+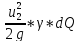 +hL
+hL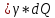
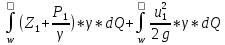 =
=
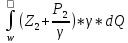 +
+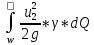 +
+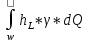
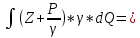
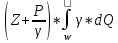 =
=
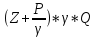
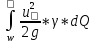 =
=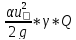
α – учитывается неравномерность распределения скорости по живому сечению потоку.
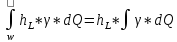 =
=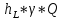
(Z1+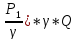 +
+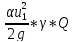 = (Z2+
= (Z2+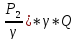 +
+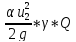 +hL
+hL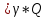
Z1+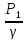 +
+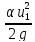 = Z2+
= Z2+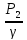 +
+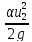 + hL
+ hL
Виды существующих потерь напора
hL – потери напора по длине
hмп – местные потери напора
hL + hмп = hw – полные потери
Z1+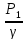 +
+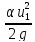 =Z2+
=Z2+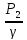 +
+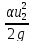 +hw
+hw
Написать уравнение Бернулли для потока в общем виде и в следующих частных случаях: напорное равномерное движение; напорное равномерное движение по горизонтальной трубе; безнапорное равномерное движение.
Написать уравнение Бернулли для потока в общем виде
Z1+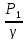 +
+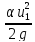 = Z2+
= Z2+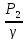 +
+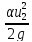 + hw
+ hw
Частных случаи:
Напорное равномерное движение:
υ1= υ2
Z1+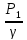 =Z2+
=Z2+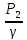 +hL
+hL
Напорное равномерное движение по горизонтальной трубе:
υ1= υ2 Z1= Z2
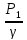 =
=
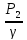 +hL
+hL
Безнапорное равномерное движение:
υ1= υ2 p1= p2=pатм
Z1 =
Z2
=
Z2 + hL
+ hL
Режимы движения жидкости. Число Рейнольдса и его критическое значение. Зачем при расчете гидравлических сиситем нужно знать режим движения жидкости.
Режимы движения жидкости.
Ламинарный – режим, при котором частицы жидкости движутся по траекториям параллельным стенкам трубы без перемешивания и обмена частицам между струйками.
Турбулентный – режим характеризуется беспорядочными, хаотическим движением частиц, сопровождающимся перемешиванием жидкости по всему сечению потока при общем направленном движении.
Число Рейнольдса и его критическое значение.
Числом Рейнольдса Re называют безразмерный параметр, зависящий от скорости, характерного линейного размера живого сечения и вязкости жидкости.
Для напорной трубы круглого сечения число Рейнольдса
Re
=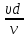
Критическое число Рейнольдса Reкр соответствует переходу из одного режима в другой. Для круглых напорных труб критическое число Рейнольдса Reкр =2320
При Re < Reкр наблюдается ламинарный режим движения, при Re > Reкр – турбулентный. При значениях Re близких к Reкр ,существует область неустойчивых режимов движения.
Зачем при расчете гидравлических сиситем нужно знать режим движения жидкости.
Зная число Рейнольдса, мы можем определить режим движения жидкости, который в дальнейшем нам понадобиться для определения коэффициента гидравлического трения.
Формула Дарси. Определение потерь напора на трение при напорном движении в круглых трубах в зависимости от режима движения.
|
Зона области |
Число Re |
Режим движения |
Коэффициент λ |
Расчетная формула |
Характер связи между hL и υ |
|
Зона ламинарного движения |
Re < Reкр |
Ламинарный |
λ= |
hL
=
hL
=λ*
|
hL=k*υ |
|
Зона турбулентного режима жидкости при Re > Reкр |
|||||
|
Область гидравлически гладких труб |
Reкр< Re < ReIпр |
Турбулентный |
λ= |
hL
=λ*
|
hL=k*υ1,75 |
|
Область доквадратического сопротивления (переходная) |
ReIпр < Re < ReIIпр |
Турбулентный |
λ=0,11*(∆r+ |
hL
=λ*
|
hL=k*υ(1,75…2) |
|
Область квадратического сопротивления |
Re < ReIIпр |
Турбулентный |
λ=0,11*∆r0,25 |
hL
=λ*
|
hL=k*υ2,0 |
Относительная шероховатость
∆r=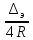 =
=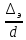
 -
эквивалентная
шероховатость
-
эквивалентная
шероховатость
Первое предельное число Re
ReIIпр
=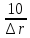
Второе предельное число Re
ReIIпр
=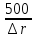
Местные потери напора. Их возникновение, виды и способы определения.
Местные сопротивления представляют собой короткие фасонные участки трубопроводов (вход в трубу, задвижки, вентиль, колено, клапан, тройник и т.д.), которые вызывают деформацию потока и являются причиной дополнительных потерь напора. В результатах измерения размеров и формы сечения или направления продольной оси изменяются величина и направление скорости потока, происходит интенсивное вихреобразование в связи с отрывом потока от ограничивающих его стенок, на что затрачивается дополнительная энергия.
Потери удельной энергии потока на преодоление местных сопротивлений выражается в линейных единицах измерения удельной энергии, и называются местными потерями напора.
Величина местных потерь напора определяется по общей формуле Вейчбаха:
hм=ξ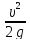
ξ – безразмерный коэффициент местных сопротивлений.
Из уравнения Бернулли, записанного для сечений, расположенных до и после местного сопротивления, получаем:
hм
= (Z1+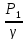 +
+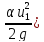 – (Z2+
– (Z2+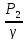 +
+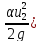
При внезапном расширение:
ξ=(1-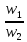 )2
или
ξ=
)2
или
ξ=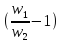
hм=
ξ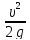
w1= площадь сечения до расширения
w2= площадь сечения после расширения.
При внезапном сужение:
ξ=0,5(1-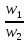 )
)
w1= площадь сечения до сопротивления
w2= площадь сечения после сопротивления
Выход из трубы в неподвижную жидкость:
w1>> w2 υ2~0 => ξ~1
При входе в трубку с острыми кромками из резервуара.
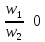 ξ=0,5(1-
ξ=0,5(1-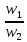 )
ξ~ 0,5
)
ξ~ 0,5
Плавный поворот трубы на 90о
ξ=0,051+0,19
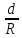
Внезапное сужение или внезапное расширение горизонтального трубопровода, скорости в широком и узком сечениях различны, поэтому потери напора в этих случаях равны:
hм
= (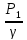 +
+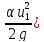 – (
– (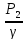 +
+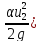
Горизонтальный участок трубопровода постоянного сечения, то потери напора будет равна разности показаний пьезометров, установленных в сечениях перед и за местными сопротивлениями в местах, где на поток не сказывается возмущение, налагаемое сопротивлением:
υ1= υ2 Z1= Z2
hм
=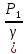 -
-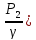
Местное сопротивление, расположенное на вертикальном участке трубопровода постоянного диаметра:
hм
= (Z1+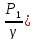 – (Z2+
– (Z2+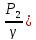
Внезапное сужение или внезапное расширение на вертикальном трубопровода:
hм
= (Z1+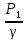 +
+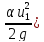 – (Z2+
– (Z2+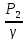 +
+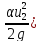
Гидравлический расчет коротких трубопроводов. Типы решаемых задач. Выбор сечений для составления уравнения Бернулли.
Коротким называется трубопровод при расчете которого учитывают оба вида потерь напора, т.к. в общем, баланс потерь, местные потери сопоставимы с потерями по длине:
hw=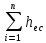 +
+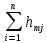
Основным уравнением и зависимости используемые при расчете трубопровода:
Уравнение Бернулли
Z1+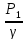 +
+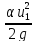 = Z2+
= Z2+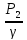 +
+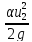 +hм
+hм
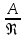
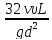
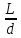 *
*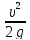
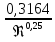
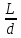 *
*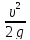
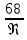 )0,25
)0,25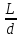 *
*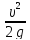
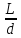 *
*