Файл: Методы кодирования данных ( СУЩНОСТЬ КОДИРОВАНИЯ ИНФОРМАЦИИ ).pdf

Наиболее распространенными в настоящее время позици­онными системами счисления являются десятичная, двоич­ная, восьмеричная и шестнадцатеричная. Каждая позицион­ная система имеет определенный алфавит цифр и основание.

В позиционных системах счисления основание системы равно количеству цифр (знаков в ее ал­фавите) и определяет, во сколько раз различают­ся значения одинаковых цифр, стоящих в сосед­них позициях числа.

Десятичная система счисления имеет алфавит цифр, кото­рый состоит из десяти всем известных, так называемых араб­ских, цифр, и основание, равное 10, двоичная — две цифры и основание 2, восьмеричная — восемь цифр и основание 8, шестнадцатеричная — шестнадцать цифр (в качестве цифр используются и буквы латинского алфавита) и основание 16.

Таблица 1.1

Позиционные системы счисления

Двоичная система счисления. В двоичной системе счисле­ния основание равно 2, а алфавит состоит из двух цифр (0 и 1). Следовательно, числа в двоичной системе в развернутой форме записываются в виде суммы степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1. [10, с.47]

Любое неотрицательное число в позиционной системе счисления может быть представлено в виде:

,

где а - основание системы счисления,

хi - разряды (числа от 0 до а-1), их обозначения образуют алфавит системы счисления,

аi - весовые коэффициенты (веса) разрядов,

n - число разрядов целой части числа,

р - число разрядов дробной части числа.

Например, число в десятичной системе счисления 57310=5*102+7*101+3*100

Число в двоичной системе счисления:

Позиционная система счисления - такая, в которой весовые коэффициенты определяются позицией разряда.

В вычислительной технике наиболее распространены: двоичная (binary, BIN), десятичная (decimal, DEC), шестнадцатеричная (hexadecimal, HEX) и непозиционная двоично-десятичная (binary coded decimal, BCD) системы исчисления. В BCD системе вес каждого разряда равен степени 10, как в десятичной системе, а каждая цифра i-го разряда кодируется 4-мя двоичными цифрами. Восьмеричная система счисления (octal, OCT) применяется реже. Следует отметить, что в цифровые устройства используют только двоичную систему счисления, так как построены на основе устройств с двумя состояниями. Другие системы счисления используются человеком только для удобства записи, т.е. для сокращенного (и часто более удобного) представления двоичных чисел.

Формат двоичного числа

Микропроцессоры обрабатывают упорядоченные двоичные наборы. Минимальной единицей информации является один бит (BInary digiT).

Далее следуют – тетрада, или ниббл (4 бита), байт ( byte, 8 бит), двойное слово (DoubleWord 16 бит) или длинное (LongWord 16 бит) и учетверенное (32 бита) слова. Младший бит обычно занимает крайнюю правую позицию, старший - соответственно крайнюю левую, т.е. “старшинство” разрядов убывает слева направо.

Шестнадцатеричное представление двоичных чисел. Для перевода числа из двоичной системы в шестнадцатеричную, его необходимо разбить, начиная справа на тетрады - группы по 4 двоичных цифры - и каждую группу представить шестнадцатеричной цифрой из таблицы. Для обратного перевода каждая HEX цифра заменяется четверкой двоичных, незначащие нули слева иногда (но не всегда) отбрасываются. Нуль обычно не отбрасывается, если старший значащий знак обозначен буквой (см. таблицу).

Таблица 1.2

Двоичные и шестнадцатиричные (HEX) коды целых чисел от 0 до 15

Пример: число 57310 = 10001111012 = 023D16 = 023Dh

Вывод по 1 главе

Для автоматизации работы с данными, относящимися к различным типам используется приём кодирования, т.е. выражение данных одного типа через данные другого типа.

Мы в своей работе будем опираться на следующее определение: «Код (code) – это совокупность знаков, символов и правил представления информации».

Сигналы, реализующие коды, обладают одной из следующих характеристик:

• • униполярный код (значения сигнала равны 0, +1, либо 0, -1 );
  • полярный код (значения сигнала равны +1, -1);
  • биполярный код (значения сигнала равны 0, +1, -1).

Последовательным является такой код, в котором знаки следуют один за другим во времени. Параллельным – тот, в котором знаки передаются одновременно, образуя символ.

Естественные языки обладают большой избыточностью, поэтому для экономии памяти, объем которой ограничен, имеет смысл ликвидировать избыточность текста или уплотнить текст.

Существуют несколько способов уплотнения текста.

• 1. Переход от естественных обозначений к более компактным.
  2. Подавление повторяющихся символов.
  3. Кодирование часто используемых элементов данных.
  4. Посимвольное кодирование.
  5. Коды переменной длины.

Информация передается в виде сообщений. Дискретная информация записывается с помощью некоторого конечного набора знаков, которые называются буквами. Буква в данном расширенном понимании - любой из знаков, которые некоторым соглашением установлены для общения.

В канале связи сообщение, составленное из символов (букв) одного алфавита, может преобразовываться в сообщение из символов (букв) другого алфавита. Саму процедуру преобразования сообщения называют перекодировкой.

Для записи информации о количестве объектов использу­ются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисле­ния.

Все системы счисления делятся на две большие группы: позиционные и непозиционные системы счисления. Самой рас­пространенной из непозиционных систем счисления являет­ся римская. Наиболее распространенными в настоящее время позици­онными системами счисления являются десятичная, двоич­ная, восьмеричная и шестнадцатеричная.

Первая позиционная система счисления была придумана еще в Древнем Вавило­не, в XIX веке довольно широкое распространение получи­ла двенадцатеричная система счисления. В настоящее время человечество приняло в использование десятеричную систему счисления.

В позиционных системах счисления количествен­ное значение цифры зависит от ее позиции в числе. Перевод из одной систему счисления в другую производится с помощью определенных правил, а в частности для двоичных, восьмеричных и шестнадцатеричных с использованием триад и тетрад, обеспечивающих удобство перевода.

ГЛАВА 2.КОДИРОВАНИЕ ИНФОРМАЦИИ В СИСТЕМЕ ОБРАБОТКИ ИНФОРМАЦИИ

2.1. Кодирование текстовой информации

В процессе обработки информации, т.е. преобразова­ния информации из одной формы представления (зна­ковой системы) в другую осуществляется кодирование. Средством кодирования служит таблица соответствия, которая устанавливает взаимно однозначное соответ­ствие между знаками или группами знаков двух раз­личных знаковых систем. При вводе знака алфавита в компьютер путем нажатия соответствующей клавиши на клави­атуре выполняется его кодирование, т. е. преобразо­вание в компьютерный код. При выводе знака на эк­ран монитора или принтер происходит обратный про­цесс — декодирование, когда из компьютерного кода знак преобразуется в графическое изображение.

Текст состоит из символов, поэтому символ можно считать минимальным элементом текста. Если собрать все возможные символы, которые могут встретиться в тексте: латинские буквы, буквы кириллицы, знаки пре­пинания и т. д., и каждому из этих символов присвоить свой уникальный номер (код символа), то текст можно записать в виде набора чисел.

Для хранения кода одного символа может быть вы­делен один байт. С помощью одного байта можно зако­дировать 256 различных символов, учитывая, что каж­дый бит принимает значение 0 или 1, и количество их возможных сочетаний в байте равно 2⁸=256. Этого вполне достаточно для представления текстовой инфор­мации, включая прописные и строчные буквы русского и латинского алфавитов, цифры, знаки, псевдографиче­ские символы и т. д [19, с.24].

Кодирование заключается в том, что каждому сим­волу ставится в соответствие уникальный десятичный код от 0 до 255 или соответствующий ему двоичный код от 00000000 до 11111111. Таким образом, человек разли­чает символы по их начертанию, а компьютер — по их коду. Важно, что присвоение символу конкретного ко­да — это вопрос соглашения, которое фиксируется в ко­довой таблице.

Технически это выглядит очень просто, однако всегда существовали достаточно веские организационные сложности. В первые годы развития вычислительной техники они были связаны с отсутствием необходимых стандартов, а в настоящее время вызваны, наоборот, изобилием одновременно действующих и противоречивых стандартов. Для того чтобы весь мир одинаково кодировал текстовые данные, нужны единые таблицы кодирования, а это пока невозможно из-за противоречий между символами национальных алфавитов, а также противоречий корпоративного характера.

Существует несколько различных стандартов коди­рования символов, но первоосновой для всех стал стандарт ASCII (American Standard Code for Information In­terchange — американский стандартный код для инфор­мационного обмена).

В ASCII закреплены две таблицы кодирования: ба­зовая и расширенная. В базовой таблице определены значения кодов с 0 по 127, а в расширенной — с 128 по 255. В базовой таблице находятся символы латинского алфавита, цифры, знаки арифметических операций и знаки препинания (табл. 1.1). Кроме того, за кодами с 0 по 32 закреплены специальные функции: перевод стро­ки, ввод пробела и т. д. Расширенная таблица содержит символы национальных алфавитов различных стран мира и так называемые символы псевдографики, с по­мощью которых можно, например, рисовать таблицы [19, с.25].

Рис.2.1 Таблица кодов ASCII (расширенная)

Для языков, использующих кириллицу, в том числе и для русского, пришлось полностью менять вторую полови­ну таблицы ASCII, приспосабливая её под кириллический алфавит. В частности, для представления символов ки­риллицы используется так называемая «альтернативная кодировка».

Альтернативная кодировка не подошла для ОС Windows. Пришлось передвинуть русские буквы в таб­лице на место псевдографики, и получили кодировку Windows 1251 (Win-1251). Кодировка символов русского языка, известная как кодировка Windows-1251, была введена «извне» - компанией Microsoft, но, учитывая широкое распространение операционных систем и других продуктов этой компании в России, она глубоко закрепилась и нашла широкое распространение.

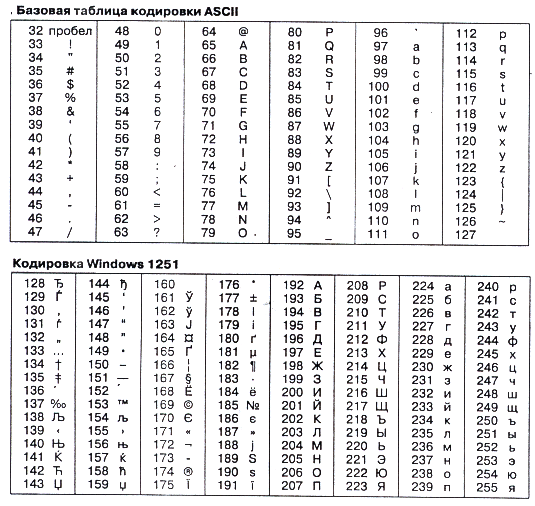
Сейчас существует несколько различных кодовых таблиц для русских букв (КОИ-8, СР-1251, СР-866, Мае, ISO), причём тексты, созданные в одной кодировке, мо­гут совершенно неправильно отображаться в другой. Решается такая проблема с помощью специальных про­грамм перевода текста из одной кодировки в другую [4. c.67].