Файл: Лабораторный практикум В. Ф. Говердовский, А. В. Дикинис.pdf

II. Длинноволновое уходящее (земное)  излучение

1. 

Безоблачная атмосфера. Восходящая радиация определяется 

соотношением:

т

F ](z)

 = 

0

 I4п рд

( М -  mz) +

 J 

а  I

4

 фд(м - 

mz),

(6.32)

м

а нисходящая радиация вычисляется по формуле:

щ

F l(z)

 = j"o 

I

4

 dpn(mz - u

) 

(6.33)

о

2.  Подоблачный слой.  Восходящая радиация рассчитывается 

как  в  случае  безоблачной  атмосферы,  по  соотношению  (6.32), 

а нисходящая - по соотношению:

щ

F i

 (z) = a 

f

nT0

 рд 

(mz-  mmo)

 +  |  о Т4 

dpa(mz 

-  и)

  (6.34)

тлЯ

3. Надоблачный слой. Восходящая радиация равняется

т ,

F'\(z) = <

5

l ANoPa(.mmo- m ^ +

j  

о 

I

4

фд(и - 

т2),

  (6.35)

тААГ

Нисходящая радиация определяется так же, как при безоблач­

ной атмосфере, то есть выражением (6.33).

В  формулах  (6.32)-(6.35)  используются  обозначения: 

а  = 

5,67-10-8  Вт/(м2-К4)  =  0,816-ДО-10  кал/(мин-см2-К4)  -  постоянная 

Стефана-Больцмана; 

Тп

 - температура подстилающей земной по­

верхности;  Гвго и  Гнго - соответственно температура на верхней и 
нижней границах облачности; 

Т -

 температура на уровне 

m

(

z

) ; 

па­

раметр интегрирования 

и

 меняется в интервале(0 - 

mz),

 то есть 0 < 

и < mz.

Значения потока излучения абсолютно черного тела при раз­

ных температурах приведены в табл. 6.4.

161

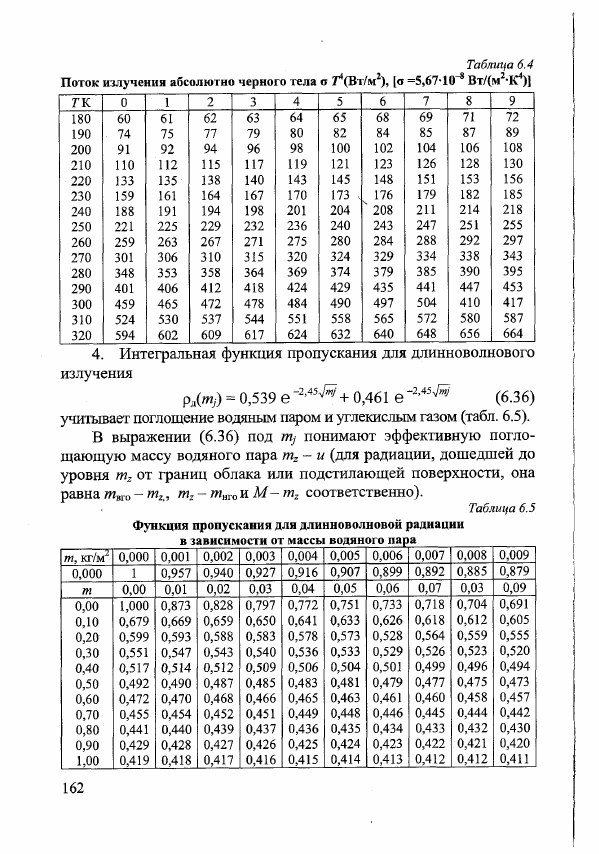
Таблица 6.4

Поток излучения абсолютно черного тела о ГУВт/м2), [о =5,67-1(Г8 Вт/(м2-К4)]

ГК

0

1

2

3

4

5

6

7

8

9

180

60

61

62

63

64

65

68

69

71

72

190

74

75

77

79

80

82

84

85

87

89

200

91

92

94

96

98

100

102

104

106

108

210

110

112

115

117

119

121

123

126

128

130

220

133

135

138

140

143

145

148

151

153

156

230

159

161

164

167

170

173  ,

176

179

182

185

240

188

191

194

198

201

204 '   208

211

214

218

250

221

225

229

232

236

240

243

247

251

255

260

259

263

267

271

275

280

284

288

292

297

270

301

306

310

315

320

324

329

334

338

343

280

348

353

358

364

369

374

379

385

390

395

290

401

406

412

418

424

429

435

441

447

453

300

459

465

472

478

484

490

497

504

410

417

310

524

530

537

544

551

558

565

572

580

587

320

594

602

609

617

624

632

640

648

656

664

4.  Интегральная функция пропускания для длинноволнового

излучения

рд

(mj)

 = 0,539 

е 

-2'45^ +

 0,461 

е ~2,45^  

(6.36)

учитывает поглощение водяным паром и углекислым газом (табл. 6.5).

В  выражении  (6.36)  под  т,  понимают  эффективную  погло­

щающую массу водяного пара 

mz - u

 (для радиации, дошедшей до 

уровня 

mz

 от границ облака или подстилающей поверхности,  она 

равна 

т

вг0

 - 

mZi,  mz

 - 

тшо

 иМ- 

т

2

 соответственно).

Таблица 6.5

Функция пропускания для длинноволновой радиации 

___________________ в зависимости от массы водяного пара_____ ______________

т, кг/м2 0,000 0,001

0,002 0,003 0,004 0,005 0,006 0,007 0,008 0,009

0,000

1

0,957 0,940 0,927 0,916 0,907 0,899 0,892 0,885 0,879

т

0,00

0,01

0,02

0,03

0,04

0,05

0,06

0,07

0,03

0,09

0,00

1,000 0,873 0,828 0,797 0,772 0,751 0,733 0,718 0,704 0,691

0,10

0,679 0,669 0,659 0,650 0,641 0,633 0,626 0,618 0,612 0,605

0,20

0,599 0,593 0,588 0,583 0,578 0,573 0,528 0,564 0,559 0,555

0,30

0,551 0,547 0,543 0,540 0,536 0,533 0,529 0,526 0,523 0,520

0,40

0,517 0,514 0,512 0,509 0,506 0,504 0,501

0,499 0,496 0,494

0,50

0,492 0,490 0,487 0,485 0,483 0,481 0,479 0,477 0,475 0,473

0,60

0,472 0,470 0,468 0,466 0,465 0,463 0,461 0,460 0,458 0,457

0,70

0,455 0,454 0,452 0,451 0,449 0,448 0,446 0,445 0,444 0,442

0,80

0,441 0,440 0,439 0,437 0,436 0,435 0,434 0,433 0,432 0,430

0,90

0,429 0,428 0,427 0,426 0,425 0,424 0,423 0,422 0,421 0,420

1,00

0,419 0,418 0,417 0,416 0,415 0,414 0,413 0,412 0,412 0,411

162

т

0,0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

0,419 0,410 0,402 0,395 0,388 0,382 0,376 0,371

0,366 0,362

2,0

0,358 0,354 0,350 0,347 0,343 0,340 0,337 0,334 0,332 0,329

3,0

0,326 0,324 0,322 0,319 0,317 0,315 0,313 0,311 0,309 0,307

4,0

0,305 0,303

0,301

0,300 0,298 0,296 0,295 0,293 0,292 0,290

5,0

0,288

0,287 0,286 0,284 0,283 0,281

0,280 0,279 0,277 0,276

6,0

0,275 0,274 0,272 0,271

0,270 0,269 0,268

0,266 0,265 0,264

7,0

0,263

0,262 0,261

0,260 0,259 0,258 0,257 0,256 0,255 0,254

8,0

0,253

0,252 0,251

0,250 0,249 0,248 0,247 0,246 0,245 0,244

9,0

0,244 0,243

0,242 0,241

0,240 0,239 0,238 0,238 0,237 0,236

10,0

0,235 0,234 0,234 0,233

0,232 0,231

0,230 0,230 0,229 0,228

т

0

1

2

3

4

5

6

7

8

9

10

0,235 0,228 0,220 0,214 0,208 0,202 0,197 0,191 0,187 0,182

20

0,178 0,174 0,170 0,166 0,162 0,159 0,155 0,152 0,149 0,146

30

0,143

0,141

0,138 0,134 0,133 0,131

0,128 0,126 0,124 0,122

40

0,120 0,118 0,116 0,114 0,112 0,110 0,109 0,107 0,105 0,104

50

0,1021 0,1006 0,0991 0,0977 0,0963 0,0949 0,0935 0,0922 3,0909 0,0897

60

0,0884 0,0872 0,0861 0,0849 0,0838 0,0827 0,0816 0,0805 0,0795 0,0785

70

0,0775 0,0765 0,0756 0,0746 0,0737 0,0728 0,0719 0,0710 0,0702 0,0693

5. 

Интегралы  вычисляются  любым  стандартным  методом 

численного интегрирования, например методом трапеций. В этом 

случае формула (6.26) принимает вид:

т , = т

/ 

\

С 

Л"

§к-\

Рк

- 1

+ §к

р к-\

^ 

Рс

Т 

/

1 Лт J  _

Ь>*-Рг-1|) 

(6-37)

где 

к =

 0,  1,2, ..., 1 - номера уровней, на которых заданы значения

ч(р)-

Интегралы в формулах (6.32)-(6.35) заменяются суммами 

”г 

1 

1

Jo T 4

ф л{ а - т 2) = -  

+ (jIt )\ Рл (K - i 

(K - i 

~т \)

М 

k=i+\

(6.38)

6. 

Потоки  длинноволнового  излучения  можно  определить 

графическим путем, использовав специальную радиационную диа­

грамму (рис. 47).

По осям диаграммы (рис. 48) отложены значения о 

I

4

 и 

pa(mj) 

и нанесены соответствующие им значения аргументов: температу­

ры 

t

 и  поглощающей  массы 

rnj.

  Площадь  элементарной  полоски 

abed

 соответствует произведению ст-74 

-dp^mj).

163

t t   30 

20 

10

-Ю  -20  -30  -50  -70  -90  -120

0,01

0,001

0,1

1

--- 

. _ _  .--- —

 — - „„ ■

 „ - . J00

а

1,4бг/м3  10,002 кзд/{мин-оЛ] 

m  кг/м’

Для решения практических задач масштаб увеличить * 2 раза.

Рис. 47. Радиационная диаграмма

Рис. 48. Схема графического вычисления потоков длинноволновой радиации

164

В 

безоблачной  атмосфере 

восходящий  поток длинноволно­

вой радиации на уровне 

mz

 пропорционален площади 

ABCDF,

 при­

чем площадь 

A B E F

 представляет собой излучение 

земной 

поверх­

ности, а площадь 

B CD E

 - собственное излучение 

атмосферы, 

до­

шедшее до уровня 

mz

 (встречное излучение). Отрезок 

A F

 = а 7^; 

отрезок 

D E

 = р

Д( М -  mzf .

 Нисходящий поток на уровне 

т

2

 пропор­

ционален площади 

CDHG

 i.

Для 

пасмурного  неба, 

если ниже уровня 

mz

 расположено об­

лако так, что его верхняя граница на уровне 

тВТ0,

 то восходящий 

поток пропорционален площади 

A\B\CDEF

 (площадь 

A\B\E\F

 ин­

терпретирует излучение облака), а нисходящий поток определяет­

ся так же, как и при ясном небе.

Если облако расположено выше уровня расчета 

mz,

  восходя­

щий поток имеет такую же величину, как и в случае безоблачной 

атмосферы, а нисходящий поток пропорционален площади 

CD FG

2 

(причем площадь 

CDHiGi

 эквивалентна собственному излучению 

слоя  атмосферы  от  уровня 

mz

  до  нижней  границы  облака 

тш0, 

а площадь 

Y\HiFY

2

 -

 излучению облака, дошедшему до уровня 

mz). 

При  практическом  использовании  масштаб  радиационной  диа­
граммы (рис. 47) рекомендуется увеличить в два раза.

III. Эффективное излучение и радиационный баланс

1. 

Излучение земной поверхности либо измеряется непосредст­

венно, либо вычисляется по формуле:

^ Т ( О )   =   s o I 4 n ,  

( 6 . 3 9 )

где а - постоянная Стефана-Больцмана; 

Тп

 - температура подсти­

лающей земной поверхности; е - коэффициент теплового излуче­

ния (табл. 6.6).

Таблица 6.6

Значения коэффициента теплового излучения 

для некоторых видов земной поверхности______________ __

Вид земной 

поверхности

Коэффициент е

Вид земной 

поверхности

Коэффициент 8

Песок сухой

0,949

Торф сырой

0,983

Песок влажный

0,962

Трава густая

0,986

Почва сухая

0,954

Трава редкая

0,975

Почва влажная

0,968

Снег чистый

0,986

Торф сухой

0,970

Вода

0,960

165