ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 24.04.2019
Просмотров: 359
Скачиваний: 7
1 Что такое случайный процесс?
Случайный процесс – физ. процесс, который описывается случайной функцией (функция
которая в результате опыта принимает тот или иной вид, заранее неизвестно какой именно).
2 Что такое корреляционная функция? Что показывает корреляционная функция
случайного процесса? Что такое интервал (временной) корреляции?
Корреляционная функция – неслучайная функция времени, значения которой в любой
момент равны математическому ожиданию от произведения возможных значений в два
произвольных момента времени. Показывает динамику случайного процесса по времени
(как быстро меняется процесс по времени).
Интервал (временной) корреляции – численная характеристика интервала времени
корреляционной функции, в пределах которого имеет место заметная корреляция между
значениями случайного процесса.
3 Что такое стационарный/нестационарный случайный процесс. Пояснить
графически (на рисунке привести примеры реализаций стационарного и
нестационарного процессов).
Случайный процесс стационарный, если его плотность распределения W
x
(x1, …, xn, t1,…,
tn) не зависит от сдвига во времени.
В противном случае, он называется нестационарным.
(надо ли приводить определение в узком и широком смысле?)
Стационарный:
Нестационарный:
4 В чем состоит эргодическое свойство случайного процесса? Приведите пример
неэргодического случайного процесса.
Эргодическое свойство случайного процесса заключается в том, что статистические
характеристики, полученные по совокупности реализаций, равны статистическим
характеристикам полученных для 1 реализации, но усреднены по времени.
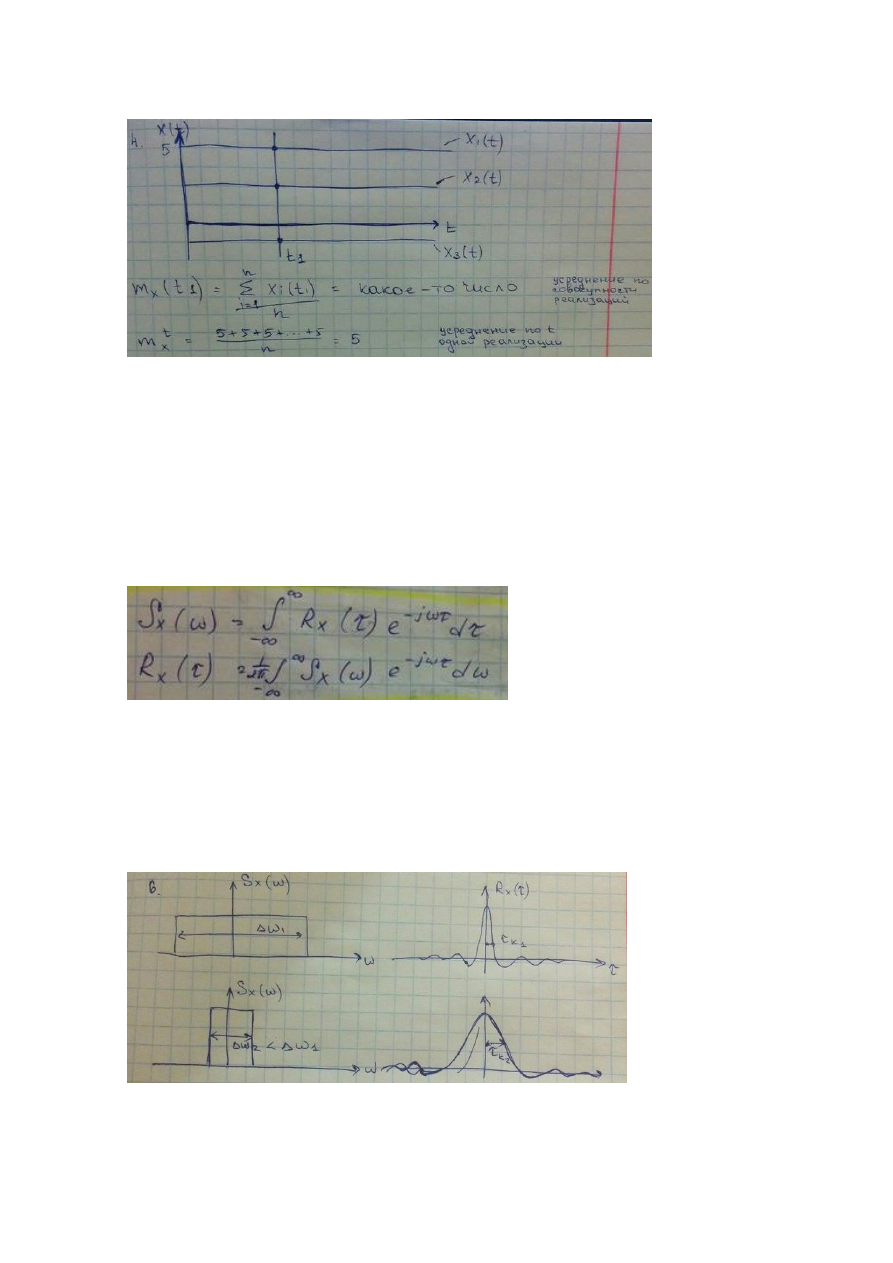
Неэргодический случайный процесс:
5 Что такое спектральная плотность мощности случайного процесса? Как связана
спектральная плотность мощности и корреляционная функция случайного процесса?
Спектральная плотность мощности случайного процесса – это распределение мощности по
полосе частот. Связаны теоремой Винера – Хинчина.
Теорема:
6 Если ширина спектральной плотности мощности уменьшается, то интервал
временной корреляции уменьшается или увеличивается? Пояснить рисунком.
-Увеличивается.
7 Приведите формулировку теоремы Винера-Хинчина? Для чего необходима теорема?
Теорема утверждает о том, что спектральная плотность стационарного случайного процесса
связана с его корреляционной функцией преобразованием Фурье.
8 Что такое белый шум? Какова спектральная плотность мощности и
корреляционная функция спектральной плотности мощности? Как вычисляется
мощность случайного процесса? Чему равна мощность белого шума? Как зависит
мощность ограниченного по полосе шума от полосы?
Белый шум — это стационарный случайный процесс, имеющий постоянную спектральную
плотности мощности для любых частот.
Спектральная плотность мощности белого шума равна константе N
0
=4kT.
Корреляционная функция:
????
????
(????) = ????
0
????(????) – модель белого шума.
Мощность случайного процесса:
????
ш
= ????
ш
=
1
2????
∫ ????
????
(????)????????
∞
−∞
Мощность белого шума равна бесконечности.
Зависимости мощности ограниченного по полосе шума от полосы: P=2N
0
f
гр
.
9 Что такое узкополосный случайный процесс? Что такое широкополосный
случайный процесс? (на рисунке привести примеры реализаций). Имеет ли
широкополосный процесс огибающую?
К узкополосным случайным процессам относят процессы, спектральная плотность
мощности которых сосредоточена в относительно узкой полосе частот в окрестности
некоторой достаточно высокой частоты, т.е. Δf<<f
0
. Особенности УСП является медленное
изменение и случайное во времени огибающая A(t) по сравнению с cos(w0t). Рис. а.
Случайный процесс может быть назван широкополосным, если эффективная полоса частот
его спектральной плотности мощности сравнима со средней частотой этой полосы, либо эта
полоса значительно шире полосы пропускания цепи, через которую проходит данный
сигнал. Рис. б.
Широкополосный процесс также имеет огибающую, только из него косинусоиду трудно
определить в сравнении с УСП
10. Что такое квадратурные составляющие узкополосного случайного процесса и как
они связаны с огибающей и фазой случайного процесса?
X(t) = V(t)cos[ω0t +
(t)] – это случайный процесс
Используя формулу для косинуса суммы двух углов, получим:
X(t) = V(t)cos(
(t))cos(ω0t) - V(t)sin(
(t))sin(ω0t)
Xc(t) = V(t)cos(
(t)) – косинусная квадратурная составляющая.
Xs(t) = V(t)sin(
(t)) – синусная квадратурная составляющая.
Огибающая узкополосного случайного процесса – случайная функция времени, которая в
любой момент времени равна амплитуде гармонического сигнала.
????(????) =
√????????(????)
2
+ ????????(????)
2
.
Фаза - случайная функция времени, которая в любой момент времени равна фазе
гармонического колебания. φ(t)=arctg(x
s
(t)/x
c
(t)).
Огибающая УГСП распределена по закону Рэлея, а фаза по равномерному закону.
11. Какова плотность распределения огибающей и фазы смеси узкополосного
случайного процесса и гармонического сигнала при малом и большом отношении
сигнал/шум?

12. Как преобразуются статистические характеристики случайного процесса при
нестационарном режиме в результате прохождения через линейную цепь?
13. Как преобразуются статистические характеристики случайного процесса при
стационарном режиме в результате прохождения через линейную цепь?
14. Объясните процедуру имитации случайного процесса с заданной спектральной
плотностью.
Для того, чтобы получить случайный процесс с заданной спектральной плотностью, нужно
пропустить случайный процесс через формирующий фильтр. Процедура создания такого
фильтра заключается в следующем:
1) Заданная спектральная плотность мощности аппроксимируется с заданной точностью.
Функция, с помощью которой производится аппроксимация, должна быть представлена
отношением двух полиномов;
2) Полученная рациональная спектральная плотность мощности факторизуется, т.е.
представляется в виде произведения двух комплексно-сопряженных функций частоты;
3) Берется сомножитель, имеющий нули и полюса в верхней полуплоскости комплексного
переменного jω. Он и будет представлять комплексную частотную характеристику
формирующего фильтра.
S
y
(ω)=N
0*
|H(jω)|
2