ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.04.2019
Просмотров: 2061
Скачиваний: 7
46
отношению к средней точке источника питания, как следует из описания
способа модуляции
Его действующее значение, определенное по гладкой составляющей:
Тогда
максимальное
действующее
значение
линейного
напряжения, создаваемое сдвинутыми на 120° фазными напряжениями
:
Тогда максимальное действующее значение фазного напряжения:
Из формул видно, что максимальное действующее значение фазного
напряжения, измеренного относи тельно нуля нагрузки, соединенной
звездой
определенное по гладкой составляющей, равно
максимальному
действующему
значению
фазного
напряжения,
измеренного относительно средней точки источника питания
.
Следовательно, напряжение, действующее между средней точкой
источника питания и нулем нагрузки, не содержит основной гармоники.
Между ними действуют только высшие гармоники, создаваемые разностью
мгновенных значений этих напряжений.
Для регулирования напряжения на выходе АИН необходимо
регулировать амплитуду управляющего (модулирующего напряжения)
.
Глубина регулирования определяется коэффициентом модуляции
47
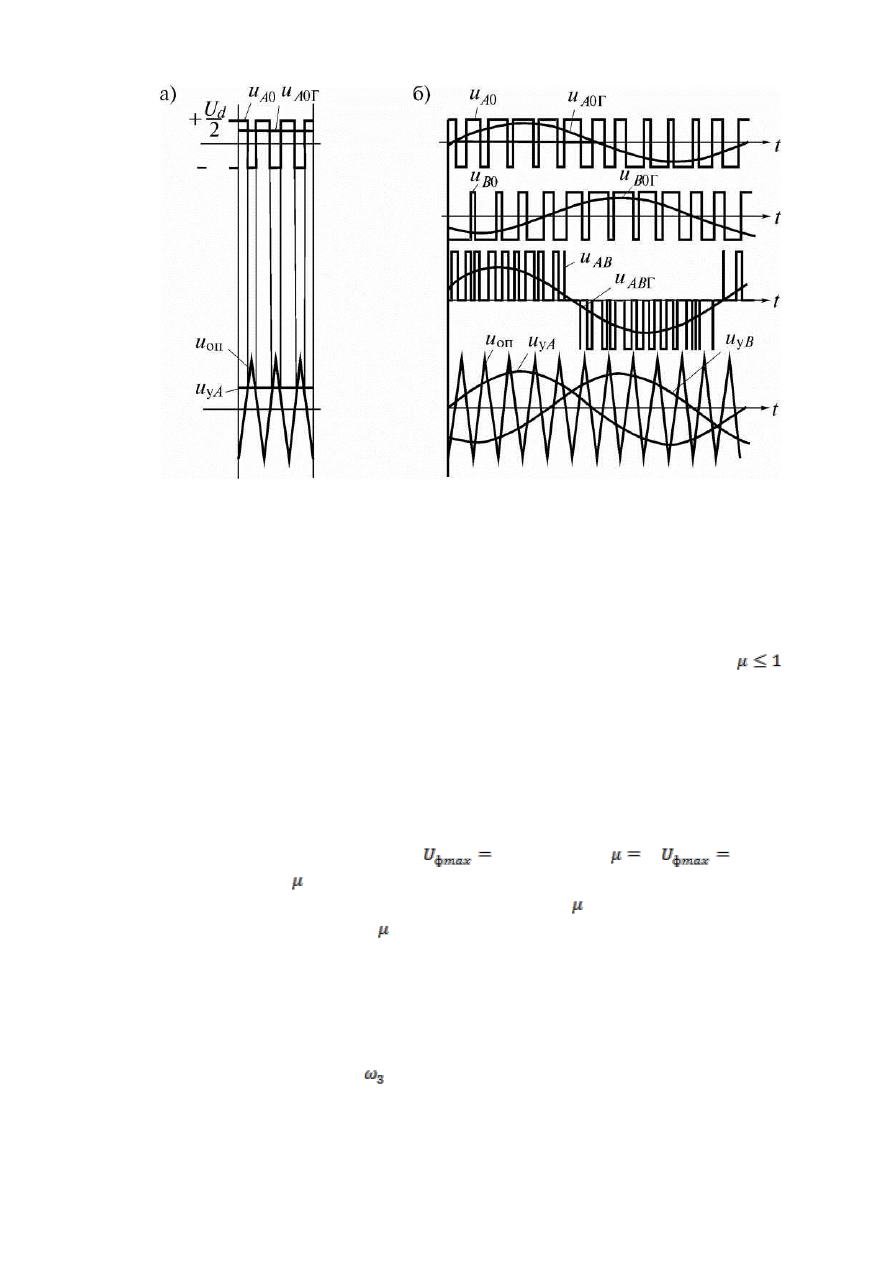
Рисунок 32 – Диаграммы напряжений в трехфазном АИН с
симметричным источником питания при ШИР (а) и ШИМ (б)
Коэффициент модуляции — это отношение амплитуды фазного
напряжения при данном управляющем напряжении к максимальной
амплитуде фазного напряжения. За максимальную амплитуду принята
амплитуда прямоугольного напряжения при отсутствии ШИМ равная Ud/2.
При таком подходе казалось бы всегда должно выполняться условие
.
Однако это не так. Можно и дальше увеличивать амплитуду управляющего
напряжения. При этом модуляция будет прекращаться в центральной части
прямоугольного выходного напряжения, что приводит к появлению
низкочастотных гармоник (пятая, седьмая и т.д.), для борьбы с которыми
требуются фильтры больших габаритов, но одновременно происходит
снижение коммутационных потерь в транзисторах и рост первой
гармоники выходного напряжения. При этом ее максимальное значение в
соответствии с формулой составит
0,45Ud. При
1
35Ud .
Режим, при котором > 1, получил название «сверхмодуляция».
Таким образом, при выполнении условия < 1 осуществляется
синусоидальная ШИМ, а при > 1 ШИМ перестает быть синусоидальной.
Что выбрать, должен решать инженер. Это задача оптимального выбора.
Все приведенные выше максимальные значения соответствуют
только синусоидальной ШИМ.
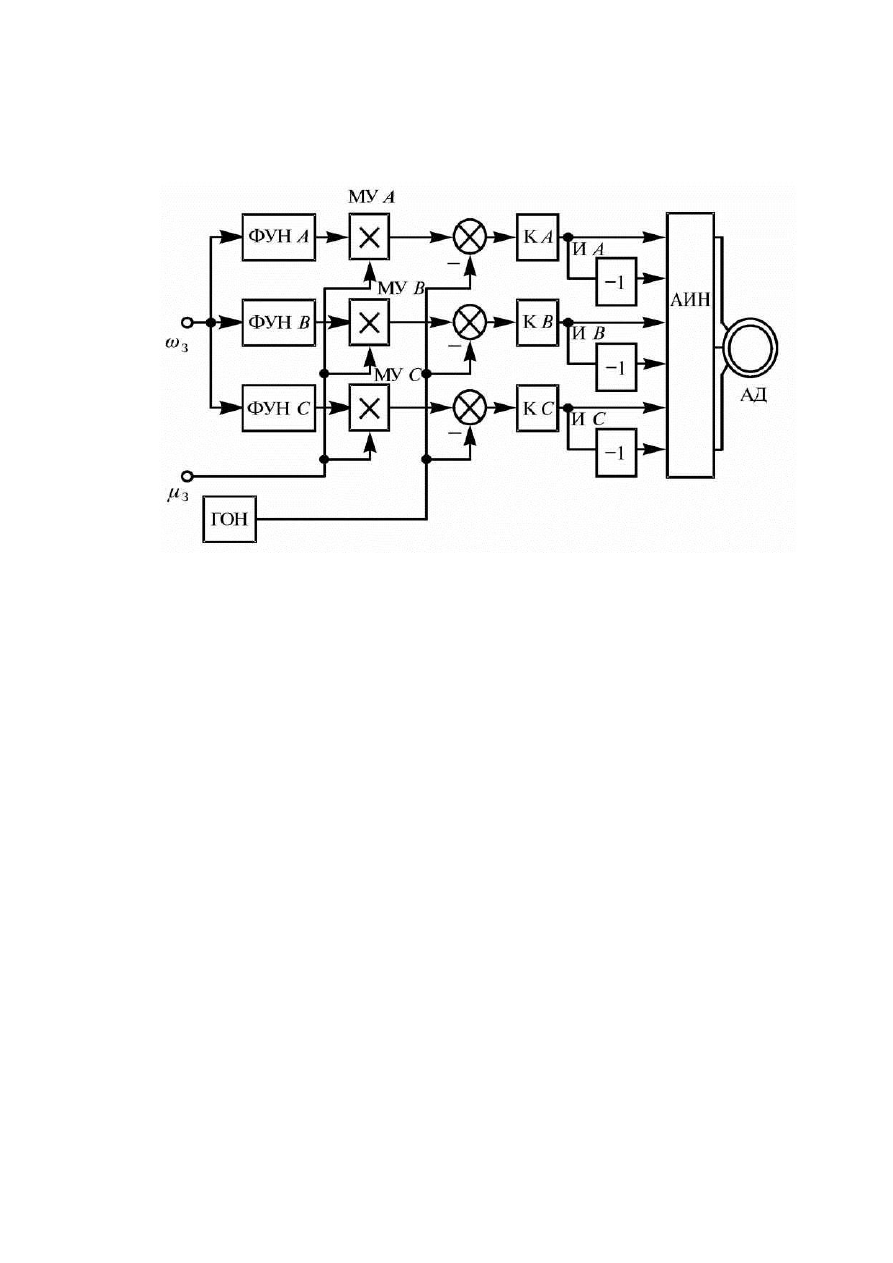
На рис. 33 приведена схема управления, позволяющая реализовать
данный способ управления.
Задание по частоте
подается на вход трех формирователей
максимальных управляющих напряжений фаз ФУН А, ФУН В, ФУН С. В
множительных
устройствах
МУ мгновенные
значения
48
максимальных управляющих напряжений фаз умножаются на заданный
коэффициент модуляции цз и на входах компараторов К сравниваются с
опорным напряжением, подаваемым от генератора опорного напряжения
ГОН.
Рисунок 33 – Функциональная схема системы управления,
формирующей напряжения на выводах по отношению к средней точке
источника питания
Импульсы, сформированные на выходе компараторов, подаются на
усилители мощности (не показанные на рисунке), а с усилителей
мощности на верхние транзисторы (нечетные транзисторы) стоек АИН.
Нижние транзисторы, работающие в противофазе, получают управляющие
импульсы через инверторы И и соответствующие усилители мощности.
Формирование фазных напряжений с помощью пространственного
вектора
Трехфазный АИН с ШИМ должен формировать мгновенные
значения напряжений (средние за период несущей частоты) на трех фазах.
Переключение каждого вентиля изменяет напряжения на всех фазах. Это
осложняет разработку алгоритма управления вентилями. Управление
упрощается, если формировать не фазные напряжения (векторы фазных
напряжений), а перейти к формированию пространственного (не
временного вектора), введенного в теории электрических машин. Согласно
этой теории три симметричных фазных напряжения при отсутствии
нулевого провода могут быть представлены одним пространственным
вектором (space vector), однозначно определяющим эти напряжения. В
литературе этот вектор называют также обобщенным вектором,
результирующим вектором, коммутирующим вектором. Пространственный
вектор U расположен в плоскости перпендикулярной оси вращения
49
ротора.
Вектор, расположенный на плоскости, имеет две координаты. В
полярной системе — это модуль и угол , отсчитываемый против часовой
стрелки от полярной оси до направления вектора. В прямоугольной
системе координат вектор выражается через проекции на вещественную
ось и мнимую ось .
Вещественную ось обычно совмещают с осью фазы «А». Тогда для
фазы «А» угол = 0. Для произвольного угла за период несущей частоты
вектор запишется так
=U
=
.
Если известны мгновенные значения фазных напряжений ,
то
пространственный вектор находится геометрическим суммированием
мгновенных значений, направленных по осям фазных обмоток (сдвинутых
на 120 град.), с последующим умножением на 2/3.
,
где a - оператор поворота на 120 град.
a = -0,5 + j = exp
= 120°.
Проекции вектора на фазные оси дают мгновенные значения фазных
напряжений.
Это справедливо, если в трехфазной системе отсутствует нулевой
провод и обеспечивается равенство нулю суммы мгновенных значений
фазных напряжений
= 0.
Последовательный переход от одного базового вектора к другому
соответствует ступенчатой форме фазных напряжений (см. рис. 34). Для
получения формы фазных напряжений, близкой к синусоидальной, нужно,
чтобы пространственный вектор напряжения двигался, если и не
абсолютно плавно, то хотя бы малыми скачками, занимая положения и
между базовыми векторами. Этого можно добиться, если внутри каждого
периода широтно-импульсной модуляции использовать не один исходный
базовый вектор, а линейную комбинацию исходного и следующего за ним
ненулевого базового вектора, а также один из нулевых векторов. Пусть
требуемый вектор
расположен в секторе 2 (см. рис. 34). Тогда
переключения осуществляются между векторами
,
и нулевым
вектором
, т.е. между замкнутыми состояниями ключей инвертора 1—
2—3, 2—3—4 и 2—4—6 (см. табл. 1)
50
Рисунок 34 – Базовые пространственные вектора
Задача управления инвертором формируется следующим образом:
задано требуемое в данный момент времени положение пространственного
вектора напряжения , т.е. его модель
и угол поворота . Требуется
найти весовые коэффициенты , , определяющие относительные про-
должительности включения комбинации ключей инвертора, соответствую-
щих используемым базовым векторам, т.е. относительные время
включения ключей 1-2-3, 2-3-4 и 2-4-6 соответственно для случая работы
инвертора во втором секторе. Данная задача решена в работе. Для второго
сектора пространственный вектор напряжения может быть описан
следующими уравнениями:
=
+
+
0;
+
=1
Здесь
,
,
- относительные продолжительности включения
комбинации ключей 1-2-3, 2-3-4 и 2-4-6, которые соответствуют базовым
векторам
.
Относительные
продолжительности
,
,
находятся
следующим образом:
=t1/T
шим
;
t2/T
шим
; = t0/T
шим
где t1, t2, t0 - промежутки времени включения этих векторов в
течении времени Tшим.
Уравнение определяют среднее значение пространственного вектора
напряжения как линейную комбинацию составляющих векторов,
выполнение равенства означает, что сумма промежутков времени должна
равняться периоду ШИМ. В дополнение приведенным уравнениям
вводятся ограничения, указывающие на то, что относительные продолжи-
тельности включения не могут быть отрицательными:
0 1; 0 1; 0 1.