ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 01.05.2019
Просмотров: 963
Скачиваний: 1
16
Таблица 2
Уг
ол
з
ап
и
ран
и
я
β
вык
л
ε
β
√
ε
β
√
√
√
√
β
√
ε
β
ε√
ε
√
ε
ε
β
ε
ε
U(
0)
/
U(
0)
/
1
U(
0)
/
U(
0)
/
(U
(0
)+
)/
(U
(0
)-
0,5
Ek0
0
0
0
0
0
+
-0,
5
Uc
(
0)
U
(0
)
U
(0
)
U
(0
)
U
(0
)
U
(0
)
U
(0
)
Сх
ема
Ри
с.
3
.5
с
С
Ри
с.
3
.8
Ри
с.
3
.9
Ри
с.
3
.5
с
L
Ри
с.
3
.6
Ри
с.
3
.7
Ри
с.
3
.1
0
Ри
с.
3
.1
1
Ри
с.
3
.1
2
17
сопротивление контура коммутации:
но
кр
Далее по значению
кр
и выражению для угла запирания β
соответствующего коммутационного узла находят угол β
кр
критического
режима, а по известному времени
выкл
Т
используемых тиристоров с учѐтом
необходимого запаса – угловую частоту:
β
кр
выкл
Т
, где
=1,3…1,5 – коэффициент запаса.
По значениям
и
определяют параметры коммутирующего узла:
;
С
Для иллюстрации методики проведѐм расчѐт элементов узлов
коммутации со следующими данными:
В:
но
А
выкл
Т
мкс В
1. Определяем коэффициент ε
ε
2. Принимаем
СМ
но
3. Коэффициент нагрузки
кр
но
√
ε
СМ
но
√
4. Волновое сопротивление коммутирующего контура
кр
но
5. Угол запирания
18
β
кр
выкл
ε√ε
√ε
ε
√
√
6. Собственная угловая частота контура коммутации
β
кр
выкл
рад/с
7. Ёмкость коммутирующего конденсатора
мкФ
8. Индуктивность коммутирующего дросселя
Гц мГн.
Рисунок 1
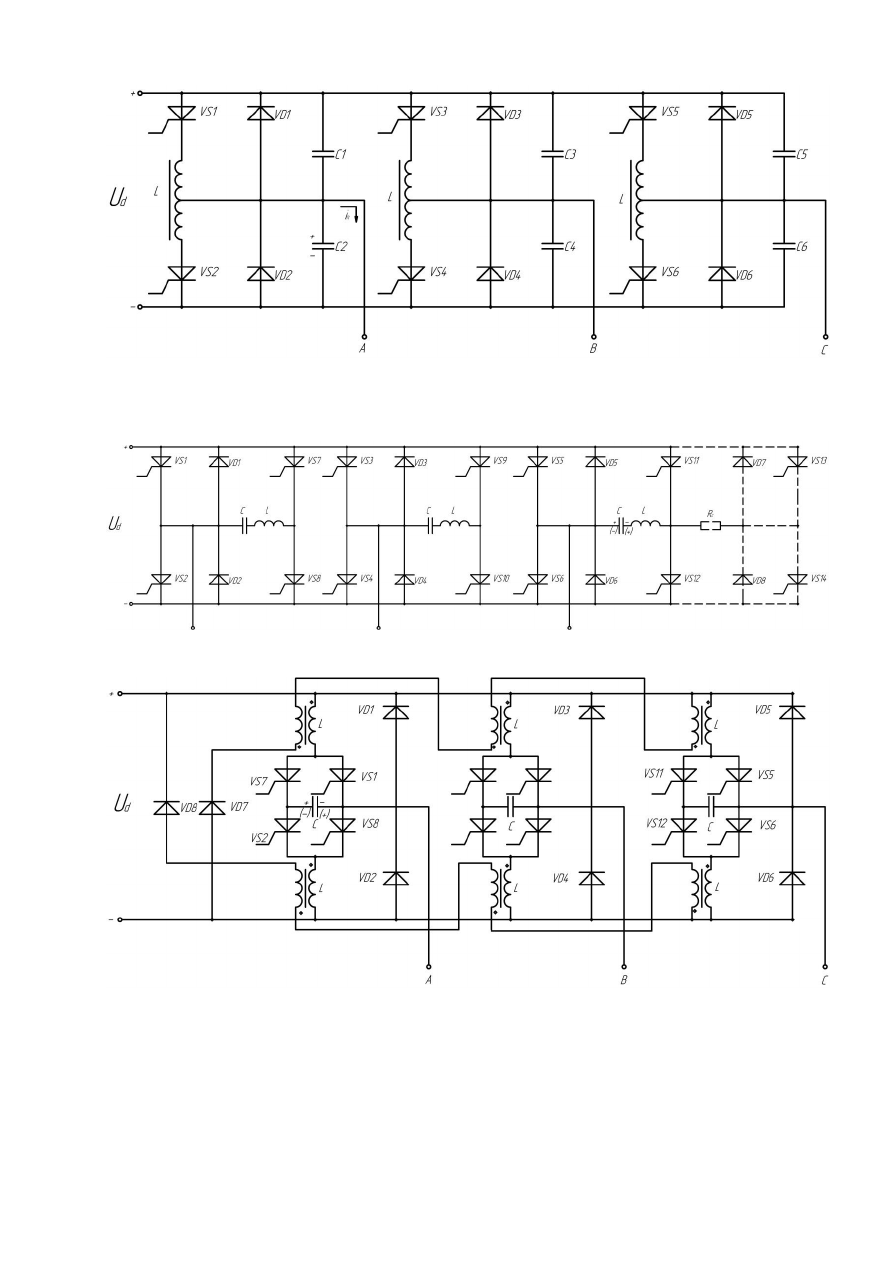
19
Рисунок 2
Рисунок 3
Рисунок 4
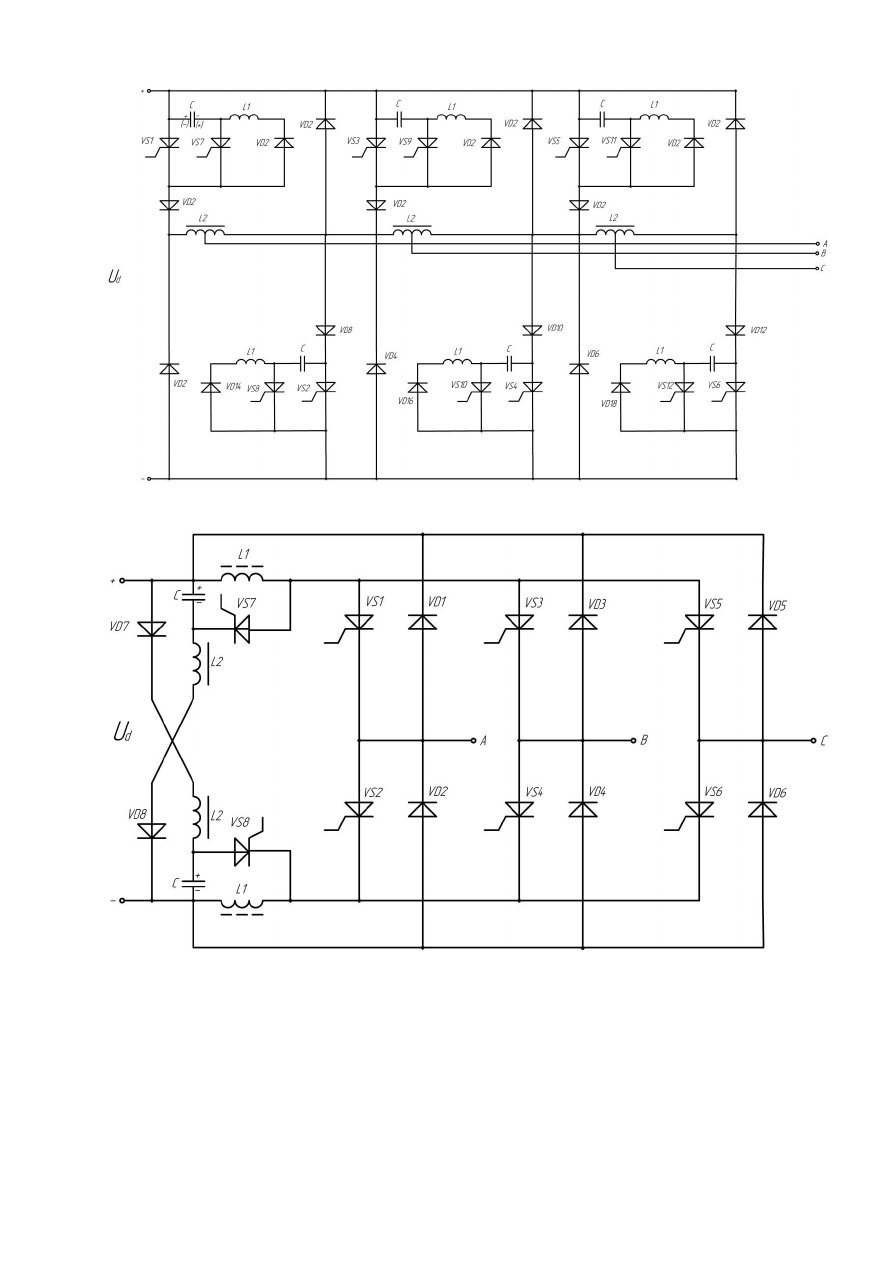
20
Рисунок 5
Рисунок 6