Добавлен: 21.10.2018
Просмотров: 1721
Скачиваний: 17
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Омский государственный технический университет»
И.В. Червенчук, О.П. Шафеева
РЕАЛИЗАЦИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ
Методические указания
О
Составители: И.В. Червенчук, канд. техн. наук, доцент
О.П. Шафеева, канд. техн. наук, доцент
Рассмотрены методы минимизации переключательных функций, разъясняются основные приемы построения комбинационных схем в различных базисах, дается понятие об алгебре высказываний. Приводятся иллюстративные примеры преобразования логических функций и построения комбинационных схем.
Методические указания предназначены для самостоятельной проработки студентами практических заданий по дисциплине «Дискретная математика», содержат материал для подготовки к экзаменам.
Печатается по решению редакционно-издательского совета Омского государственного технического университета
Редактор С.Г. Восканян
ИД № 06039 от 12.10.01
Свод. Темплан 2005 г.
Подписано в печать. Формат 6084 1/16 .Бумага офсетная.
Отпечатано на дупликаторе. Усл. печ. л. 2,0. Уч. изд. л. 2,0
Тираж 200 экз. Заказ
___________________________________________________________________________
Издательство ОмГТУ. 64450, Омск, пр. Мира, 11, тел. 23-02-12.
Т
Практическое занятие 1 МИНИМИЗАЦИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ
ФУНКЦИЙ С ПОМОЩЬЮ КАРТ КАРНО
Цель занятия: изучение способов задания переключательных функций и их минимизация с использованием карт Карно.
Порядок выполнения задания и содержание отчета
-
Построить дизъюнктивную нормальную форму (ДНФ) заданной переключательной функции и представить ПФ картой Карно.
-
Минимизировать ПФ с помощью карты Карно по «единицам» и «нулям». Выбрать минимальное покрытие.
-
Построить минимальные дизъюнктивную (ДНФ) и конъюнктивную (КНФ) нормальные формы ПФ.
Рассмотрим порядок выполнения задания на примерах минимизации ПФ трех, четырех и пяти переменных.
Пример 1
Пусть задана ПФ трех (n=3) переменных в виде совершенной ДНФ (СДНФ)
![]()
![]() (1)
(1)
Карта Карно для
данной ПФ (рис.1) состоит из
![]() клеток. Каждая клетка карты описывается
тремя (n=3)
координатами, причем любые соседние
клетки отличаются одной координатой
[4, 5].
клеток. Каждая клетка карты описывается
тремя (n=3)
координатами, причем любые соседние
клетки отличаются одной координатой
[4, 5].
Д
Рис. 1. Карта
Карно для функции трех переменных
x1
x1
x3
x3
x3
x2
x2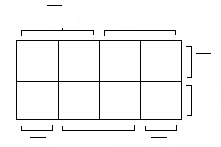
![]() ,
где i,
j
целые числа. Минимальное покрытие единиц
для функции f1
(см. рис.2, а) выделено прямоугольниками,
содержащими
,
где i,
j
целые числа. Минимальное покрытие единиц
для функции f1
(см. рис.2, а) выделено прямоугольниками,
содержащими
![]() и
и
![]() клеток.
клеток.
Каждый прямоугольник
(см. рис.2, а) образует 1-куб, поскольку
объединяет две соседние клетки карты
Карно, отличающиеся по одной координате,
и, следовательно, подвергается операции
склеивания:![]()
![]()
![]() Клетки, лежащие на границах карты
Карно, также является соседними:
Клетки, лежащие на границах карты
Карно, также является соседними:
![]() Одна и та же клетка может покрываться
несколькими различными прямоугольными
(клетка с координатой
Одна и та же клетка может покрываться
несколькими различными прямоугольными
(клетка с координатой
![]() покрывается двумя прямоугольниками
покрывается двумя прямоугольниками
![]() и
и
![]() ).
).
О
Рис. 2. Минимизация
ПФ f1
по «единицам»(а)
и нулям(б) с помощью
карты Карно
x1
x1
x2
x3
x3 a)
б)
x2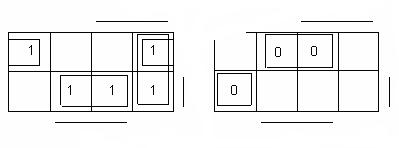

Д![]() изъюнкция
элементарных конъюнкций, описывающих
полученные на карте Карно (рис.2, а)
прямоугольники, образует минимальную
ДНФ функции:
изъюнкция
элементарных конъюнкций, описывающих
полученные на карте Карно (рис.2, а)
прямоугольники, образует минимальную
ДНФ функции:
Для построения ПФ в виде минимальной КНФ целесообразно произвести минимизацию обратного значения ПФ по «нулям». Для этого на карте Карно в клетки с координатами, соответствующими наборам переменных, на которых ПФ принимает нулевые значения, ставиться «0». Далее для нулевых клеток находится минимальное покрытие.
Карта Карно для
обратного значения ПФ
![]() ,
имеет вид (рис. 2, б), ей соответствует
минимальная ДНФ
,
имеет вид (рис. 2, б), ей соответствует
минимальная ДНФ
![]() (2)
(2)
Поскольку цена
покрытия ( количество букв в r-кубах,
покрывающих все «1» или «0» Карно) (![]() ),
представляющего обратное значение ПФ
),
представляющего обратное значение ПФ
![]() меньше цены покрытия ее прямого значения
(
меньше цены покрытия ее прямого значения
(![]() ),
то минимальная ДНФ для обратного значения
ПФ
),
то минимальная ДНФ для обратного значения
ПФ
![]() (2) является более простой.
(2) является более простой.
Используя правила Моргана, из (2) получаем минимальную КНФ ПФ:
![]()
![]()
![]()
Пример 2 Пусть ПФ четырех переменных задана в виде комплекса 0-кубов:
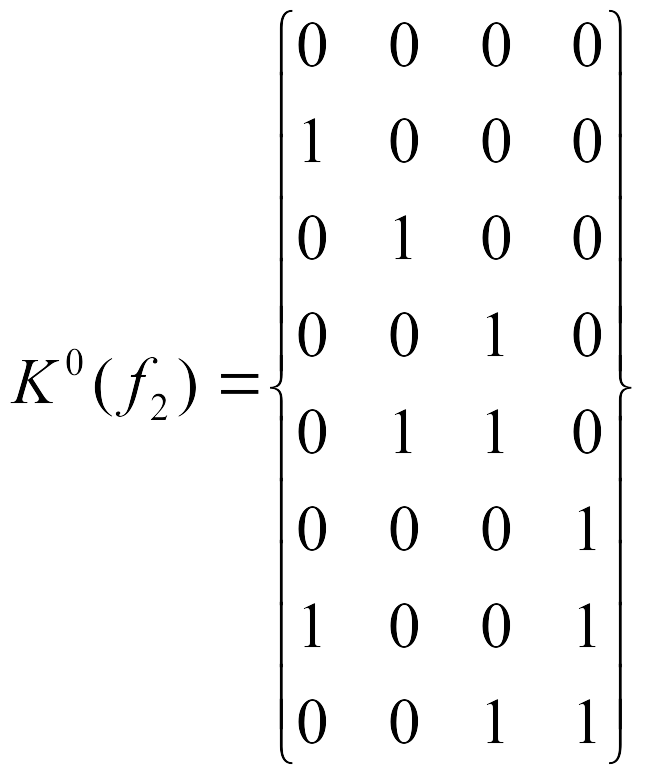
x1
x3
x2
x4 a)
б)
x2
x2
x2
x2
x2
x3
x3
x3
x4
x4

Рис. 3. Минимизация
переключательной функции f2
четырех переменных
Данной ПФ соответствует СДНФ
![]()
![]()
и карта Карно (рис.3, а).
Из рис. 3, а следует, что все единицы заданной ПФ покрываются тремя 2-ку-бами, представляющими прямоугольники из четырех соседних клеток карты Карно. Тогда минимальное покрытие ПФ f2 и минимальная ДНФ примут вид
![]() ,
,
![]() (3)
(3)
Минимизация обратного значения данной ПФ f2 на карте Карно (рис.3, б)
![]() дает КНФ
дает КНФ
![]()
Пример 3
Рассмотрим минимизацию ПФ, заданной с помощью числового представления f3=V(1, 2, 4, 8, 9, 10, 11, 12, 14, 17, 19, 20, 24, 25, 26, 27, 28, 30).
Поскольку номер набора определяет 0-куб и, следовательно, набор переменных, на котором функция равна единице, СДНФ ПФ f3 представляется в виде:
![]()
![]()
![]()
![]() Карта
Карно для ПФ f3
построена на рис. 6, а. Минимальное
покрытие единиц карты определено
прямоугольниками с размерами
Карта
Карно для ПФ f3
построена на рис. 6, а. Минимальное
покрытие единиц карты определено
прямоугольниками с размерами
![]() ,
,
![]() ,
,
![]() ,
объединяющими по 4 и 8 соседних клеток
и образующих 2- и 3-кубы.
,
объединяющими по 4 и 8 соседних клеток
и образующих 2- и 3-кубы.
![]()
x2
x2
x2
x2
x2
x1
x1
x3
x3
x3
x4
x4
x4
x5
x5
x2
x2
x1
x4
x5 a)
б)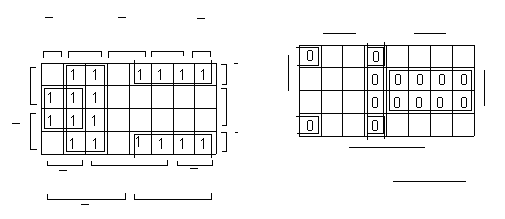
Рис. 4. Определение минимальных ДНФ (а) и КНФ (б) ПФ f3 пяти переменных.
Кубы с наибольшей
размерностью, покрывающие ПФ
![]() (минимизация f3
по «нулям»), приведены на рис.4, б.
Минимальные ДНФ и КНФ представляются
выражениями
(минимизация f3
по «нулям»), приведены на рис.4, б.
Минимальные ДНФ и КНФ представляются
выражениями
![]()
![]()
Пример 4
Пусть задана неполностью определенная ПФ четырех переменных картой Карно (рис.5, а), где прочерками отмечены клетки, которым соответствуют наборы переменных, на которых функция не определена или значение булевой функции безразлично.
x1
x2
x3
x4
x2
x1
x3
x4
x1
x2
x3
x4 a)
в)
б)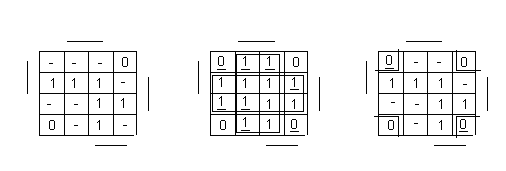
Рис. 5. Минимизация не полностью определенной ПФ
При минимизации не полностью определенных ПФ в клетки карты Карно, заполненные прочерками, записываются нули или единицы таким образом, чтобы получить покрытие «основных» единиц («основных» нулей) наименьшим числом кубов с наибольшей размерностью. Так, для ПФ (рис. 5, а) минимизация по «единицам» (рис.5, б) и по «нулям» (рис. 5, в) дает следующие результаты:
![]()
![]()
Практическое занятие 2 МИНИМИЗАЦИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ МЕТОДОМ КВАЙНА – МАК-КЛАСКИ
Цель занятия: освоить минимизацию переключательных функций методом Квайна–Мак-Класки.
Порядок выполнения задания и содержание отчета
-
Построить дизъюнктивную нормальную форму (ДНФ) заданной переключательной функции и представить ПФ комплексом 0-кубов.
-
Минимизировать ПФ методом Квайна – Мак-Класки. Определить минимальное покрытие.
-
Построить минимальную дизъюнктивную (ДНФ) нормальную форму.
Минимизация переключательной функции методом Квайна – Мак-Класки основывается на использовании правила поглощения, позволяющего вычислить все множество 1-, 2-, … n- кубов, образующих комплекс K(f). Из этого комплекса выделяются кубы наибольшей размерности, покрывающие все множество вершин функции, определяя покрытие Z(f) функции. Покрытие Z(f) упрощается с целью получения минимального.
Как уже отмечалось, 0-куб есть вершина, т.е. булев вектор, или набор аргументов типа «0100», «0000». 1-куб можно рассматривать как вектор, одна координата которого безразлична. Очевидно, что 1-куб может быть образован 0-кубами, различающимися только на одну единицу. Например, «0100» и «0000» образуют
1-куб «0x00». Аналогично 2-кубы образуются из 1-кубов, отличающихся только на 1 единицу (и имеющих «x» в одинаковых позициях), например «0x01» и «0x11» дадут 2-куб «0xx1» и т.д.
В задачах минимизации булевых функций используется понятие простой импликанты. Некоторый куб zK называется простой импликантой, если он не содержится ни в каком другом кубе комплекса К, т.е. не является гранью никакого другого куба из этого комплекса. Совокупность всех таких кубов образует множество Z={z} простых импликант данного комплекса. Любой куб минимального покрытия Сmin является простой импликантой; следовательно, СminZ. Минимизация функции состоит из последовательных этапов.
1. Нахождение простых импликант. Все 0-кубы сравниваются попарно между собой на предмет образования 1-кубов. Если 0-кубы образуют 1-куб, они помечаются. Для упрощения данной операции удобно множество 0-кубов разбить на группы, содержащие равное число единиц, 1-кубы могут быть образованы объединением 0-кубов только из смежных групп. Аналогично производится попытка построить множество 2-кубов на базе множества 1-кубов. Этап заканчивается, когда ни один куб более высокого порядка не может быть построен. Все неотмеченные кубы комплекса K(f) являются простыми импликантами и образуют покрытие Z(f) функции f, которое в общем случае не является минимальным.
2. Составление таблицы покрытий. Задача данного этапа – удалить все лишние простые импликанты. Составляется так называемая таблица покрытий. Строки данной таблицы помечаются простыми импликантами, полученными на шаге 1, столбцы - 0-кубы (термы) минимизированной функции. На пересечении
i-й строки и j-го столбца ставится метка 1, если i-я импликанта покрывает j-й 0-куб, т.е. соответствующие символы совпадают или покрываются символом «x» со стороны импликанты.
3. Определение существенных импликант. Если в каком-либо столбце таблицы покрытий имеется только одна метка, то соответствующая ей импликанта помечается как существенная. Данная импликанта обязательно будет входить в минимальное покрытие, поскольку без нее невозможно покрыть все 0-кубы функции, в определяемое покрытие вносят все существенные импликанты, а из таблицы вычерчиваются соответствующие строки и столбцы, покрываемые данными импликантами.
4. Вычеркивание лишних столбцов. Если в остаточной таблице, полученной после выделения существенных импликант, имеются два столбца, имеющие метки в одинаковых строках, то один из них вычеркивается, т.к. покрытие вычеркнутого столбца обеспечивается за счет покрытия оставшегося столбца.
5. Вычеркивание лишних простых импликант. Если в остаточной таблице имеются строки, не имеющие ни одной метки, импликанты, соответствующие данным строкам, вычеркиваются.
6. Нахождение минимального покрытия. В остаточной таблице, полученной после выделения существенных импликант, выбирается совокупность простых импликант, позволяющих покрыть все столбцы с минимальными затратами. С учетом проведенных вычислений записывается минимальное покрытие как объединение множества существенных импликант и простых импликант, отобранных на данном этапе.
Записывается минимальная ДНФ как дизъюнкция элементов минимального покрытия.
Рассмотрим порядок выполнения задания на примерах минимизации ПФ четырех переменных, минимизация функций с другим числом переменных производится аналогично.
Пример 5
Минимизировать методом Квайна – Мак-Класки ПФ четырех переменных, заданную в виде комплекса 0-кубов:
х1 х2 х3 х4
 1 0 0 0
1
1 0 0 0
1
![]() При записи минимизируемой
функции
При записи минимизируемой
функции
2 0 0
1 0
![]() в виде комплекса К0,
удобно наборы
в виде комплекса К0,
удобно наборы
3 1
0 0 0
![]() разбить на группы (группа
отделена чер-
разбить на группы (группа
отделена чер-
![]()
![]() той), содержащие одинаковое
число
той), содержащие одинаковое
число
5 1 0
0 1
![]() единиц, и пронумеруем
каждый 0-куб.
единиц, и пронумеруем
каждый 0-куб.
6 1
1 0 0
![]() В процессе вычислений
будем также
В процессе вычислений
будем также
7 0 1
1 1
![]() помечать кубы.
помечать кубы.
8 1
1 1 0
![]()
9 1 1
1 1
![]()
Построим комплекс K1, помечая, посредством слияния каких 0-кубов или импликант создана текущая импликанта.
 1 0 0 x
1 1 – 4
1 0 0 x
1 1 – 4
2 x 0 0 1 1 – 5
3 0 0 1 x 2 – 4
4 1 0 0 x 3 – 5
![]() 5
1 x
0 0 3 –
6
5
1 x
0 0 3 –
6
6 0 x 1 1 4 – 7
7 1 1 x 0 6 – 8
8 x 1 1 1 7 – 9
9 1 1 1 x 8 – 9
Построим комплекс
![]() :
:
![]() .
.
Пометим знаком
«![]() »
все импликанты, покрываемые кубами
более высокого порядка.
»
все импликанты, покрываемые кубами
более высокого порядка.
Таким образом, имеем набор простых импликант:
 0 0 x
1
0 0 x
1
x 0 0 1
0 0 1 x
1 0 0 x
![]() 1
x
0 0
1
x
0 0
0 x 1 1
1 1 x 0
x 1 1 1
1 1 1 x
Составляем таблицу покрытий (табл. 1).
Таблица 1
|
Импли-\0-куб канта \ |
0001 |
0010 |
1000 |
0011 |
1001 |
1100 |
0111 |
1110 |
1111 |
|
0 0 х 1 |
1 |
|
|
1 |
|
|
|
|
|
|
x 0 0 1 |
1 |
|
|
|
1 |
|
|
|
|
|
0 0 1 x |
|
1 |
|
1 |
|
|
|
|
|
|
1 0 0 x |
|
|
1 |
|
1 |
|
|
|
|
|
1 x 0 0 |
|
|
1 |
|
|
1 |
|
|
|
|
0 х 1 1 |
|
|
|
1 |
|
|
1 |
|
|
|
1 1 х 0 |
|
|
|
|
|
1 |
|
1 |
|
|
x 1 1 1 |
|
|
|
|
|
|
1 |
|
1 |
|
1 1 1 x |
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|

