Добавлен: 21.10.2018
Просмотров: 1724
Скачиваний: 17
По таблице покрытий находим существенные импликанты, таковая будет только одна (х001), пометим соответствующую единицу вертикально расположенным овалом. Строку, соответствующую существенной импликанте и покрываемые ей столбцы пометим знаком «» и из рассмотрения исключаем.
Далее следует решить задачу о наименьшем покрытии в остаточной таблице, т.е. покрыть минимальным количеством импликант (соответствуют строкам) все истинные наборы (или 0-кубы, соответствуют столбцам). В нашем случае любая импликанты покрывает два набора, обычно при выборе импликант отдается предпочтение тем из них, которые покрывают наибольшее число наборов (их называют короткими импликантами).
Первый столбец (0001) покрывается первой и второй импликантой (00х1 и х001). Здесь, скорее всего, лучше выбрать импликанту х001, поскольку она дополнительно поглощает столбец 1001, тогда как импликанта 00х1 поглощает еще столбец 0011, поглощенный существенной импликантой х001, которая обязательно войдет в решение. Соответствующая единица помечена горизонтально расположенным овалом, строку и столбец, соответствующие выбранной импликанте (х001) и покрываемые ей столбцы пометим знаком «» и из рассмотрения исключаем. Действуя аналогично, рассмотрев столбец 1000 и импликанты 100х и 1х00, выберем импликанту 1х00; рассмотрев столбец 0111 и импликанты 0х11 и х111 выберем импликанту х111, после чего в таблице останется только один не выбранный столбец 1110. Для его поглощения можно выбрать любую из двух импликант: 11х0 или 111х, соответствующие столбцы и строки пометим знаком «».
Таким образом, в данном случае можно построить два минимальных покрытия:
 х
0 0 1 х 0 0 1
х
0 0 1 х 0 0 1
0 0 1 х 0 0 1 х
![]()
![]() 1 х 0 0
1 х 0 0
1 х 0 0
1 х 0 0
х 1 1 1 х 1 1 1
1 1 х 0 1 1 1 х
Запишем результат
в виде ДНФ:
![]() и
и
![]() .
.
Обе минимальные формы равноправны.
Существует формальный алгоритм, называемый алгоритмом Петрика [4, 5], позволяющий автоматизировать решение задачи о наименьшем покрытии остаточной таблицы.
Пример 6
Минимизировать методом Квайна – Мак-Класки ПФ из примера 2.
х1 х2 х3 х4
 1 0
0 0 0
1 0
0 0 0
![]() Запишем минимизируемую функцию
Запишем минимизируемую функцию
2 1 0
0 0
![]() из примера 2, при
этом, для
из примера 2, при
этом, для
3 0 1
0 0
![]() удобства наборы разобьем
на группы,
удобства наборы разобьем
на группы,
![]()
![]() содержащие одинаковое число
единиц, и
содержащие одинаковое число
единиц, и
5 0
0 0 1
![]() пронумеруем каждый 0-куб. В
процессе
пронумеруем каждый 0-куб. В
процессе
6 0 1
1 0
![]() вычислений будем также
помечать
вычислений будем также
помечать
7 1 0
0 1
![]() кубы.
кубы.
8 0
0 1 1
![]()
Построим комплекс K1, помечая, посредством слияния каких 0-кубов или импликант создана текущая импликанта.
1 x
0 0 0 1 – 2
![]()
2 0 x
0 0 1 – 3
![]()
3 0 0 x
0 1 – 4
![]()
4 0
0 0 x
1 – 5
![]()
5 1 0 0 x
2 – 7
![]()
![]() 6
0 1 x
0 3 – 6
6
0 1 x
0 3 – 6
![]()
7 0 x
1 0 4 – 6
![]()
8 0 0 1 x
4 – 8
![]()
9 x
0 0 1 5 – 7
![]()
10 0 0 x
1 5 – 8
![]()
П
 остроим
комплекс
остроим
комплекс
![]() :
:
![]()
![]()
0 0 x х 3 – 10, 4-8
В данном случае
импликанты
![]() покрывают все предыдущие, таким образом,
имеем набор простых импликант:
покрывают все предыдущие, таким образом,
имеем набор простых импликант:
 х 0 0 х
х 0 0 х
![]() 0 х х 0
0 х х 0
0 0 х х .
Составляем таблицу покрытий (табл. 2).
Таблица 2
|
Импли-\0-куб канта \ |
0000 |
1 |
0100 |
0010 |
0001 |
0110 |
1001 |
0011 |
|
х 0 0 х |
1 |
1 |
|
|
1 |
|
1 |
|
|
0 х х 0 |
1 |
|
1 |
1 |
|
1 |
|
|
|
0 0 х х |
1 |
|
|
1 |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
В данной таблице покрытий все импликанты являются существенными (имеют единственную единицу в столбце, соответствующие единицы обведены) . Таким образом, в данном случае имеем минимальное покрытие:
 х
х 0 0
х
х 0 0
![]() 0 х х 0 .
0 х х 0 .
0 0 х х
Запишем результат в виде ДНФ:
![]() .
.
Как видим, результат, полученный методом Квайна – Мак-Класки совпадает с результатом, полученным методом карт Карно.
Практическое занятие 3 СИНТЕЗ КОМБИНАЦИОННЫХ СХЕМ В БАЗИСЕ «И, ИЛИ, НЕ»
Цель занятия: изучение метода синтеза комбинационных схем в логически полном базисе «И, ИЛИ, НЕ».
Порядок выполнения задания и содержание отчета
-
Представить заданную ПФ в виде таблицы истинности, в которой всем возможным наборам аргументов поставлены в соответствие значения функции.
-
Найти минимальную ДНФ (КНФ) ПФ с помощью карты Карно.
-
Составить комбинационную схему ПФ.
-
Проверить комбинационную схему на соответствие заданной ПФ.
Последовательность выполнения задания покажем на примерах.
Пример 7
Пусть задана ПФ
![]() из примера 1 (1). Таблица истинности для
нее имеет вид табл. 3.
Таблица 3
из примера 1 (1). Таблица истинности для
нее имеет вид табл. 3.
Таблица 3
|
Номер набора |
Набор аргументов |
Значение функции |
|
0 1 2 3 4
5
x2 6 7 |
000 00I 0I0 0I I I00 I0I I I0 I I I |
I I 0 I 0 0 I I |
x1
x3
x2
x3
f1
x2
x2
x3
x3
x2
x1
f1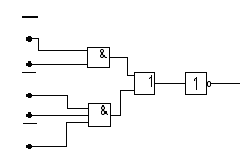
а) б)
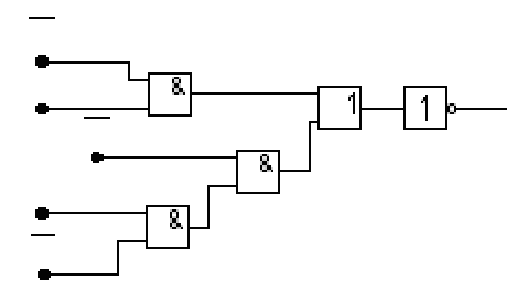
Рис. 6. КС в базисе И, ИЛИ, НЕ
Минимальное представление ПФ (1) найдено в примере 1 и имеет вид (2).
Если набор элементов И, ИЛИ, НЕ для синтеза КС не имеет ограничений по входам, то комбинационная схема функции (2) может быть представлена в следующем виде (рис.6, а).
При использовании лишь двухвходовых элементов операции, реализуемые на одном элементе, группируются в скобки:
![]() (2а)
(2а)
КС для ПФ (2а) (рис. 6, б) может быть реализована по схеме рис. 7.
x3
x1
x2
x2
x3
f1
Рис.7. Комбинационная
схема ПФ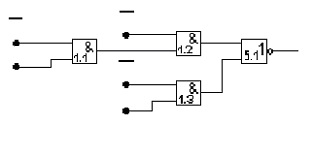
Выполнение проверки правильности работы синтезированной КС (ее соответствие заданной таблицей функции) можно провести «умозрительно», подставляя все возможные входные наборы аргументов или с помощью системы схемотехнического моделирования, например Electronic Workbench. При обнаружении неисправности при контроле КС необходимо проверить правильность заполнения карты Карно, записи z-кубов при минимизации, верность построения схемы.
Пример 8
Для ПФ
![]() =V
(0, 1, 2, 4, 6, 8, 9, 12) таблица истинности
аналогична табл. 1.
=V
(0, 1, 2, 4, 6, 8, 9, 12) таблица истинности
аналогична табл. 1.
Построение КС
двухвходовых элементах (2И, 2ИЛИ) до
минимальной ДНФ данной ПФ (3) возможно
группировкой конъюнкций
![]() При этом потребуется три элемента И и
два элемента ИЛИ.
При этом потребуется три элемента И и
два элемента ИЛИ.
Вынесение же за скобки переменной x1 и получение скобочной формы [4] ПФ
![]()
ведет к упрощению технической реализации, поскольку схема набора в этом случае содержит два элемента И и два элемента ИЛИ (рис. 8).
x1
x2
x3
x4
x5
x4
x2
x1
x3
f2
x2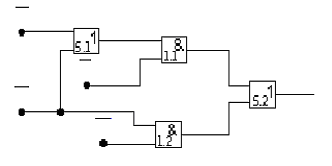

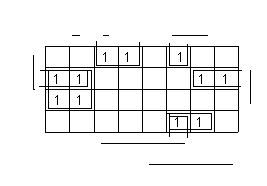
Рис. 8. Комбинационная схема ПФ f2 Рис. 9. Задание ПФ f3 карта Карно
Пример 9
Пусть необходимо синтезировать два варианта КС (на элементах И, ИЛИ без ограничения на число входов и на элементах 2И, 2ИЛИ) для ПФ, заданной картой Карно (рис. 9).
Задать такую ПФ
можно, определив таблицу истинности
или числовое представление ПФ (или КНФ);
![]() ,
поскольку
,
поскольку
ДНФ определят номера наборов, на которых ПФ равна «1» (КНФ задает номера наборов, на которых ПФ принимает значение «0»).
Минимальная ДНФ
ПФ f5,
полученная по карте Карно (рис. 9):
![]()
К
x2
x2
x3
x5
x4
x4
x5
x1
x1
x3
x5
x3
x4
x1
x1
x4
x5
f5
f5
x3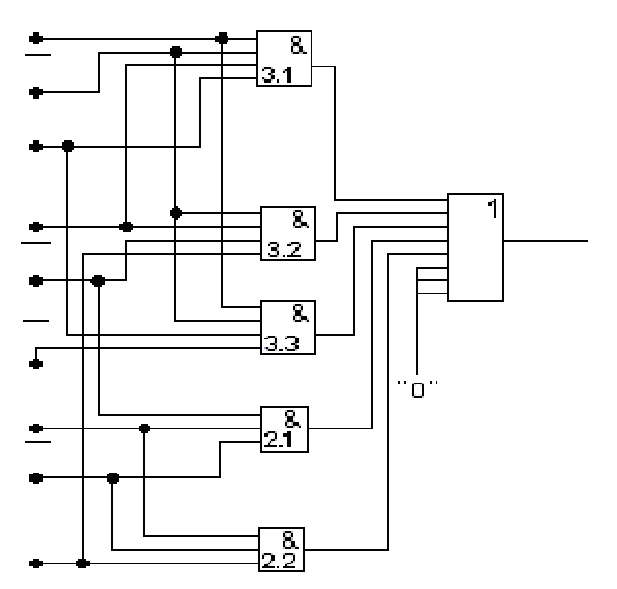
x1
x1
x5
x2
f5
x5
x4
x3
x3
x4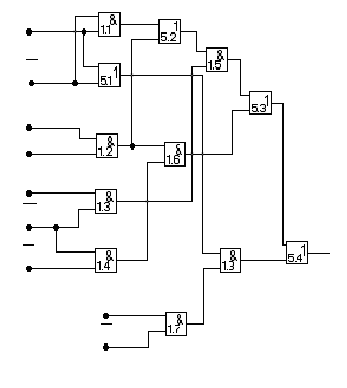
в)
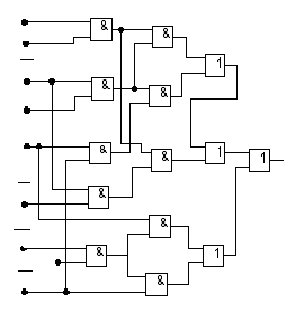
Рис. 10. Схемы реализации ПФ f5 на элементах И, ИЛИ
Упрощение технической реализации КС (рис.10, б) может быть получено помимо вынесения за скобки общих элементов
![]()
выделением одинаковых компонентов (x2х5). В данном случае получается КС, состоящая из 12 элементов с общим числом входов 24 (рис.10, в).
Практическое занятие 4 СИНТЕЗ КОМБИНАЦИОННЫХ СХЕМ
НА ЛОГИЧЕСКИХ ЭЛЕМЕНТАХ И-НЕ
и ИЛИ-НЕ
Цель занятия: изучение правил синтеза КС на универсальных логических элементах И-НЕ, ИЛИ-НЕ.
Порядок выполнения задания и содержание отчета
-
Записать значения заданной ПФ на всех наборах аргументов.
-
Найти минимальную ДНФ (КНФ).
-
Перевести полученную ДНФ (КНФ) для ПФ в базис И-НЕ (ИЛИ-НЕ) без ограничения на число входов и базис 2И-НЕ (2ИЛИ-НЕ).
-
Составить комбинационные схемы ПФ в указанных базисах.
Рассмотрим синтез КС в базисах И-НЕ, ИЛИ-НЕ на примере ПФ
![]() .
.
Минимальное представление ПФ f1 (I) получается минимизацией обратного значения, ДНФ и КНФ для которого имеют соответственно вид:
![]()
![]() .
.
Перевод ПФ в базис И-НЕ производится по представлению минимальной ДНФ
заменой всех дизъюнкций по правилу
![]()
заменой конъюнкций (без инверсий) по правилу
![]()
заменой одной из двойных инверсий по правилу
![]()
![]()
(число сомножителей в правой части выражений зависит от количества входов у используемых элементов И-НЕ), при реализации эта запись означает, что на все входы элемента И-НЕ подается А.
Тогда ПФ f1 в базисе И-НЕ без ограничения на число входов у элементов имеет вид:
![]() .
.
Схема набора данной ПФ на элементах 2И-НЕ и 3И-НЕ показана на рис.11. Сравнение показывает (см. рис. 6, а; 11), что элементы И и ИЛИ заменяются элементами И-НЕ.
x1
x2
x2
x3
f1
x3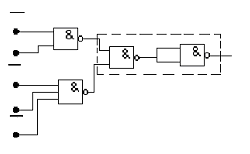
Р
x2
x3
x2
x3
f1
f1
x1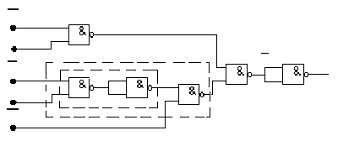
Рис. 12. Схема набора ПФ f1 на элементах 2И-НЕ, 3И-НЕ
Для реализации КС
на элементах 2И-НЕ удобно пользоваться
логической функцией Шеффера
![]() [3]. При этом заданная ПФ переводится в
указанный базис по правилам:
[3]. При этом заданная ПФ переводится в
указанный базис по правилам:
выделяются скобками пары дизъюнкций и конъюнкций (предпочтительным является выделение сочетаний одинаковых букв в разных элементарных конъюнкциях)
![]()
заменяются
пары дизъюнкций конъюнкциями
![]()
![]()
заменяются
пары конъюнкций
![]()
![]()
исключаются
двойные отрицания, поскольку
![]()
![]()
Учитывая, что функция Шеффера реализуется на элементах 2И-НЕ, а отрицание получается подачей на оба входа элемента 2И-НЕ одного и того же (инвертируемого) значения, схема набора функции в базисе 2И-НЕ имеет вид (рис.12). Анализ схем (см. рис.11 и 12) показывает, что элемент 3И-НЕ (см. рис.11) заменяется при переходе к базису 2И-НЕ тремя элементами 2И-НЕ (на рис.11 эта группа элементов выделена), один из которых играет роль инвертора.
Для перехода к базису ИЛИ-НЕ в минимальной КНФ функции производится
замена всех конъюнкций по правилу
,
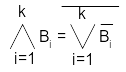
замена всех дизъюнкций (без инверсий)
.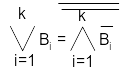
Тогда
![]()
x2
x3
x1
x2
x3
x2
x3
x1
x2
x3
f1
f1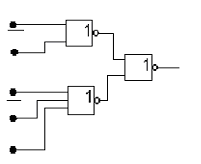
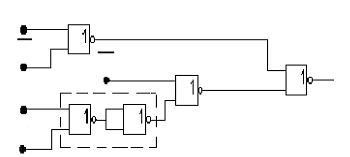
Рис. 13. Комбинационная схема Рис. 14. Комбинационная схема ПФ f1
ПФ f1 на элементах 2ИЛИ-НЕ, на элементах 2ИЛИ-НЕ
3ИЛИ-НЕ
Для перевода ПФ
в базис 2ИЛИ-НЕ рекомендуется пользоваться
логической функцией Пирса
![]() [3] и следующей последовательностью
действий:
[3] и следующей последовательностью
действий:
выделить скобками
пары дизъюнкций и конъюнкций в
представлении ПФ в виде КНФ
![]()
заменить пары
конъюнкций
![]()
![]()
заменить пары
дизъюнкций
![]()
![]()
исключить
двойные отрицания
![]() и заменить одиночные отрицания
и заменить одиночные отрицания
![]()
![]()
Учитывая, что
выражения (![]() )
используются дважды и объединяются
операцией Пирса, выход элемента 2ИЛИ-НЕ,
формирующего (
)
используются дважды и объединяются
операцией Пирса, выход элемента 2ИЛИ-НЕ,
формирующего (![]() ),
подсоединяется к обоим входам следующего
элемента 2ИЛИ-НЕ, что тождественно
получению операции инверсии. Тогда
схема реализации ПФ
),
подсоединяется к обоим входам следующего
элемента 2ИЛИ-НЕ, что тождественно
получению операции инверсии. Тогда
схема реализации ПФ
![]() на элементах 2ИЛИ-НЕ (рис.14)
является четырехуровневой, следовательно,
время формирования входного сигнала
составляет Т=4τ, где τ
время формирования выходного сигнала
одним элементом 2ИЛИ-НЕ.
на элементах 2ИЛИ-НЕ (рис.14)
является четырехуровневой, следовательно,
время формирования входного сигнала
составляет Т=4τ, где τ
время формирования выходного сигнала
одним элементом 2ИЛИ-НЕ.
Практическое занятие 5 СИНТЕЗ КОМБИНАЦИОННЫХ СХЕМ
В СМЕШАННЫХ БАЗИСАХ
Цель занятия: изучение методов синтеза комбинационных схем на логических элементах одной интегральных схем.
Порядок выполнения задания и содержание отчета
-
Записать значения заданной ПФ на всех наборах аргументов.
-
Построить КС для реализации на элементах заданной серии интегральных схем (ИС) с минимальным количеством используемых элементов и (или) минимальным временем формирования выходного сигнала.
-
Проверить правильность работы синтезированной КС.
-
Записать аналитическое выражения для заданной ПФ, позволяющее получить наиболее простую КС на наборе элементов заданной серии ИС.
Рассмотрим пример синтеза КС для функции f1 из примера 1( I ) на двухвходовых логических элементах серии ИС К155 (2И, 2И-НУ, 2ИЛИ, 2ИЛИ-НЕ) [6, 7].
Получение наиболее простой (по количеству элементов) КС при использовании смешанного базиса элементов производится по схемам, построенным в базисах И-НЕ или ИЛИ-НЕ (см. практическое занятие 3). Так, по КС (рис. 14) путем замены пар элементов 2ИЛИ-НЕ и НЕ одним элементом ИЛИ (рис. 15, а) получается схема набора ПФ f1 на элементах 2ИЛИ-НЕ, 2ИЛИ (рис. 16, а), чем достигается упрощение КС до четырех элементов и сокращение времени формирования выходного сигнала до Т= 3τ. Число элементов в КС равно пяти (рис. 6, б, базис 2И, 2ИЛИ, НЕ; Т= 4τ), шести (рис. 12, базис 2И-НЕ; Т=5τ), шести (рис. 14, базис 2ИЛИ-НЕ; Т=4τ).
К подобному упрощению КС рис. 14 до четырех элементов приводит замена элемента 2ИЛИ-НЕ на элемент 2И с инверсией входных переменных (рис. 15, б). КС для ПФ f1 в этом случае реализуется на элементах 2ИЛИ, 2И, 2ИЛИ-НЕ смешанного базиса (рис. 16, б).
fa
fa
fb
fb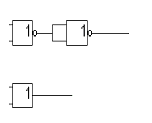
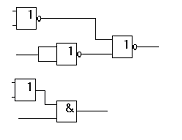
а) б)
Рис.15. Группы элементов, выполняющие равнозначные функции
 000
000