Добавлен: 21.10.2018
Просмотров: 1725
Скачиваний: 17
x3
x2
x3
x2
x1
x1
x2
x3
x3
x2
f1
f1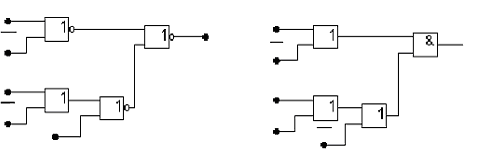
а) б)
Рис. 16. Схема набора ПФ f1 в смешанных базисах
Сравнение всех КС для ПФ f1 на двухвходовых элементах (рис. 6, б, 12, 14, 16) показывает, что реализация данной ПФ получается более простой при использовании смешанного базиса элементов. Кроме того, количество рангов схемы и, следовательно, время формирования выходного сигнала при этом не возрастают.
Практическое занятие 6 СИНТЕЗ КОМБИНАЦИОННЫХ СХЕМ
С ИСПОЛЬЗОВАНИЕМ ДЕШИФРАТОРОВ
И МУЛЬТИПЛЕКСОРОВ
Цель занятия: изучение методов синтеза КС на интегральных схемах средней степени интеграции.
Порядок выполнения задания и содержание отчета
-
Составить функциональную схему заданной ПФ с использованием дешифратора и мультиплексора.
-
Проверить правильность работы синтезированных КС.
В различных сериях интегральных микросхем, выпускаемых в настоящее время, помимо элементов, реализующих простые логические функции И, ИЛИ, НЕ, ИЛИ-НЕ и др., имеются элементы, выходные сигналы которых описываются более сложными логическими функциями. Примерами таких элементов являются дешифраторы и мультиплексоры, реализованные в виде интегральных схем средней степени интеграции. Большие функциональные возможности дешифраторов и мультиплексоров позволяют в ряде случаев существенно упростить процедуру синтеза КС.
В дальнейшем под
дешифратором будем понимать КС, имеющую
n
основных входов и
выходов (при
дешифратор называется полным). Помимо
основных входов у дешифратора могут
быть дополнительные, сигналы на которых
разрешают или запрещают реализацию
выходных функций. Обозначим логические
переменные, подаваемые на основные
входы дешифратора через
а на дополнительные – через
.
Тогда выходные функции дешифратора
могут быть представлены табл. 4.
Таблица 4
|
X…X3X2X1 |
Ck…C2C1 |
Y0Y1Y2…Y2n-1 |
|
0… 0 0 0 |
1… 1 1 |
1 0 0 … 0 |
|
0… 0 0 1 |
1… 1 1 |
0 1 0 … 0 |
|
0… 0 1 0 |
1… 1 1 |
0 0 1 … 0 |
|
…………… |
……….. |
……………….. |
|
1… 1 1 1 |
1… 1 1 |
0 0 0 … 1 |
|
X… X X X |
X… X 0 |
0 0 0 … 0 |
|
X… X X X |
X… 0 X |
0 0 0 … 0 |
|
…………… |
………… |
………………... |
|
X… X X X |
0… X X |
0 0 0 … 0 |
Под X в табл. 4 и последующих таблицах подразумевается произвольное значение логической переменной
Из табл. 4 следует,
что при
на каждом выходе дешифратор реализуется
ПФ, СДНФ которой состоит лишь из одного
произведения переменных, определенного
номером выхода. Так, на выходе
реализуется ПФ
а на выходе
и так далее. Формирование на выходах
дешифратора всевозможных
конъюнкций n
переменных позволяет очень просто
проводить синтез КС. Для этого достаточно
на основные входы дешифратора подать
переменные реализуемой ПФ, на дополнительные
– значения логических единиц, выходы
дешифратора, соответствующие произведениям
переменных, входящих в СДНФ реализуемой
ПФ, соединить со входам элемента ИЛИ,
на выходе которого будут формироваться
значения ПФ.
Таблица 5
-
x3
x2
x1
C1
Y0
Y1
Y2
Y3
Y4
Y5
Y6
Y7
0
0
0
1
1
0
0
0
0
0
0
0
0
0
1
1
0
1
0
0
0
0
0
0
0
1
0
1
0
0
1
0
0
0
0
0
0
1
1
1
0
0
0
1
0
0
0
0
1
0
0
1
0
0
0
0
1
0
0
0
1
0
1
1
0
0
0
0
0
1
0
0
1
1
0
1
0
0
0
0
0
0
1
0
1
1
1
1
0
0
0
0
0
0
0
1
X
X
X
0
0
0
0
0
0
0
0
0
Несколько более
сложную задачу представляет синтез Кс
на дешифраторах, если число переменных
реализуемой ПФ больше, чем число основных
входов дешифратора. В этом случае
требуется более одного дешифратора,
каждый из которых имеет хотя бы
дополнительный (стробирующий) вход.
Пусть, например, требуется провести
синтез КС, реализующей функцию
на дешифраторах с тремя основными
входами и одним стробирующим входом.
Входные функции такого дешифратора
определяются табл. 5, а заданная ПФ –
табл. 6.
Таблица 6
-
Аргументы
функции
x2x1
0 0
0 I
I 0
I I
x4x3
0 0
0
I
I
0
0 I
I
0
0
I
I 0
I
0
0
I
I I
0
I
I
0
СНДФ заданной ПФ
имеет вид:
Преобразуем ее
путем вынесения за скобки переменных
и
:
В полученном
выражении в круглых скобках записаны
СНДФ ПФ, зависящих от трех аргументов,
которые могут быть реализованы с
использованием заданных дешифраторов.
Переменная
должна быть подана на вход
первого дешифратора, а
на вход
второго дешифратора. Это обеспечит
формирование значений заданной ПФ
выходными сигналами первого шифратора
при
или второго при
КС, реализующая функцию
приведена
на рис. 17.
При наличии инверсных выходов у дешифратора в качестве объединительного вместо элемента ИЛИ должен быть использован элемент И-НЕ. Наличие нескольких дополнительных входов C у дешифратора позволяет реализовать логические функции над переменными, подаваемыми на стробирующие входы.
Проиллюстрируем
указанную возможность на примере
использования дешифратора с двумя
стробирующим входами для реализации
ПФ
Преобразуем СДНФ функции к виду
(рис. 18).
x2
x3
x1
x4
x1
x2
x3
x4
f(x1
x4)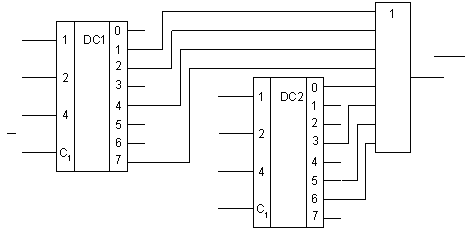
x1 
x2
x3
x4
x1
x2
x3
x4
f(x1
x4)
x1
x2
x3
x4
x1
x2
x3
x4
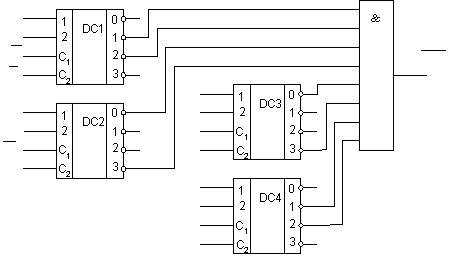
Рис. 18. КС,
реализующая ПФ
использующая
дешифраторы с двумя основными входами
Если число переменных ПФ меньше числа входов дешифратора, то при синтезе КС на свободные входы дешифратора с большими весами должны быть поданы нулевые значения логических переменных.
Рассмотрим теперь
методику синтеза КС на мультиплексорах.
Мультиплексором будем называть КС,
имеющую m
управляющих входов, 2m
информационных входов и один выход.
Выходной сигнал мультиплексора совпадает
с сигналом на i-ом
информационном входе, если на его
управляющие входы подан двоичный код
числа i.
Обозначим управляющие входы мультиплексора
A1,
A2,
…, Am
а информационные –
Тогда выходная функция мультиплексора
может быть представлена как ДНФ ПФ,
зависящей от n=(m+1)
переменных:
Пусть с помощью
мультиплексора требуется провести
синтез КС, реализующей ПФ
.
Подадим переменные
на управляющие входы мультиплексора
тогда выходная функция мультиплексора
примет вид:
Определим значения
переменных, которые необходимо подать
на информацон-ные входы мультиплексора.
Для этого выделим в таблице истинности
ПФ
пары строк, отличающиеся только значением
переменной Х1.
Таких пар будет 2m.
В каждой паре выделенных строк таблицы
истинности сравним значение ПФ
со значениями переменной x1.
Поскольку в одном
из наборов пары x1=0,
а в другом x1=1,
то результатов сравнения может быть
четыре:
Результат сравнения
определяет, что должно быть подано на
информационный вход мультиплексора,
номер которого определяется переменными
рассматриваемой пары.
Реализуем, например, с помощью мультиплексора ПФ, заданную табл. 7. Поскольку ПФ зависит от трех переменных, то для синтеза КС требуется мультиплексор с двумя управляющими входами. В последнем столбце (табл. 7) указан номер информационного входа, подключаемого к выходу мультиплексора, при подаче на его управляющие входы переменных x2 и x3.
Таблица 7
-
x3x2x1
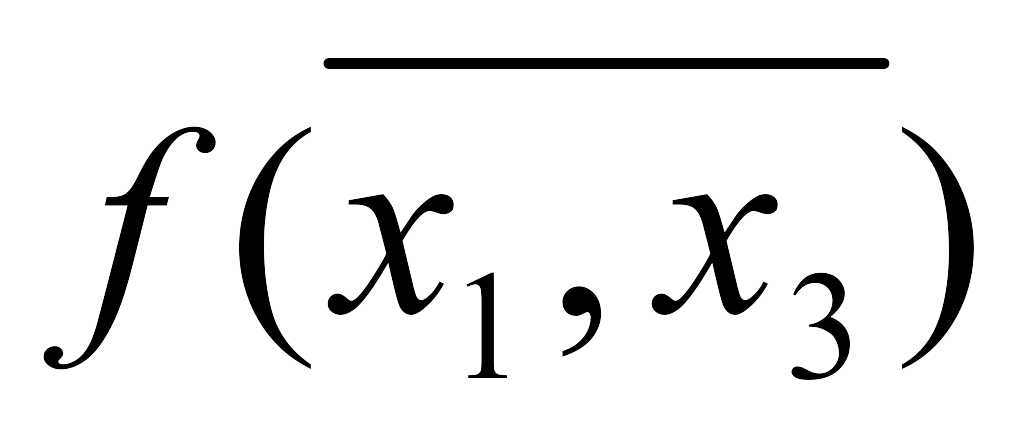
Вход
0 0 0
0 0 I
I
0
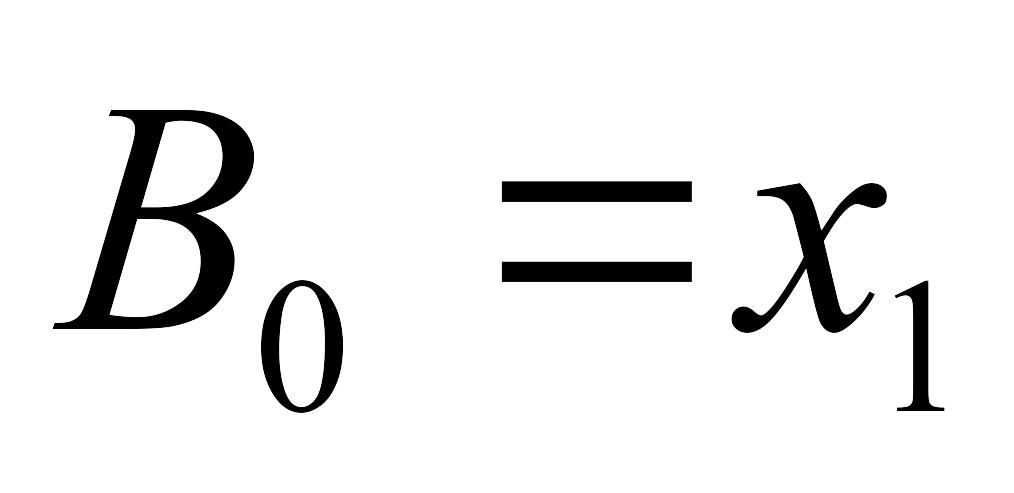
B0
B0
0 I 0
0 I I
I
I
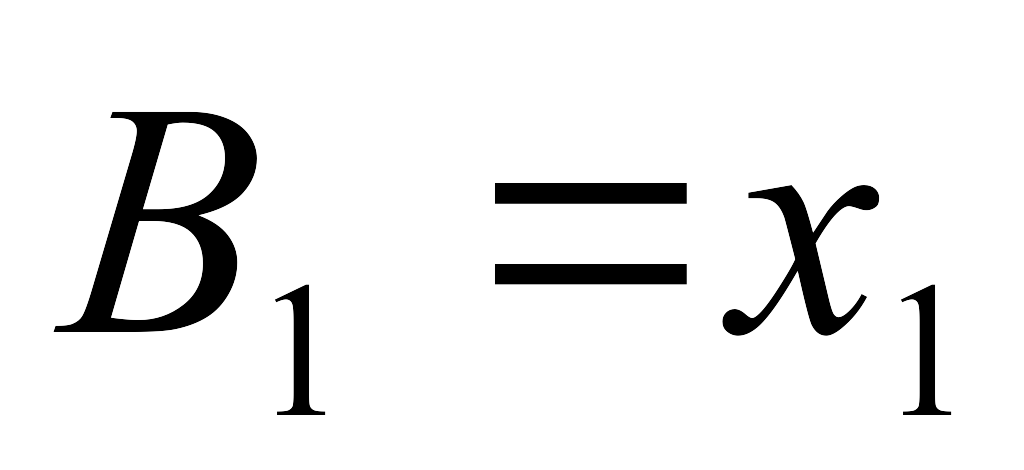
B1
B1
1
I 0 0
I 0 I
0
0
B2
B2
0
I I 0
I I I
0
I
B3
B3
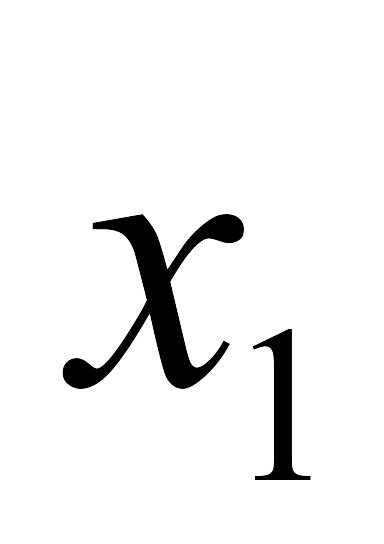
Таблица
8
-
MS1
MS2
x4
0
0
0
0
0
0
0
0
I
I
I
I
I
I
I
I
x3
0
0
0
0
I
I
I
I
0
0
0
0
I
I
I
I
x2
0
0
I
I
0
0
I
I
0
0
I
I
0
0
I
I
x1
0
I
0
I
0
I
0
I
0
I
0
I
0
I
0
I
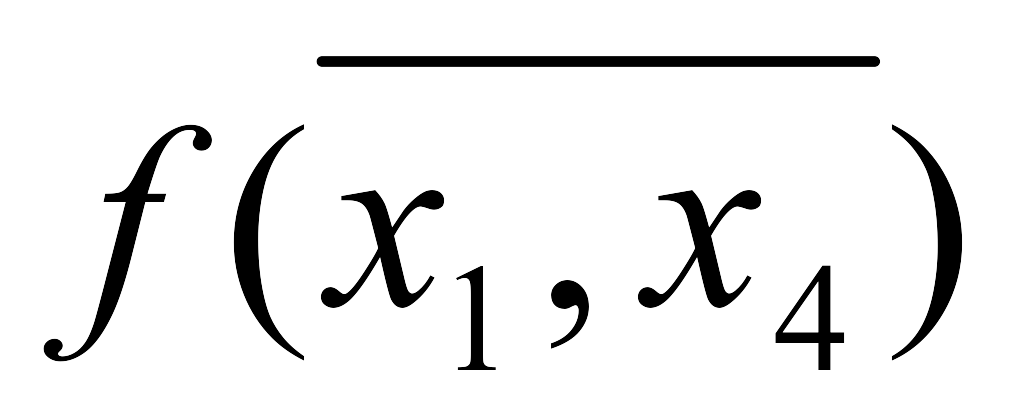
0
I
0
I
0
I
I
I
0
I
I
I
I
I
I
I
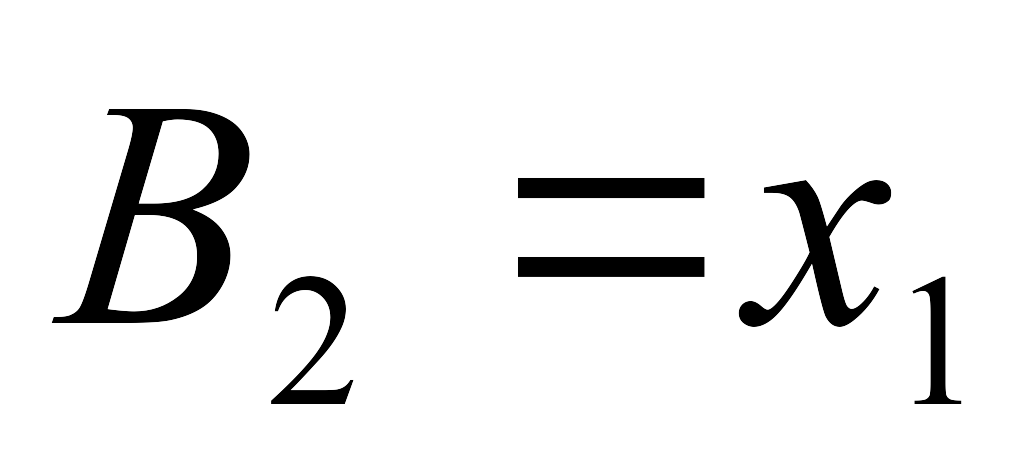
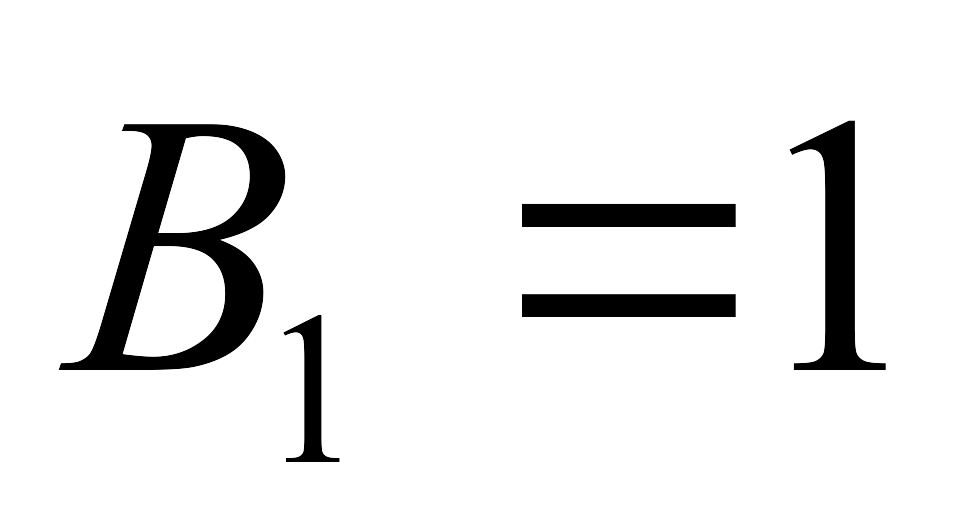
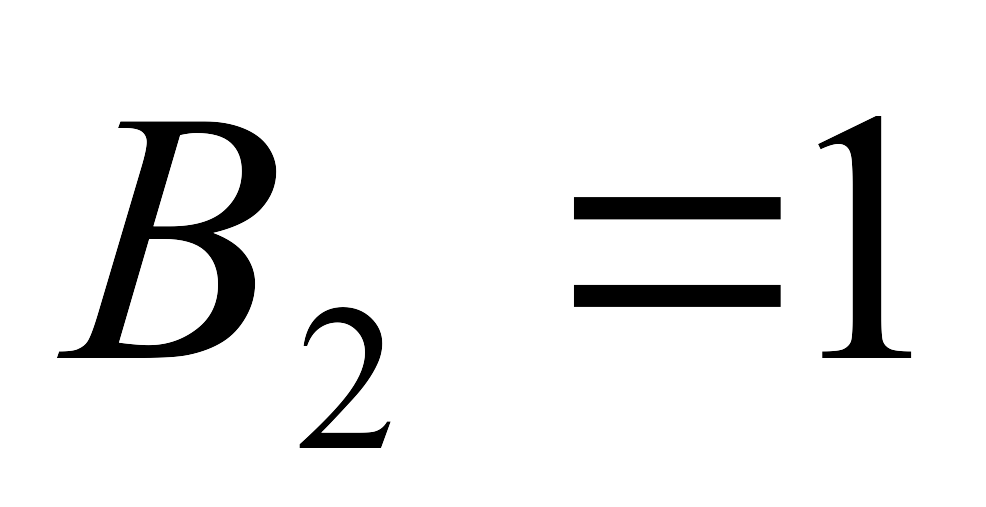
П
x2 
то на информационный вход В0
должна быть подана переменная
На остальные информационные входы (в
порядке возрастания номеров) подаются
постоянная единица, постоянный ноль,
переменная x1,
поскольку
Заданная ПФ реализует с помощью КС
(рис.19).
x1
x3
x1 0 1
f(x1
x3)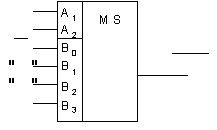
Рис. 19.КС, реализующая ПФ, заданную табл. 7
f(x1
x4)
x3
x2
x1 1
x4
x2
x3
x1
x4 1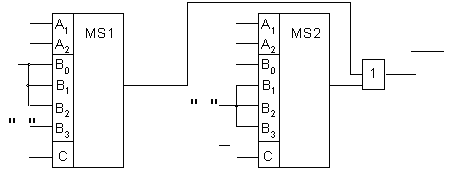
Рис. 20. КС, реализующая ПФ, заданную табл. 8.
При наличии у
мультиплексора стробирующих входов
для реализации ПФ, зависящей от n
переменных, могут быть использованы
мультиплексоры с числом управляющих
входов меньше чем n-1.
Пусть, например, ПФ зависит от четырех
аргументов (табл. 8), а для синтеза КС
используются мультиплексоры с двумя
управляющими входами и одним стробирующим,
нулевой сигнал, на котором разрешает
работу мультиплексора. Тогда, подав на
управляющие входы А1,
А2
обеих мультиплексоров переменные x2,
x3,
на вход С первого мультиплексора
переменную x4,
на вход С второго мультиплексора
переменную
,
а на информационные входы – переменные,
определяемые соотношением значений
и x1
в парах двоичных наборов при фиксированных
значениях x2,
x3,
получим КС, реализующую заданную ПФ
(рис. 20). При x4=0
работает первый мультиплексор, при x4=1
–второй.
Если требуется
обеспечить подачу на большую часть
информационных входов мультиплексора
логических констант «1» и «0», то следует
проанализировать все возможные варианты
подачи на управляющие входы переменных
реализуемой ПФ. Например, при реализации
ПФ
(табл. 8) с помощью мультиплексора с тремя
управляющими входами подача на них
переменных x2,
x3,
x4
ведет к
тому, что переменная x1
будет подана на входы В0,
В1,
В2,
В4.
Если на управляющие входы подать
переменные x1,
x2,
x3,
то переменная x4
будет подана только на информационные
входы В2
и В4.
На остальные информационные входы будут
поданы константы 0 и 1.
Указанную процедуру следует выполнять
в тех случаях, когда необходимо снизить
нагрузку на выход элемента, формирующего
значение логической переменной на
информационных входах мультиплексора.
Практическое занятие 7 АЛГЕБРА ВЫСКАЗЫВАНИЙ
Цель занятия: изучение формализма алгебры высказываний, решение логических задач методами формальной логики.
Язык
алгебры высказываний это по существу
булева алгебра в широком смысле, которую
максимально приблизили к естественному
языку. Носителем этой алгебры являются
высказывания. Причем под высказыванием
здесь понимается любое повествовательное
предложение, о котором можно сказать
истинно оно или ложно. Например, «Волга
впадает в Каспийское море» – истинное
высказывание, а «
»
– ложное.
Сигнатурой
алгебры высказываний является следующее
множество логических операций соединения
.
Эти операции, как уже отмечалось выше,
подобны союзам русского языка и
обеспечивают получение из простых
высказываний сложные.
Тождества данной алгебры определяются тождествами булевой алгебры, к которым добавляются еще три тождества
определение
импликации;
определение
эквиваленции;
определение
сложения по модулю 2.
Определение 1. Высказывание называется атомарным, если оно соответствует простому предложению (т.е. не содержащему в себе соединительных и разделительных союзов и знаков пунктуации) и обозначается некоторым символом как единое и неделимое целое.
Например, высказывание «Алеша, Кирилл, Паша, Володя ученики третьего класса» не является атомарным, поскольку соответствует предложению содержащему запятые, которые в данном случае определяют логическую операцию – конъюнкцию. Данное высказывание есть конъюнкция четырех атомарных высказываний: «Алеша ученик третьего класса», «Кирилл ученик третьего класса» и т.д.
Для обозначения высказываний условимся использовать прописные буквы русского алфавита: А, Б, …, Я. В случае необходимости будем использовать также и индексы.
Неатомарные (сложные) высказывания в алгебре высказываний изображаются в виде булевых формул. Данные формулы должны удовлетворять определенным правилам записи. Введем понятие правильно построенной формулы (ППФ).
Определение
2.
Символ, соответствующий атомарному
высказыванию есть ППФ. Если
и
правильно построенные формулы, то
также ППФ. Правила использования круглых
скобок для установления порядка
выполнения логических операций аналогичны
правилам элементарной алгебры.
Булева алгебра и язык высказываний позволяют довольно успешно решать различные логические задачи. Методика их решения при этом может быть задана следующим алгоритмом.
Алгоритм
Шаг 1. Исследовать текст условия задачи. Выделить в нем атомарные высказывания и ввести для них условные обозначения. Следует стремиться к тому, чтобы число таких атомарных высказываний было наименьшим. Это число определяет размерность гиперкуба, включающего в себя область истинности ППФ, определяющей условие решаемой задачи. Чем меньше это число, тем проще формула, подлежащая упрощению.