Добавлен: 21.10.2018
Просмотров: 2013
Скачиваний: 9
19
2.2 Математическая часть
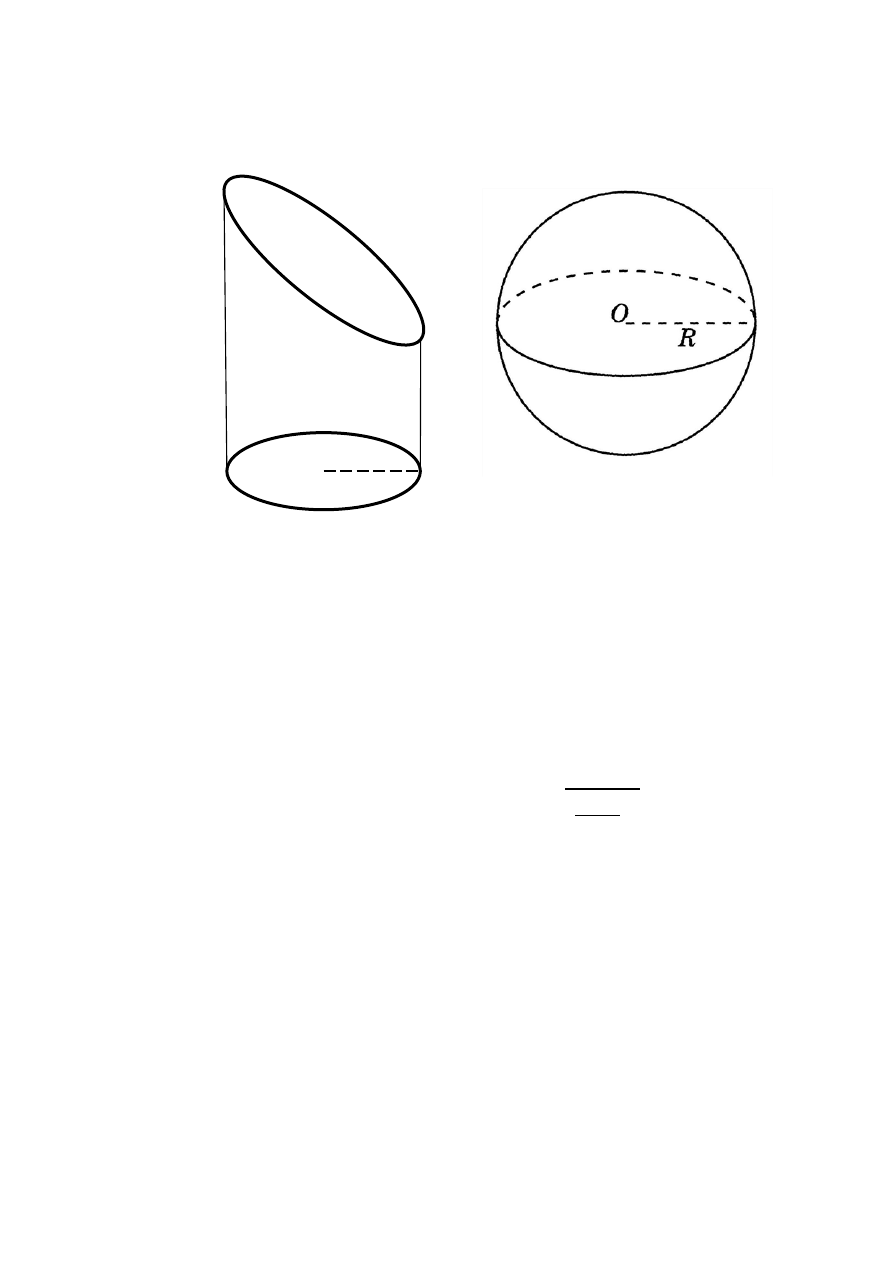
Фигуры, рассматриваемые в задании, приведены на рисунке 1.
a)
b)
Рисунок 1 – Геометрические фигуры
Цилиндр – геометрическое тело, ограниченное цилиндрической
поверхностью и двумя параллельными плоскостями, пересекающими ее.
Площадь поверхности усеченного круглого цилиндра с радиусом
оснований r и высотой h вычисляется по формуле [6]:
????
ц
= ???????? (ℎ
1
+ ℎ
2
+ ???? + √(
ℎ
2
−ℎ
1
2
)
2
),
где h
1
и h
2
– высоты, r – радиус основания.
Шар – геометрическое тело; совокупность всех точек пространства,
находящихся от центра на заданном расстоянии, которое называется радиус.
Площадь поверхности шара вычисляется по формуле [6]:
????
ш
= 4????????
2
,
где R – радиус шара.
Для решения поставленной задачи необходимо выполнение условия:
????
ц
< ????
ш
.
r
h
2
h
1
20
2.3 Описание алгоритма решения задачи
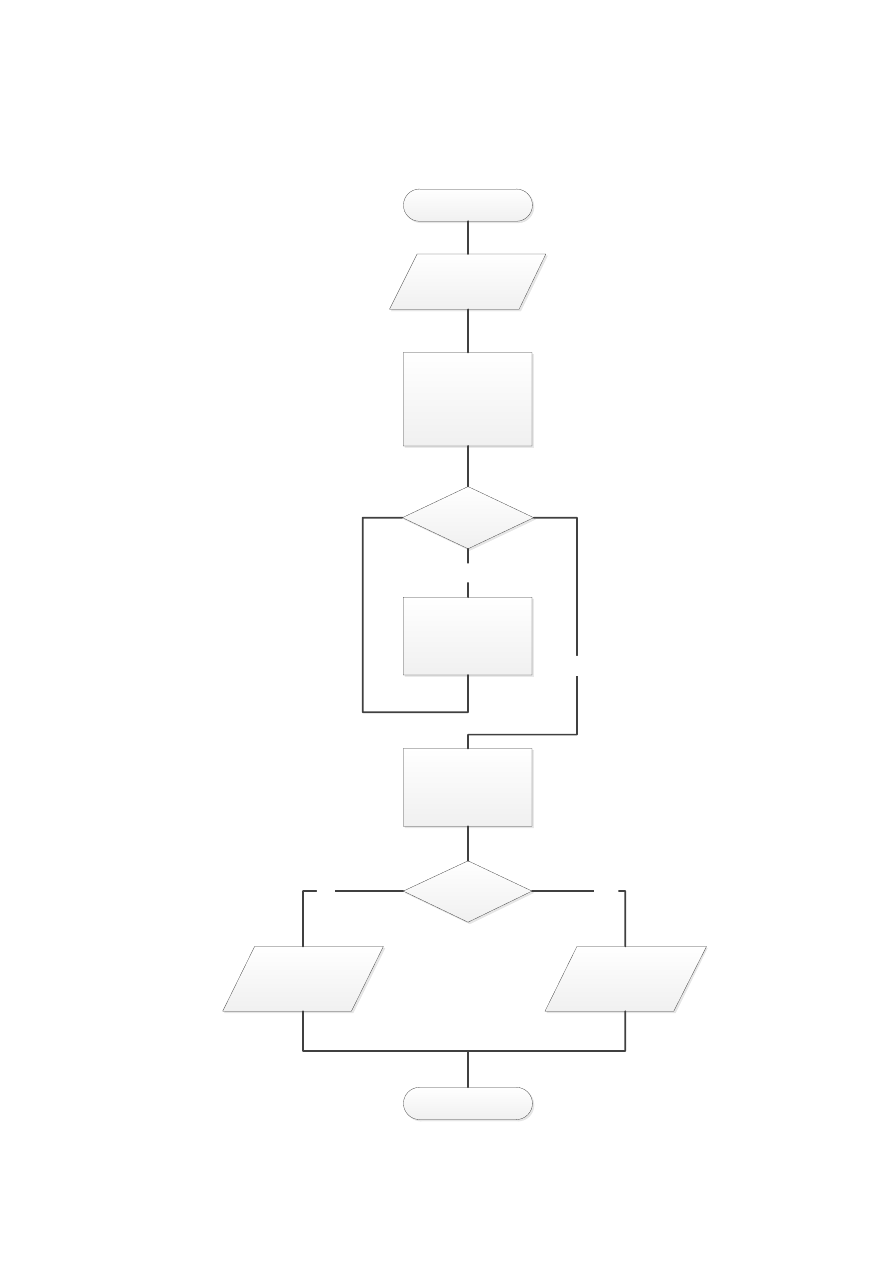
В данном разделе приводится алгоритм программы (рисунок 2),
осуществляющей решение поставленной задачи.
Начало
Ввод
l, k, m, R, r
h1
((Sz>=Su)&&
(k<=h2))
h2+=m;
Sz=p*r*(h1+h2+r+sqr
t(r*r+pow(((h2-h1)/
2), 2)));
max=h2+m;
S=p*r*(h1+(h2+m)+r+
sqrt(r*r+pow(((
(h2+m)-h1)/2),2)));
((S<=Su)&&
(max>=k))
Вывод
S, Su, max
Вывод
"Решения
нет!"
Конец
h2=l-m;
Su=4*p*R*R;
Sz=p*r*(h1+h2+r+sqr
t(r*r+pow(((h2-h1)/
2),2)));
Да
Нет
Да
Нет
1
2
3
4
5
6
7
8
9
10
Рисунок 2 – Алгоритм программы

21
Программа начинает свою работу с блока начало (1) после чего переходит
к блоку ввода данных (2), в ходе работы которого с клавиатуры вводятся
значения: l – начальное значение наибольшей высоты h
2
усеченного круглого
цилиндра; k– конечное значение наибольшей высоты h
2
усеченного круглого
цилиндра; m – шаг с которым изменяется значение наибольшей высоты; R –
радиус шара; r – радиус основания усеченного круглого цилиндра; h
1
–
наименьшая высота усеченного круглого цилиндра. После окончания работы
блока ввода данных (2) начинается работа блока действия (3), в котором:
наибольшей высоте h
2
присваивается начальное значение h
2
= l – m;
рассчитываются площадь поверхности шара S
u
по формуле S
u
= 4 * p * R * R и
площадь поверхности усеченного круглого цилиндра S
z
по формуле
S
z
= p * r (h
1
+ h
2
+
r + sqrt(r * r + pow(((h
2
– h
1
) / 2), 2)))
. Далее начинается работа
логического блока (4), этот блок проверяет данные на соответствие условиям:
площадь усеченного цилиндра S
z
не должна быть меньше площади шара S
u
и
наибольшая высота h
2
не должна быть меньше конечного значения k. Если
условия логического блока (4) выполняются, то программа переходит к
выполнению блока действия (5). Здесь наибольшей высоте h
2
присваивается
новое значение h
2
+= m, и рассчитывается площадь поверхности усеченного
круглого цилиндра S
z
= p * r (h
1
+ h
2
+
r + sqrt(r * r + pow(((h
2
– h
1
) / 2), 2)))
, после
чего программа снова переходит к работе логического блока (4). Если условия
логического блока (4) не выполняются, то программа переходит к выполнению
блока действия (6). В этом блоке присваивается максимальное значение
наибольшей высоты max = h
2
+ m и производится расчет соответствующей ей
площади поверхности усеченного круглого цилиндра S по формуле
S = p * r (h
1
+ (h
2
+ m) +
r + sqrt(r * r + pow((((h
2
+m) – h
1
) / 2), 2)))
. После этого
программа переходит к логическому блоку (7), в котором данные проверяются
на соответствие условиям: площадь поверхности усеченного круглого
цилиндра S не должна быть больше площади поверхности шара S
u
, а
максимальное значение наибольшей высоты max не должно быть меньше
конечного значения k. Если условия логического блока (7) выполняются, то
программа переходит к выполнению блока вывода данных (8), в котором на

22
экран выводятся значения: S – площадь поверхности усеченного круглого
цилиндра соответствующая максимальному значению наибольшей высоты; S
u
–
площадь поверхности шара радиуса R; max – максимальное значение
наибольшей высоты h
2
усеченного круглого цилиндра. Если условия
логического блока (7) не выполняются, то программа переходит к выполнению
блока вывода данных (9), в котором на экран выводится фраза «Решения нет!».
После этого программа завершает свою работу (10).

23
2.4 Анализ вычислений результатов
Расчеты, проведенные по программе, реализующей описанный в пункте
2.3 алгоритм (приложение А), позволили получить следующие результаты
(таблица 2).
Таблица 2 – Результаты программы
Номер
варианта
l
k
m
R
r
h
1
S
ц
S
ш
h
2
1
20,3
1,2
-0,1
2,4
1,8
0,9
70,8
72,3
6,5
2
24,4
10,6
-0,1
12,9
13,6
8,1
2081,3 2090,1
13,2
3
1,87
0,34
-0,01
0,52
0,39
0,2
3,36
3,39
1,4
4
12,2
7,1
-0,1
8,5
8,3
6,6
901,7
907,5
11,1
5
10,1
4,9
-0,1
19,3
24,7
3,2
4668,5 4678,5
7,5
Анализ этих результатов дает возможность сделать вывод, что
составленная программа позволяет правильно решить поставленную задачу
(рисунок 3 – 7).
Рисунок 3 – Результаты решения с набором значений варианта 1
Рисунок 4 – Результаты решения с набором значений варианта 2