ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Электроника
Добавлен: 23.10.2018
Просмотров: 11032
Скачиваний: 27

146
.
(
)
ЭР
k
I
I
w
ch
L
=
Беря
производную
,
находим
коэффициент
переноса
1
sec
.
w
h
w
L
ch
L
⎛ ⎞
χ =
=
⎜ ⎟
⎛ ⎞
⎝ ⎠
⎜ ⎟
⎝ ⎠
(4.18)
Формула
(4.18)
является
одной
из
фундаментальных
в
тео
-
рии
транзисторов
.
С
увеличением
толщины
базы
коэффициент
переноса
согласно
(4.18)
неограниченно
уменьшается
и
при
w
L
>
близок
к
нулю
,
т
.
к
.
неосновные
носители
успевают
реком
-
бинировать
в
базе
,
не
доходя
до
коллекторного
перехода
.
Поэто
-
му
в
транзисторе
,
как
уже
отмечалось
,
базу
делают
как
можно
более
тонкой
,
так
чтобы
всегда
выполнялось
условие
w
L
<< .
То
-
гда
,
разлагая
( )
ch z
в
ряд
с
точностью
до
трех
первых
членов
,
приходим
к
выражению
2
4
1
.
1
1
1
2
24
w
w
L
L
χ =
⎛ ⎞
⎛ ⎞
+
+
⎜ ⎟
⎜ ⎟
⎝ ⎠
⎝ ⎠
(4.19
а
)
Учитывая
,
что
второй
и
третий
члены
знаменателя
много
меньше
единицы
,
можно
пользоваться
приближением
:
2
1
1
.
2
w
L
⎛ ⎞
χ = − ⎜ ⎟
⎝ ⎠
(4.19
б
)
Заметим
,
что
для
расчета
коэффициента
переноса
второй
член
вообще
несущественен
(
независимо
от
режима
и
толщины
базы
),
поскольку
в
него
не
входит
эмиттерный
ток
.
Коэффициент
передачи
тока
α
согласно
(4.13)
получается
путем
умножения
любого
из
выражений
(4.18)
или
(4.19)
на
ко
-
эффициент
инжекции
.
Так
,
из
наиболее
строгого
выражения
(4.18)
следует
sec
,
w
h
L
⎛ ⎞
α = γ
⎜ ⎟
⎝ ⎠
(4.20)
а
приближенные
выражения
(4.19
а
)
и
(4.19
б
)
дают
соответствен
-
но
:
147
2
1
;
1
1
2
w
L
α =
⎛ ⎞
+ ⎜ ⎟
⎝ ⎠
(4.21
а
)
2
1
[1
].
2
w
L
⎛ ⎞
α ≈ γ − ⎜ ⎟
⎝ ⎠
(4.21
б
)
Несмотря
на
ряд
ограничений
,
общей
тенденцией
при
раз
-
работке
транзисторов
является
приближение
коэффициента
пере
-
дачи
α
к
единице
,
поскольку
при
этом
,
как
увидим
ниже
,
улуч
-
шаются
усилительные
свойства
транзистора
.
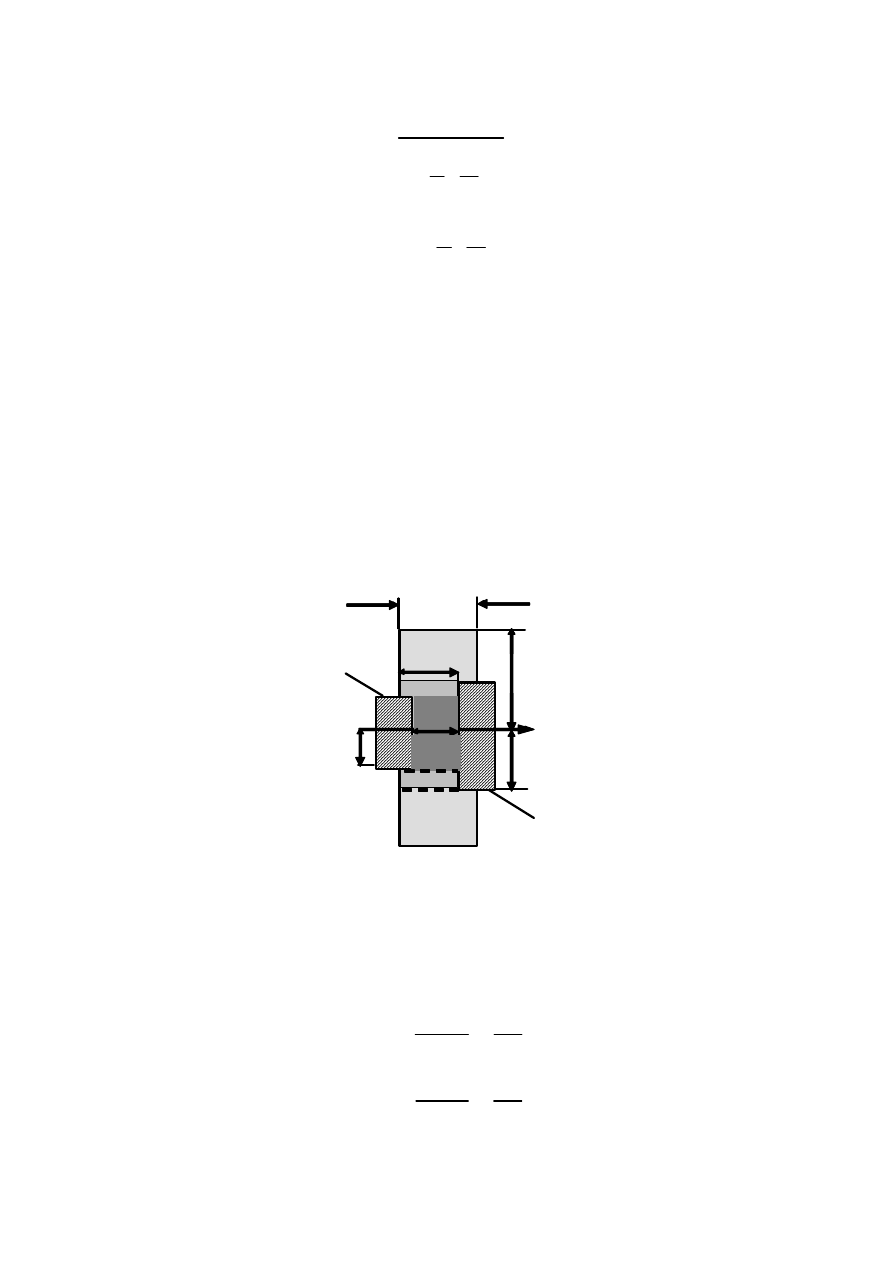
Объемное сопротивление базы.
Идеализируем
структуру
бездрейфового
транзистора
так
,
как
показано
на
рис
. 4.14.
Как
видим
,
базовый
ток
(
если
считать
,
что
он
протекает
от
центра
ба
-
зы
к
периферии
)
встречает
различные
сопротивления
на
трех
раз
-
ных
участках
.
Первый
—
внутренний
—
участок
(
активная
об
-
ласть
базы
)
является
диском
.
R
3
R
2
R
1
Б
К
Э
w
2
w
3
R
3
w
1
Рис. 4.14 — Идеализированная
структура транзистора
Сопротивления
колец
в
радиальном
направлении
выража
-
ются
формулами
:
2
2
2
1
ln
;
2
б
б
R
r
w
R
ρ
=
π
3
2
3
2
ln
,
2
б
б
R
r
w
R
ρ
=
π

148
где
Б
ρ —
удельное
сопротивление
базы
.
Сопротивление
диска
равно
:
( )
2
2
1
.
б
б
R
I
R
I
R
=
4.5
Динамические
параметры
транзистора
Барьерные емкости. Эти
емкости
не
имеют
особой
специ
-
фики
по
сравнению
с
емкостями
р-n
перехода
(
диода
)
и
могут
быть
рассчитаны
по
формулам
(2.82).
При
этом
,
как
уже
отмеча
-
лось
,
формула
(2.82
б
)
оказывается
неточной
при
сколько
-
нибудь
значительных
прямых
смещениях
.
Учитывая
,
что
при
прямом
смещении
на
переходе
барьерная
емкость
во
много
раз
меньше
диффузионной
,
ее
влиянием
можно
пренебречь
.
Относительно
емкости
Ск
нужно
заметить
,
что
она
представляет
собой
емкость
коллектора
,
соответствующую
активной
области
базы
.
Емкости
коллектора
,
соответствующие
промежуточной
и
пассивной
об
-
ластям
базы
,
могут
считаться
соединенными
параллельно
и
под
-
ключенными
между
внешними
электродами
коллектор
—
база
.
Эта
межэлектродная
емкость
часто
сравнима
с
величиной
Ск,
од
-
нако
при
расчетах
ее
можно
относить
к
нагрузке
транзистора
.
Необходимо
отметить
,
что
такое
утверждение
не
всегда
справед
-
ливо
и
зависит
от
конкретных
схемных
решений
.
Так
,
если
в
цепи
базы
транзистора
имеется
внешнее
сопротивление
,
то
эти
емко
-
сти
нельзя
считать
включенными
параллельно
нагрузке
.
Особый
интерес
при
анализе
переходных
и
частотных
ха
-
рактеристик
транзистора
представляет
коэффициент
передачи
тока
α
.
Поскольку
согласно
(4.13)
коэффициент
α
состоит
из
двух
множителей
—
коэффициента
инжекции
и
коэффициента
переноса
,
рассмотрим
эти
множители
раздельно
.
Коэффициент инжекции.
Напомним
,
что
ток
,
заряжающий
барьерную
емкость
Сэ,
образуется
основными
носителями
и
по
-
этому
не
передается
в
цепь
коллектора
.
Значит
,
увеличение
емко
-
стного
тока
на
высоких
частотах
равносильно
уменьшению
ко
-
эффициента
инжекции
:

149
.
1
СЭ
СЭ
Э
jX
w
jX
r
j
w
γ
−
γ
γ = γ
=
−
+
+
(4.22
а
)
Соответственно
изображение
коэффициента
инжекции
име
-
ет
вид
.
1
p
γ
γ
γ =
+ τ
(4.22
б
)
В
формулах
(4.30)
постоянная
времени
γ
τ
определяется
вы
-
ражением
1
.
Э Э
r C
w
γ
γ
τ =
=
(4.23)
Как
видим
,
частотные
и
переходные
свойства
коэффициента
γ
улучшаются
с
увеличением
рабочего
тока
,
так
как
при
этом
уменьшается
сопротивление
Э
r ,
а
увеличение
барьерной
емкости
эмиттерного
перехода
происходит
медленнее
.
У
дрейфовых
транзисторов
,
характерных
большими
рабо
-
чими
токами
и
меньшими
емкостями
,
частота
достигает
сотен
и
тысяч
мегагерц
,
и
частотные
свойства
коэффициента
передачи
тока
зависят
в
основном
от
коэффициента
переноса
,
поэтому
пе
-
рейдем
к
рассмотрению
α
.
Коэффициент передачи тока.
В
общем
случае
динамиче
-
ские
характеристики
коэффициента
α
определяются
коэффици
-
ентом
переноса
и
коэффициентом
инжекции
( )
sec ( ) 1
).
w
p
h
p
L
α
= γ
+ τ (4.24
а
)
Используя
приближение
,
можно
записать
:
( )
,
1
p
p
α
α
α
=
+ τ
(4.24
б
)
где
2
;
2
D
w
t
D
α
χ
τ = τ = χ ≈
(4.25
а
)
. .
. .
.
Э д Э д
С
r
α
τ =
(2.25
б
)
Оригиналом
изображения
(4.24
б
)
является
экспоненциаль
-
ная
функция
150
( )
(1
).
t
t
e
α
− τ
α
= α −
(4.26)
Частотная
характеристика
,
соответствующая
изображению
(4.24),
получается
заменой
оператора
p
на
jw
и
имеет
вид
.
1
w
J
w
α
α
α =
+
(4.27)
0.5
1
α
(t)/
α
0
0 1 2 3 4 5
1
2
t/t
D
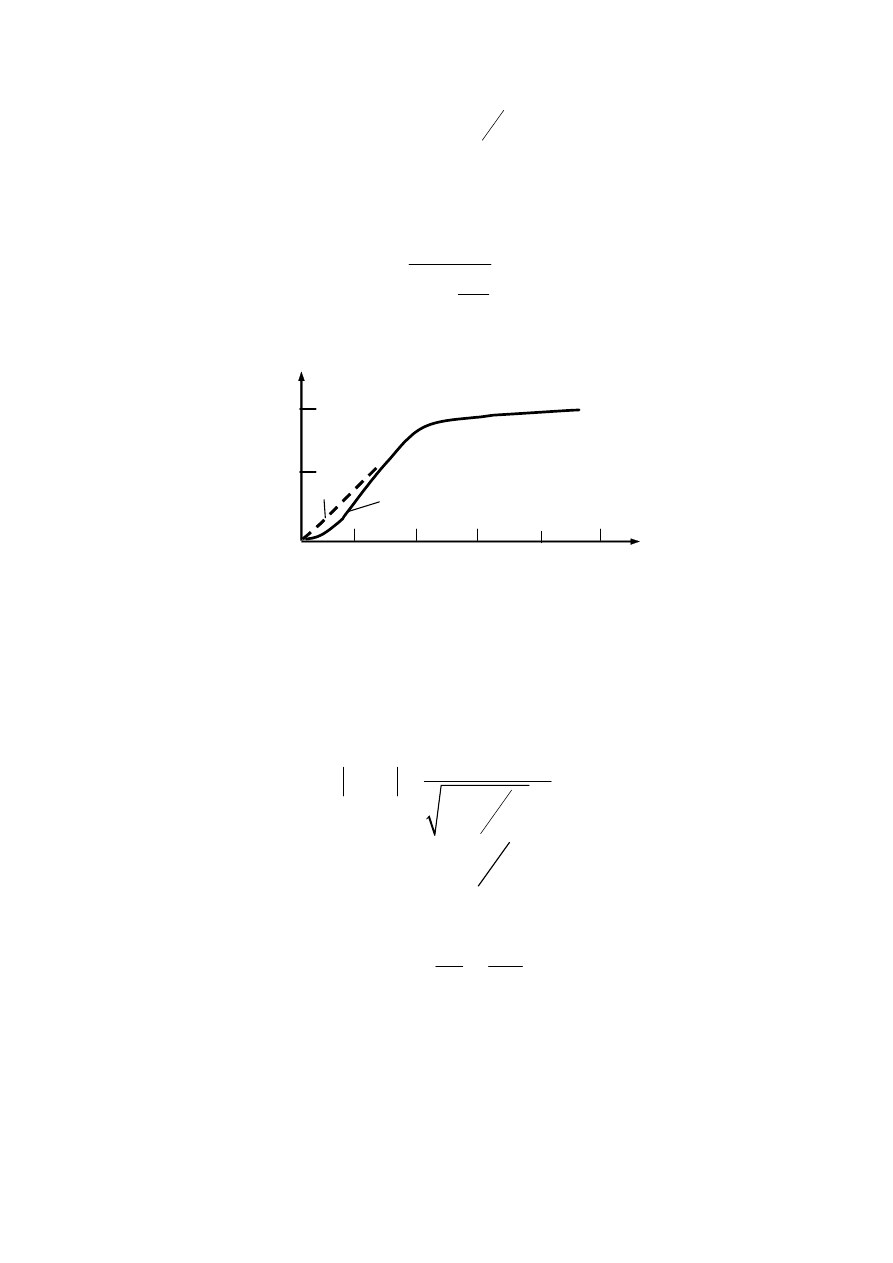
Рис. 4.15 — Переходные характеристики коэффициента
передачи: 1 — первое приближение; 2 — строгое решение
Амплитудно
-
частотная
и
фазочастотная
характеристики
легко
получаются
из
(4.27):
2
( )
;
1 (
)
w
w
w
α
α
α
=
+
(4.28
а
)
(
).
w
arctg
w
α
ϕ = −
(4.28
б
)
Граничная
частота
(
на
уровне
0,7)
равна
:
2
1
2
.
D
w
w
α
α
=
≈
τ
(4.29)
Изображение
(4.24)
и
связанные
с
ним
функции
(4.25) —
(4.27)
широко
используются
при
анализе
схем
,
если
задержка
фронта
и
сдвиг
фазы
не
играют
первоочередной
роли
.