ВУЗ: Алтайский Государственный Университет
Категория: Учебное пособие
Дисциплина: Аналитические методы в экономике
Добавлен: 23.10.2018
Просмотров: 618
Скачиваний: 5
Раздел 2. Моделирование процессов и процедур принятия решений, примеры.
Моделирование процессов и оптимальных решений. Многокритериальные модели принятия решений. Производственные функции. Задача оптимального среднесрочного планирования. Типовые задачи, решаемые с использованием инструмента Excel «Поиск решения».

Тема 2.1. Моделирование процессов и оптимальных решений. Многокритериальные модели принятия решений
2.1.1. Основные определения
В теории экономико-математического моделирования выделяют 2 основных класса математических моделей (модели процессов и модели решений), используемых в трех типах исследовательских задач:
-
оценка параметров экономических процессов и систем;
-
прогнозирование временных рядов и событий;
-
обоснование оптимальных решений.
Эти задачи можно выразить формулой активных (целенаправленных) действий: «знать», «предвидеть», «управлять». Отмеченная классификация математических моделей представлена на рисунке 2.1.1.

Полезно пользоваться определением математических (компьютерных) моделей. ММ это отражение в математических символах или в компьютерных операторах существенных сторон исследуемого явления или процесса.
Существует строгое различие математических и компьютерных моделей. Свойства математических моделей и получаемые с их использованием результатов исследуются строгим математическим аппаратом (методами). Компьютерные модели исследуются на ЭВМ.
2.1.2. Моделирование процессов
Структурно модели процессов представляют в виде «черного ящика» (рисунок 2.1).
Задача математического моделирования процессов при условии достаточно точных наблюдений за входными переменными и выходной переменной формулируется следующим образом:
Найти функцию
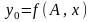 и доверительный интервал
и доверительный интервал
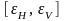 для
значений
для
значений
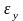 .(2.1)
.(2.1)
Тогда
на практике можно знать ожидаемые
значения выходной переменной при
известных значениях вектора
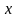 :
:
 .
.
Математическая модель (2.1) называется эмпирической (ЭМП), если основная информация для ее построения – результаты наблюдений моделируемого процесса или наблюдений за процессами – аналогами моделируемого, и теоретической (ТМП), если существенно используются знания соответствующей теории.
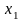
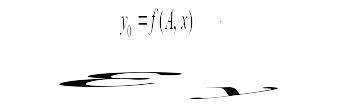
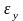
…
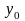
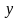
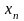
2.1.3. Моделирование решений
В данном месте следует пояснить объект моделирования, учитывая, что модель – отражение реальности. Конечным результатом модельных расчетов, является вариант решения, который предлагает аналитик. Но аналитик не несет ответственности за последствия принимаемого решения (кроме особых процедур страхования профессиональной ответственности). Кроме того, заказчик может дать задание аналитику предсказать решение конкурента в конкретной экономической ситуации.
В теории экономико-математического моделирования принято считать объектом моделирования лицо, принимающее решение (ЛПР). ЛПР – обобщенное и абстрактное понятие, в которое включено совокупность свойств реальных центров принятия решений, условий (экономических, финансовых, информационных, временных) в которых это решение формируется, границы зон ответственности решений, возможности (или невозможности) их корректирования и т.д. Реально решения могут приниматься с разной степенью рациональности в стандартных или в уникальных ситуациях.
В экономической литературе наиболее простым и часто используемым образом ЛПР выступает экономический человек1. Этим свойством наделяют субъектов экономической деятельности: не только отдельных людей, но и руководство предприятий, корпораций, органов государственного, местного самоуправления и стран в целом.
В
простом случае считается, что ЛПР знает
список возможных решений (математически
множество
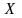 ),
полезность каждого решения (математически
функция
),
полезность каждого решения (математически
функция
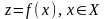 )
и выбирает оптимальное решение
)
и выбирает оптимальное решение
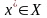 ,
которое имеет максимальную полезность.
,
которое имеет максимальную полезность.
Математически
модель решений (1 ЛПР) записывается так:
найти
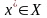 из условий2:
из условий2:
 . (2.2)
. (2.2)
В этом выражении
 или
или
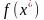 – значение оптимальной (максимальной)
полезности.
– значение оптимальной (максимальной)
полезности.
В настоящее время разработаны варианты математических моделей решений (1 ЛПР) в условиях ограниченной информированности (ЛПР не знает полного списка решений, ЛПР неточно оценивает полезности решений, информированность аналитика не совпадает с информированностью ЛПР). Основные подходы к построению таких моделей связаны с использованием теории вероятности (модели решений в условиях риска) и интервального (теоретико множественного) анализа (модели решений в условиях неопределенности).
2.1.4. Моделирование решений. Теория игр
На
рисунке 2.2.1 выделены математические
модели решений с n ЛПР
(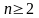 ),
которые используются для исследования
экономических систем с многими центрами
принятия решений. На практике трудно
разделить системы с одним и многими
центрами принятия решений. Но характерными
примерами систем с n ЛПР
выступают системы: «работник-работодатель»,
«контрольный орган-исполнитель»,
«товарный или финансовый рынки в условиях
конкуренции», «корпоративное управление»3.
),
которые используются для исследования
экономических систем с многими центрами
принятия решений. На практике трудно
разделить системы с одним и многими
центрами принятия решений. Но характерными
примерами систем с n ЛПР
выступают системы: «работник-работодатель»,
«контрольный орган-исполнитель»,
«товарный или финансовый рынки в условиях
конкуренции», «корпоративное управление»3.
Задачей аналитика при исследовании этих систем выступает построение математической (компьютерной) модели, с использованием которой можно предсказать решения всех ЛПР. Классической работой в данной области является книга Дж. фон Нейман, О. Моргенштерн, которая написана в США в 1944 г. На русском языке книга стала известной с 1970 г.4
Основные принципы математического моделирования экономических процессов и систем сохраняются и в рассматриваемой области. Дополнительными задачами выступают обоснование знаний всех ЛПР объекта моделирования о своих списках решений, целевых функциях, порядках ходов, об уровнях взаимной информированности и принятых правилах совестного выбора и реализации решений. Трудности математического моделирования связаны с наличием неполной информации об условиях выбора решений и о решениях, принимаемых другими ЛПР5.
2.1.5. Моделирование решений. Многокритериальные модели принятия решений
Рассматриваем
модели решений с одним ЛПР, которое
оценивает полезность решений вектором
показателей. Например эффект инвестиций
определяется их доходностью и уровнем
риска. При выборе варианта решения
необходимо найти компромисс между этими
критериями. В общем случае на множестве
решений
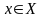 могут быть заданы n
(
могут быть заданы n
(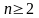 )
целевых показателей, часть которых
требуется минимизировать, а часть –
максимизировать. Без потери общности
можно считать, что все критерии следует
максимизировать6.
В теории экономико-математического
моделирования используют 2 подхода:
)
целевых показателей, часть которых
требуется минимизировать, а часть –
максимизировать. Без потери общности
можно считать, что все критерии следует
максимизировать6.
В теории экономико-математического
моделирования используют 2 подхода:
1. Свертка критериев, т.е. сведение многокритериальной задачи к однокритериальной задаче обоснования решений. Используют линейную и специальные нелинейные функции свертки частных критериев.
2. Выбор одного критерия в качестве ведущего и введение ограничения на уровни снижения значений по всем другим критериям.
Пример
2.1. Пусть задана задача принятия
решений с n (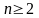 )
критериями
)
критериями
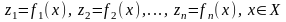 .
Введем интегральный критерий
.
Введем интегральный критерий
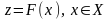 :
:
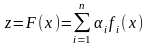 ,
где
,
где
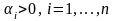 – «веса» частных критериев. Тогда
многокритериальная модель решения
сводится к модели (2.2) с целевой функцией
– «веса» частных критериев. Тогда
многокритериальная модель решения
сводится к модели (2.2) с целевой функцией
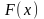 .
.
Задание 2.1. Ниже в разделе 3 приведена модель Марковица для поиска оптимального инвестиционного портфеля. Показать, что данная модель является двухкритериальной, а для поиска решения выбран подход 2, т.е. выбран ведущий критерий (какой?), а второй критерий (какой?) ограничен по значению.
Тема 2.2. Производственные функции
Производственная функция (также функция производства) — экономико-математическая количественная зависимость между величинами выпуска (количество продукции) и факторами производства, такими как затраты ресурсов, уровень технологий7.
Производственная функция является примером моделей процессов (часто это теоретическая модель процесса производства товаров и/или услуг). Рассматривается годовое количество произведенной фирмой продукции в стоимостной или натуральной форме. Факторами производства выступают объемы потребленных фирмой ресурсов (в стоимостном или в натуральном измерении). Главными ресурсами выступают потребленные за год количества труда и капитала8.
Определение.
Функция
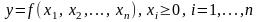 называется производственной, если
выполнены следующие ее свойства:
называется производственной, если
выполнены следующие ее свойства:
1. Нулевой выпуск в отсутствии одного или нескольких ресурсов.
2.
Неотрицательная производительность
факторов
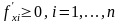 .
.
3.
Убывающая эффективность факторов
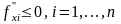 .
.
4.
Линейная однородность или постоянная
отдача от масштаба
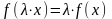 .
.
Примеры производственных функций:
1.
Классическая производственная функция
Кобба-Дугласа (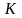 – амортизация капитала фирмы,
– амортизация капитала фирмы,
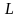 – фонд заработной платы за рассматриваемый
период времени):
– фонд заработной платы за рассматриваемый
период времени):
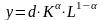 , (2.4)
, (2.4)
где
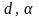 – параметры функции, индивидуальные
для фирмы (
– параметры функции, индивидуальные
для фирмы (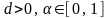 ).
).
2. Обобщенная функция Кобба-Дугласа:
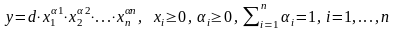 . (2.5)
. (2.5)
3. Линейная производственная функция:
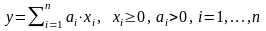 . (2.6)
. (2.6)
4. Производственная функция с нулевой эластичностью замещения ресурсов:
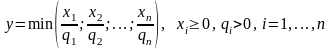 . (2.7)
. (2.7)
Задание 2.2. В записанных функциях укажите аргументы и параметры, поясните их экономический смысл и размерности.
Задание 2.3. Покажите, что функции (2.4) – (2.7) удовлетворяют определению производственных функций.
Тема 2.3. Задача оптимального среднесрочного плана развития производства
С использованием производственной функции рассмотрим задачу выбора оптимального соотношения запасов ресурсов. Эту задачу можно интерпретировать как задачу среднесрочного планирования развития фирмы.
Пусть
для некоторой фирмы известна
производственная функция, ее товарная
и ресурсная и технологическая политика
стабильна, а спрос на продукцию
неограничен. Пусть также в среднесрочной
перспективе заданы интервалы
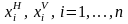 возможного изменения каждого из
существенных производственных ресурсов:
возможного изменения каждого из
существенных производственных ресурсов:
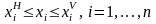 .
Тогда можно найти оптимальные значения
ресурсного обеспечения производства
решение следующей задачи. Найти
.
Тогда можно найти оптимальные значения
ресурсного обеспечения производства
решение следующей задачи. Найти
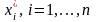 из условий:
из условий:
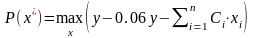 ; (2.8)
; (2.8)
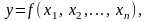
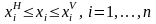 . (2.9)
. (2.9)
В
задаче (2.8) – (2.9)
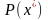 – оптимальная годовая прибыль
производственной деятельности фирмы
с учетом налога, равного 6% от выручки;
– оптимальная годовая прибыль
производственной деятельности фирмы
с учетом налога, равного 6% от выручки;
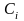 – цена ресурса i
(для ресурсов производства, учитываемых
в стоимостном измерении, их цена
принимается равной единице).
– цена ресурса i
(для ресурсов производства, учитываемых
в стоимостном измерении, их цена
принимается равной единице).
Можно показать (с учетом свойств производственной функции), что задача (2.8) – (2.9) относится к классу задач выпуклого программирования и ее решение можно получить в среде Excel.
Тема 2.4. Методы исполнения решений на различных этапах цикла принятия решений на примере задачи распределения ресурсов
На практике Центры принятия и реализации решений не являются идеально организованными и хорошо информированными. Тогда ожидаемые результаты не совпадают с реальными, особенно в ситуациях при больших по времени периодов реализации решений. Возникает необходимость совершенствования методических, математических и инструментальных методов принятия и реализации решений.
Выделим следующие этапы цикла принятия и реализации решений:
1. Сбор исходных данных и анализ экономической проблемы.
2. Обоснование оптимального решения и его принятие.
3. Реализация решения.
4. Оценка полученного результата и при необходимости внесение изменений в регламентные процедуры.
Характерным примером для данной темы является проблема распределения ограниченного ресурса. Она возникает в бюджетной сфере государственного и муниципального управления, производственных системах (корпорациях), при организации коллективных действий в социологии и политике и др.
Пусть
Центр располагает ограниченным ресурсом
в объеме
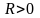 и ставит задачу его распределения по
и ставит задачу его распределения по
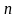 исполнителям так, чтобы суммарная
эффективность использования ресурса
была максимальной. Обозначим
исполнителям так, чтобы суммарная
эффективность использования ресурса
была максимальной. Обозначим
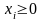 объем ресурса, выделяемого исполнителю
i (i=1,…,n).
Будем считать, что вклад
объем ресурса, выделяемого исполнителю
i (i=1,…,n).
Будем считать, что вклад
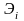 исполнителя i в
суммарную эффективность зависит от
объема выделенного ресурса и определяется
выражением:
исполнителя i в
суммарную эффективность зависит от
объема выделенного ресурса и определяется
выражением:
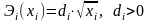 ,
где
,
где
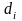 – коэффициент, истинное значение
которого Центр оценивает с погрешностью.
– коэффициент, истинное значение
которого Центр оценивает с погрешностью.
В
предположении, что Центр идеально
информирован, найдем оптимальное
распределение
 решением следующей задачи:
решением следующей задачи:
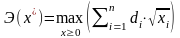 ; (2.10)
; (2.10)
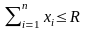 . (2.11)
. (2.11)
Задание
2.4. Доказать, что в рассматриваемой
формализации задачи при оптимальном
решении Центр распределяет весь объем
наличного ресурса и балансное ограничение
(2.11) выполняется как равенство:
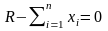
Решение
задачи (2.10) – (2.11) найдем с использованием
метода множителей Лагранжа (см. ссылку:
https://ru.wikipedia.org/wiki/Метод_множителей_Лагранжа).
Ограничение
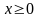 пока не рассматриваем. Запишем функцию
Лагранжа:
пока не рассматриваем. Запишем функцию
Лагранжа:
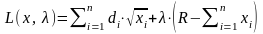 . (2.12)
. (2.12)
Составим
систему из (n+1)
уравнений, приравняв к нулю частные
производные функции Лагранжа по
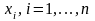 и по
и по
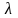 :
:
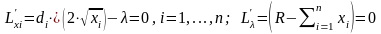 .
.
Найдем
решение первых n
уравнений записанной системы в зависимости
от
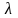 :
:
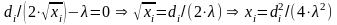 . (2.13)
. (2.13)
Рассматриваем последнее уравнение системы с учетом выражения (2.13):
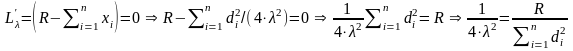 .
(2.14)
.
(2.14)
Из выражений (2.13) и (2.14) имеем:
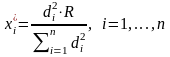 . (2.15)
. (2.15)
В рассматриваемом случае найденное
решение системы (n+1)
уравнений удовлетворяет ограничению
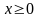 и является оптимальным распределением
ресурсов в задаче (2.10) – (2.11), поскольку
она относится к классу задач выпуклого
программирования.
и является оптимальным распределением
ресурсов в задаче (2.10) – (2.11), поскольку
она относится к классу задач выпуклого
программирования.
Рассмотрим порядок использования полученных расчетов на практике контроля процессов принятия и реализации решений, которое можно провести только после завершения цикла (после полной или частичной реализации решения). Для этого предлагается использовать расчетные и фактические значения эффективностей распределения и использования ресурсов. Профессиональное расследование эффективностей проводится с использованием методов экономической безопасности.