Регистры RG1, RG2 являются элементами памяти, предназначенными для запоминания и хранения исходных данных, промежуточных и окончательных результатов обработки данных операционным автоматом. Количество разрядов в регистре определяется разрядностью обрабатываемых данных и количеством разрядов, необходимых для промежуточного хранения признаков результата. Регистры могут быть последовательными/сдвиговыми (в этом случае данные в них вводятся/сдвигаются последовательно, бит за битом, от старшего/младшего бита к младшему/старшему), или параллельными (в этом случае данные в них вводятся параллельно во все разряды регистра). В некоторых случаях требуется универсальные регистры, в которых при различных кодах z_1R и z_2R данные могут сдвигать последовательно, в одном из направлений, параллельно или сдвиг данных в них может быть блокирован.

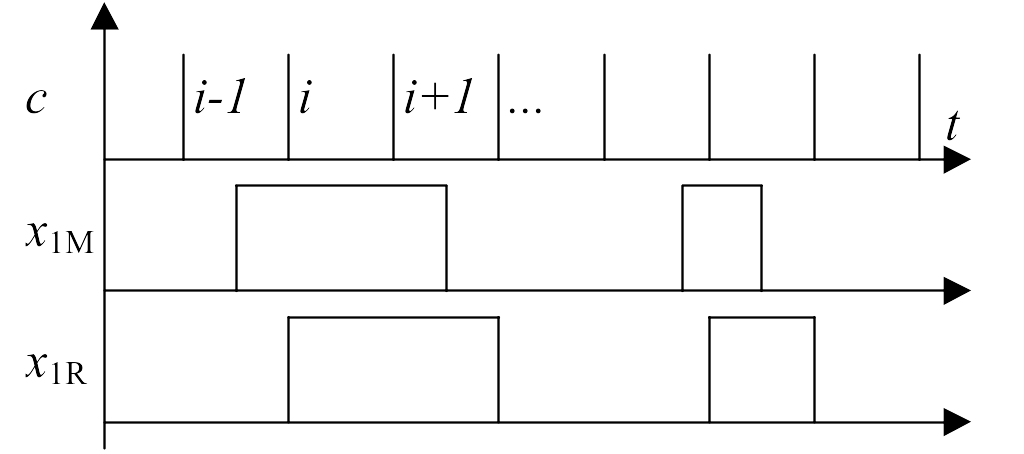
Существенным является тип триггера для реализации регистров. В курсовой работе принимается, что триггеры регистров тактируются фронтом, т.е. являются MS-триггерами (см. временную диаграмму, приведенную на рис. 3). Отметим, что регистры на триггерах JK и RS требуют подачи на их входы как самих регистрируемых кодов, так и их инверсных значений, что увеличивает аппаратные затраты на их реализацию.

Рис. 3. Процесс смены состояний на выходах регистров

в зависимости от состояний входов и сигнала тактирования

При синтезе операционного автомата необходимо:

определить состав комбинационных схем L1 - Ln, для каждой из комбинационных схем сформировать булево выражение, определяющее логику ее работы;

определить типы регистров для хранения данных;

определить количество направлений, с которых на входы регистров будут поступать данные;

определить разрядность данных каждого из направлений;

сформировать структурную схему операционного автомата;

определить разрядность данных, поступающих на каждый из функциональных блоков;

определить требования к составу и состояниям символов управления z и осведомительных символов и.

Результаты синтеза должны быть представлены в виде структурной схемы, таблицы состояний управляющих символов, таблицы состояний осведомительных символов в зависимости от результатов выполнения операций.

3.3. Общая методика синтеза управляющего автомата

Управляющий автомат проектируется на основании понятия абстрактного автомата. Существуют следующие схемы абстрактных автоматов.

Автомат Мили, или автомат первого рода, приведен на рис. 4. Он описывается следующей системой функций

w(t + 1) = L₁(u(t), q(t)); z(t) = L₂(u(t), q(t)),

где u(t) - управляющие символы; q(t) - внутреннее состояние автомата; w(t + 1) - следующее состояние автомата; z(t) - выходной символ.

В этом абстрактном автомате выдача символа z(t) происходит сразу, при старом значении внутреннего состояния q(t). Поэтому переход в новое состояние отстает по времени на один такт от изменения выходного символа. Это свойство автомата Мили поясняет рис. 4.

---

Рис. 4. Автомат Мили

Автомат Мура, или автомат второго рода, приведен на рис. 5. Он имеет функцию переходов такую же, как у автомата Мили, а функцию выходов, не зависящую непосредственно от входной переменной u(t).

Рис. 5. Автомат Мура

Система функций для автомата Мура имеет вид

w(t + 1) = L₁(u(t), q(t)); z(t) = L₂(q(t)),

Можно сказать, что у автомата Мура сначала меняется внутреннее состояние, и только после этого изменение состояния отражается на состоянии выходного символа. Функция выходов получается сдвинутой на один интервал времени.

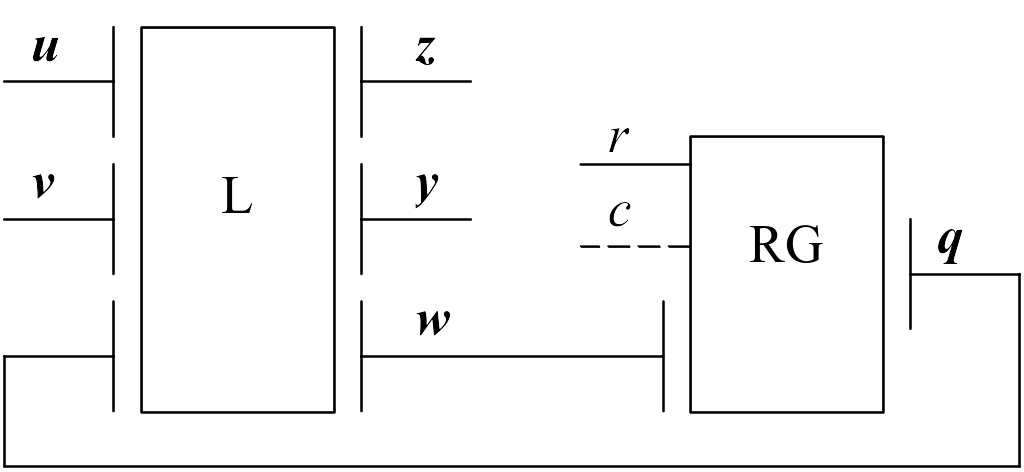
При проектировании управляющих блоков на практике чаще применяется более простая модель Мура. Функциональная схема управляющего автомата на базе абстрактного автомата Мура приведена на рис. 6.

Рис. 6. Функциональная схема управляющего автомата

На рис. 6 приведены следующие обозначения:

комбинационная схема L;

элемент памяти (регистр) RG;

вектор v внешних управляющих символов;

вектор у символов, несущих информацию о состоянии устройства;

вектор u осведомительных символов, поступающих с операционного автомата;

вектор управляющих символов z, подаваемых на операционный автомат;

вектор q текущих состояний управляющего автомата;

вектор w выходных символов комбинационной схемы (вектор возбуждения), формирующих очередное (следующее) состояние управляющего автомата;

r - сигнал сброса, переводящий управляющий автомат в исходное состояние;

с - сигнал тактирования управляющего автомата.

Вектор возбуждения w представляет собой совокупность структурных переменных, которые должны поступать на входы триггеров регистра RG, чтобы обеспечить их переключение в состояния, определенные алгоритмом функционирования автомата.

Комбинационная схема автомата (элемент L) объединяет все логические элементы, участвующие в формировании вектора управления z выходного вектора у и вектора возбуждения w на основании вектора осведомительных символов u, вектора внешнего управления v и вектора текущих состояний автомата q.

Проектирование управляющего автомата сводится к следующим этапам.

1. Составление алгоритма функционирования устройства управления.

2. По алгоритму функционирования определение количества состояний автомата.

3. Установление связей между состояниями автомата и значениями структурного вектора q.

4. Определение количества элементов памяти, необходимое для кодирования состояний автомата; число n элементов памяти равно количеству компонентов вектора q и должно отвечать условию n log₂ m, где m - число состояний заданного абстрактного автомата.

Соответствие между абстрактными обозначениями состояний и их структурными кодами устанавливается с помощью таблицы кодирования состояний. В простейшем случае это соответствие может быть выбрано произвольно.

Если входные и выходные переменные были заданы в абстрактном алфавите, то и для них должны быть решены вопросы кодирования с построением соответствующих таблиц. Практически это означает всего лишь возврат к струк­турным обозначениям, вытекающим из содержательных схем микропрограмм.

---

5. Выбор модели автомата, для формирования его структуры (определено заданием на курсовую работу).

6. Выбор базиса для реализации элементов памяти (триггеров регистра RG) и комбинационной схемы L.

7. Определение булевых функций для компонентов вектора w и приведение их к заданному базису.

Таким образом, каноническая методика сводит задачу синтеза автомата к синтезу логической схемы, формирующей систему функций возбуждения.

3.4. Составление алгоритма функционирования

управляющего устройства

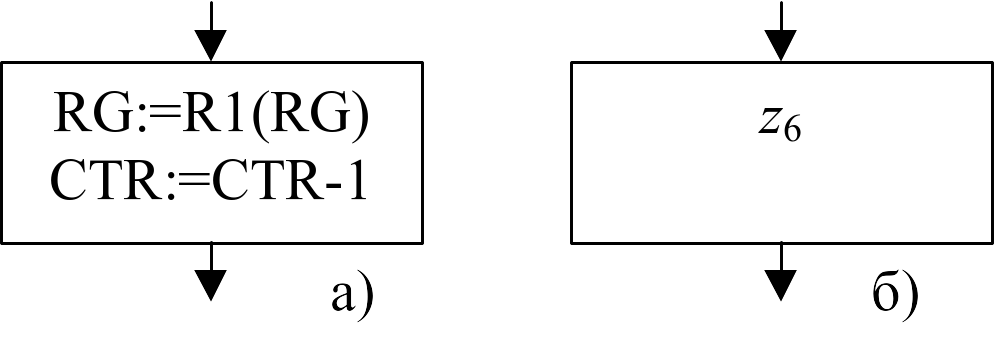
Алгоритм функционирования в курсовой работе должен быть представлен в виде блок-схемы. Алгоритм функционирования управляющего устройства, в основном, описан в задании на курсовую работу. Для синтеза управляющего автомата конкретный смысл процессов, следовательно, и конкретное содержание операторов алгоритма, не имеет значения, Поэтому содержательное описание операторов в алгоритме заменяется абстрактными обозначениями управляющих символов z (см. рис. 7). Следует отметить, что в алгоритме должен иметься оператор начала и оператор окончания. Перед попаданием алгоритма в оператор окончания на его выходе должен формироваться вектор признаков y выполнения алгоритма.

Рис. 7. Замена содержательного описания а)

операторов алгоритма абстрактным обозначением б)

Вектор z представляется в виде его отдельных составляющих: z = . Каждый такой символ z_i обозначает одну определенную микрокоманду, содержащую один или не­сколь­ко управляющих символов вектора z, и задает определенную совокупность одновре­мен­но выполняемых микроопераций.

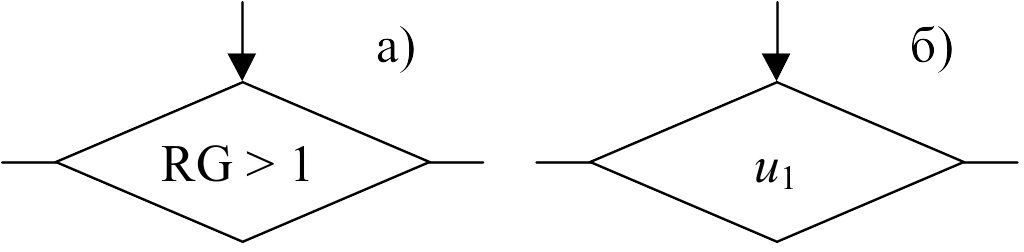
Входные структурные переменные вектора u, u₁, u₂, ... будем называть логическими условиями (ЛУ). Переход от содержательных обозначений логических условий (например, на языке функционального микропрограммирования) к структурным переменным поясняет рис. 8.

Рис. 8. Замена содержательного обозначения а)

управляющего оператора структурным обозначением б)

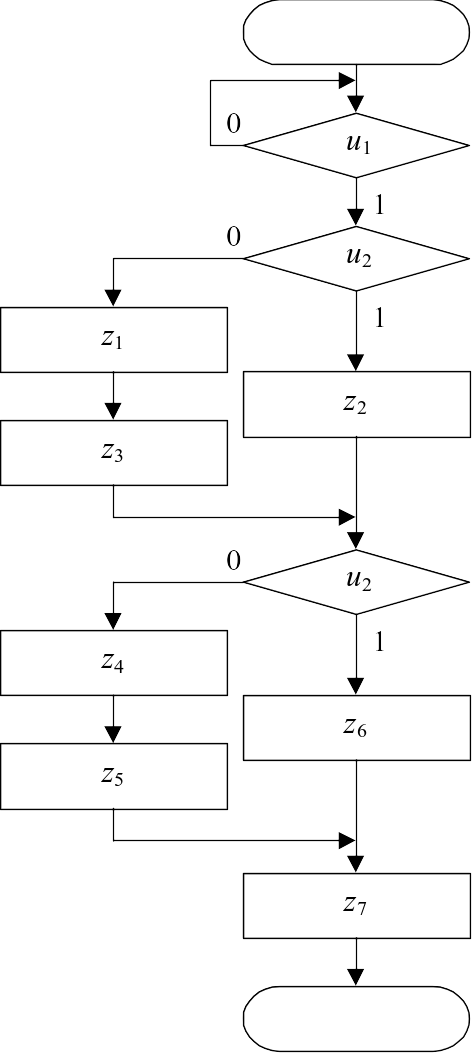
Содержательный смысл операторов и логические условия их выполнения устанавливается на подготовительном этапе синтеза на основе выданного задания. Смысл обозначений закрепляется таблицами. Пример результата составления блок-схемы алгоритма приведен на рис. 9.

Рис. 9. Блок-схема алгоритма

Следует отметить, что:

1. Управляющий оператор u₁ является ждущим оператором. Алгоритм запускается, когда u₁ = 1.

2. Оператор z_i, может означать управление параллельным выполнением нескольких микроопераций, если состав и структура операци­онного автомата позволяют это сделать. Указанные микрооперации выполня­ются за один такт, т.е. при одном состоянии управляющего автомата. Операторы z_i, z_j, расположенные в последовательно расположенных (сопряженных непосредственно, или через управляющие операторы) вершинах блок схемы, предполагают выполнение микроопераций последовательно, сначала подмножество микроопераций, заданных оператором z_i, а затем - подмножество микроопераций, заданных оператором z_j.

---

3. Если сопряженные операторы z_i, ..., z_j содержат одинаковые микрооперации, то указанные микрооперации должны выполняться столько раз, сколько раз они встречаются в кортеже (z_i, ..., z_j).

4. Одна и та же микрооперация не должна входить в один оператор дважды, при этом одинаковые микрооперации, выполненные одновременно различными компонентами операционного автомата, считаются различными микрооперациями.

В соответствии с блок-схемой алгоритма составляется матричная схема алгоритма, которая представляет квадратную таблицу с горизонтальными входами от z₀ до z_n со старшим (n) из имеющихся порядковых индексов и вертикальными - от z₁ до z_n+1. В клетки таблицы вписываются логические условия соответствующего перехода. Матричная схема алгоритма, приведенного на рис. 9, представлена в табл. 1.

Табл. 1

Матричная схема алгоритма

z₁ z₂ z₃ z₄ z₅ z₆ z₇ z₈

z₀ u₁ u₁u₂

z₁ 1

z₂

z₃

z₄ 1

z₅ 1

z₆ 1

z₇ 1

Следует отметить также одно важное свойство матричных схем алгоритмов: дизъюнкция содержимого всех кле­ток одной строки равна единице. Исключением является равенство дизъюнкции булевой переменной ждущего управляющего оператора (как это получилось в верхней строке табл. 1). Логическим условием безусловного перехода является константа, равная единице. Если по блок-схеме прослеживается несколько параллельных путей от оператора z_i к оператору z_j, то соответствующие логические условия должны записываться в клетки матричной схемы алгоритма через знак дизъюнкции.

На основании матричной схемы алгоритма составляются формулы перехода:

; ; ; ;

; ; ; .

Формулы отражают логические условия перехода в состояние, указанное после стрелки из состояний, указанного до стрелки. Если для перехода требуется выполнение нескольких условий, они должны включаться в формулу через конъюнкцию. Если в состояние, указанное после стрелки можно попасть из нескольких состояний, то они должны включаться в формулу через дизъюнкцию.

3.5. Кодирование состояний управляющего автомата

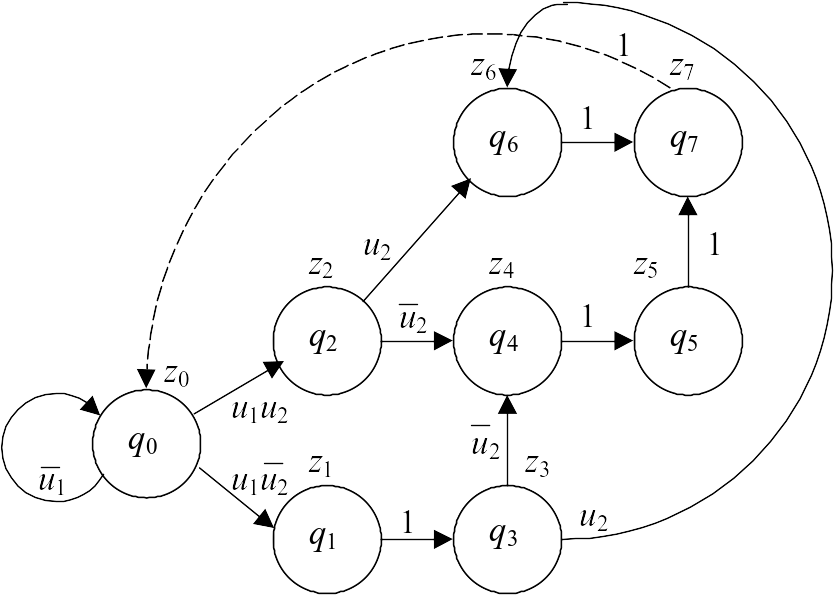
В соответствии с формулами перехода должен быть построен граф автомата Мура. Для алгоритма рис. 9 граф имеет вид, приведенный на рис. 10.

Рис. 10. Граф состояний автомата Мура

Следует различать внутренние состояния автомата Мура (на графе состояний они обозначены через q_i) и внешние управляющие символы (z_j).

В принципе, не существует правила, согласно которому определяют порядок следования кодов символов . Не существует также правил кодирования векторов u, v, w, z, y. При решении практических задач коды v, y могут оказаться заданными в технических требованиях на проектирования цифрового управляющего устройства, а коды u, z получаться естественным образом на выходах соответствующих блоков управляющего и операционного автомата (например, на выходе переполнения сумматора), или требоваться для управления соответствующим логическим устройством (например, при управлении выбора направления мультиплексора, или направления сдвига данных в регистре). Точно также и связь между кодами q и w для регистров, состоящих из разных типов триггеров, различна. Поэтому коды, определяемые в процессе проектирования должны быть такими, чтобы впоследствии можно было минимизировать комбинационную схему L, (см. рис. 6) преобразующую символы q, u, v в символы w, z, y.

---

В соответствии с выбранной системой кодирования одним из способов задаются булевы формулы, определяющие булевы функции переменных, составляющих символы w, z, y в зависимости от переменных, составляющих символы q, u, v. Булевы функции могут быть заданы одним из следующих способов: таблицей истинности; булевыми формулами, картой Карно (диаграммой Вейча).

При описании функций с помощью булевых формул рекомендуется использовать нормальную конъюнктивную (состоящую из элементарных дизъюн­к­ций, соединенных конъюнкциями) или нормальную дизъюнктивную (состоящую из элементарных конъюн­к­ций, соединенных дизъюнкциями) форму представления. Указанные формулы могут быть минимизированы с использованием следующих правил булевой алгебры.

1) Ассоциативность дизъюнкции и конъюнкции

; .

2) Коммутативность дизъюнкции и конъюнкции

; .

3) Существование нейтральных элементов для дизъюнкциии и конъюнкции

; .

4) Дистрибутивность конъюнкции относительно дизъюнкции и дизъюнкции относительно конъюнкции

; .

5) Закон исключенного третьего

.

6) Закон противоречия

.

7) Замкнутость множества {0, 1} относительно инверсии

.

8) Конъюнкция любой переменной с нулем равна нулю

0х = 0.

9) Идемпотентность дизъюнкции и конъюнкции

.

10) Правило поглощения

.

11) Правило склеивания

.

12) Правило де-Моргана

;

В результате минимизации нормальная дизъюнктивная или нормальная конъюнктивная форма булевых выражений должна сохраниться, т.к. указанные формы наиболее просто сводятся, соответственно к штриху Шеффера и стрелке Пирса.

По указанным выражениям должна быть построена структурная схема управляющего автомата, которая должна быть приведена в пояснительной записке к курсовой работе.

4. ОЦЕНКА КУРСОВОЙ РАБОТЫ

Защита курсовой работы проводится по одноступенчатой схеме, при этом общая оценка 100 баллов складывается из следующих оценок:

качество исполнения курсовой работы – до 35 баллов;

оценка рецензента – до 5 баллов;

качество доклада – до 20 баллов;

защита работы (ответы на вопросы) – до 40 баллов.

5. ЛИТЕРАТУРА

1. Ангер С. Асинхронные последовательностные схемы. - М.: Наука, 1977. - 400 с.

2. Баранов С.И. Синтез микропрограммных автоматов. - Л.: Энергия, 1979. - 231 с.

3. Голдсуорт В. Проектирование цифровых логических устройств. - М.: Машиностроение, 1985. - 288 с.

4. Закревский А.Д. Алгоритмы синтеза дискретных автоматов. - М.: Наука, 1971. - 511 с.

5. Зельдин Е.А. Триггеры. - М.: Энергоатом., 1983. - 95 с.

6. Карцев М.А., Брик В.А. Вычислительные машины и синхронная арифметика. - М.: Радио и связь, 1981. - 238 с.

7. Коршунов Ю.М. Математические основы кибернетики. -М.: Энергия, 1980. - 423 с.

8. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. - М.: Энергия, 1980. - 342 с.

9. Лазарев В.Т., Пийль Е.И. Синтез управляющих автоматов. -М.: Энергоатом., 1988. - 328 с.

10. Лысиков Б.Г. Арифматические и логические основы цифровых автоматов. - Минск: Вышейшая школа, 1980. - 335 с.

---

Смотрите также файлы

• Технологии программирования.docx

• Лабораторная 2.doc

• Основы инфокоммуникационны технологий.pdf

• Задание для теоретической части курсовой работы.pdf

• Методические указания по информатике.docx