ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.09.2019
Просмотров: 1234
Скачиваний: 1
10
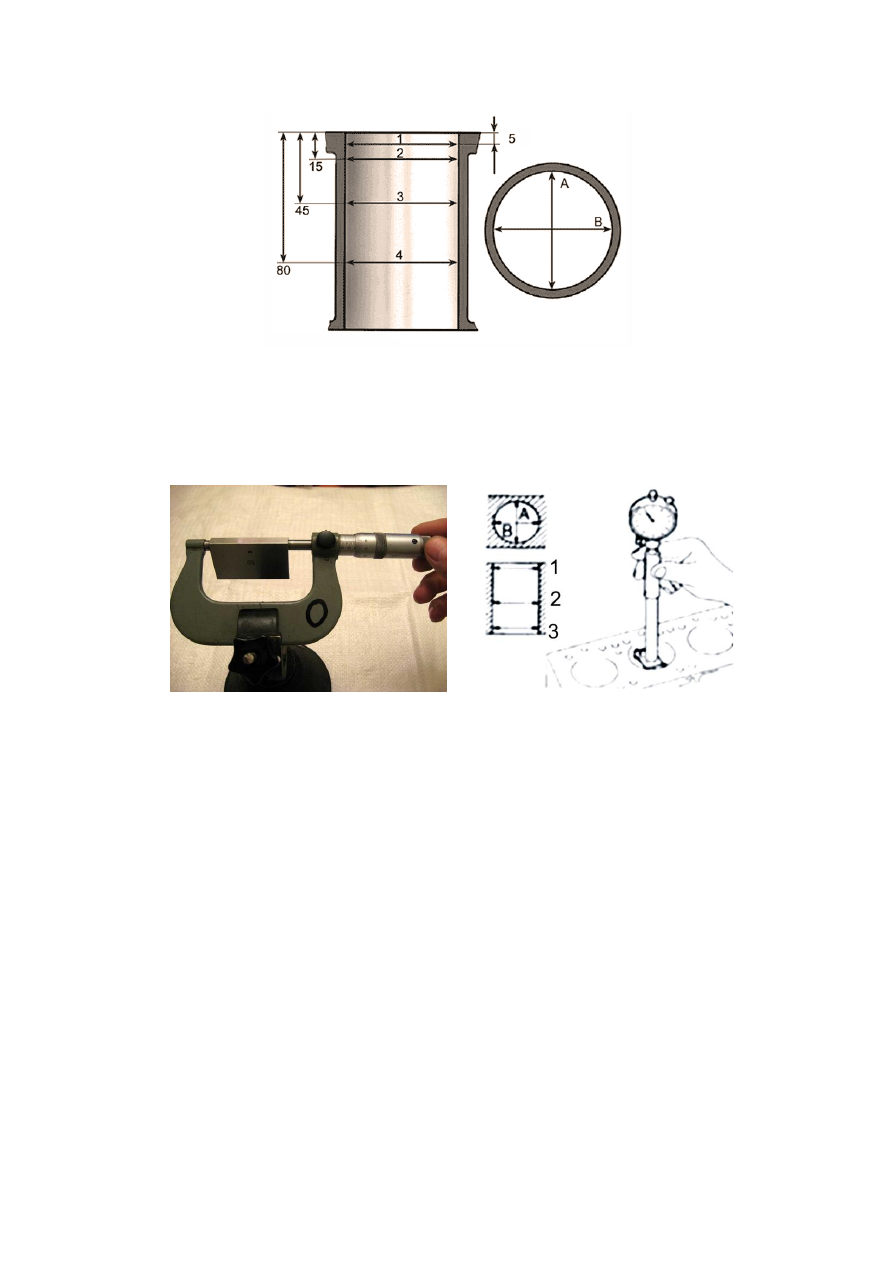
РиÑ. 2. ÐонÑÑÐ¾Ð»Ñ Ð·ÐµÑкала гилÑÐ·Ñ Ð¸ блока ÑилиндÑов
пÑи Ð¸Ñ Ð´ÐµÑекÑаÑии
Ðа
ÑиÑ. 3
Ð¿Ð¾ÐºÐ°Ð·Ð°Ð½Ñ Ð¿ÑÐ¸ÐµÐ¼Ñ Ð²ÑÐ¿Ð¾Ð»Ð½ÐµÐ½Ð¸Ñ ÑÐ°Ð±Ð¾Ñ Ð¿Ñи деÑекÑаÑии
гилÑз и блока ÑилиндÑов.
а)
б)
РиÑ. 3. ÐÑÐ¸ÐµÐ¼Ñ Ð²ÑÐ¿Ð¾Ð»Ð½ÐµÐ½Ð¸Ñ ÑÐ°Ð±Ð¾Ñ Ð¿Ñи деÑекÑаÑии гилÑз
и блока ÑилиндÑов: а â наÑÑÑойка микÑомеÑÑа на заданнÑй
ÑÐ°Ð·Ð¼ÐµÑ Ñ Ð¸ÑполÑзованием плиÑок;
б â Ð·Ð°Ð¼ÐµÑ Ð·ÐµÑкала ÑилиндÑа в блоке
ÐÐ»Ñ Ð¿ÑовеÑки ÑазмеÑов Ð³Ð»Ð°Ð´ÐºÐ¸Ñ ÑилиндÑиÑеÑÐºÐ¸Ñ , конÑÑнÑÑ , ÑезÑ-
бовÑÑ
и ÑлиÑевÑÑ
повеÑÑ
ноÑÑей деÑалей, вÑÑоÑÑ Ð²ÑÑÑÑпов и глÑбинÑ
впадин, еÑли на пÑовеÑÑемÑе ÑазмеÑÑ ÑÑÑÐ°Ð½Ð¾Ð²Ð»ÐµÐ½Ñ Ð´Ð¾Ð¿ÑÑки не ÑоÑ-
нее IT6 иÑполÑзÑÑÑ Ð¿ÑеделÑнÑе калибÑÑ.
ÐеÑодика ÑаÑÑеÑа велиÑÐ¸Ð½Ñ ÑемонÑного ÑазмеÑа
блоков и гилÑз ÑилиндÑов двигаÑелей
СпоÑоб воÑÑÑÐ°Ð½Ð¾Ð²Ð»ÐµÐ½Ð¸Ñ Ð¿Ð¾Ð´ ÑемонÑнÑй ÑÐ°Ð·Ð¼ÐµÑ Ð¿ÑедÑÑмаÑÑиваеÑ
обÑабоÑÐºÑ Ð¾Ð´Ð½Ð¾Ð¹ наиболее доÑогоÑÑоÑÑей и Ñложной ÑопÑÑженной
деÑали под ÑемонÑнÑй ÑазмеÑ, а дÑÑÐ³Ð°Ñ Ð·Ð°Ð¼ÐµÐ½ÑеÑÑÑ Ð½Ð¾Ð²Ð¾Ð¹ или воÑ-
11
ÑÑановленной Ñакже до ÑемонÑного ÑазмеÑа. ÐбÑабоÑкой под ÑемонÑ-
нÑй ÑÐ°Ð·Ð¼ÐµÑ Ð²Ð¾ÑÑÑанавливаÑÑ Ð³ÐµÐ¾Ð¼ÐµÑÑиÑеÑкÑÑ ÑоÑмÑ, ÑеÑоÑ
оваÑоÑÑÑ
и ÑоÑноÑÑнÑе паÑамеÑÑÑ Ð¸Ð·Ð½Ð¾ÑеннÑÑ
повеÑÑ
ноÑÑей деÑалей.
ÐоÑÑÑанавливаемÑе повеÑÑ Ð½Ð¾ÑÑи деÑалей могÑÑ Ð¸Ð¼ÐµÑÑ Ð½ÐµÑколÑко
ÑемонÑнÑÑ
ÑазмеÑов. ÐÑ
велиÑина и колиÑеÑÑво завиÑÑÑ Ð¾Ñ Ð²ÐµÐ»Ð¸ÑинÑ
изноÑа деÑали, пÑипÑÑка на обÑабоÑÐºÑ Ð¸ запаÑа пÑоÑноÑÑи деÑали.
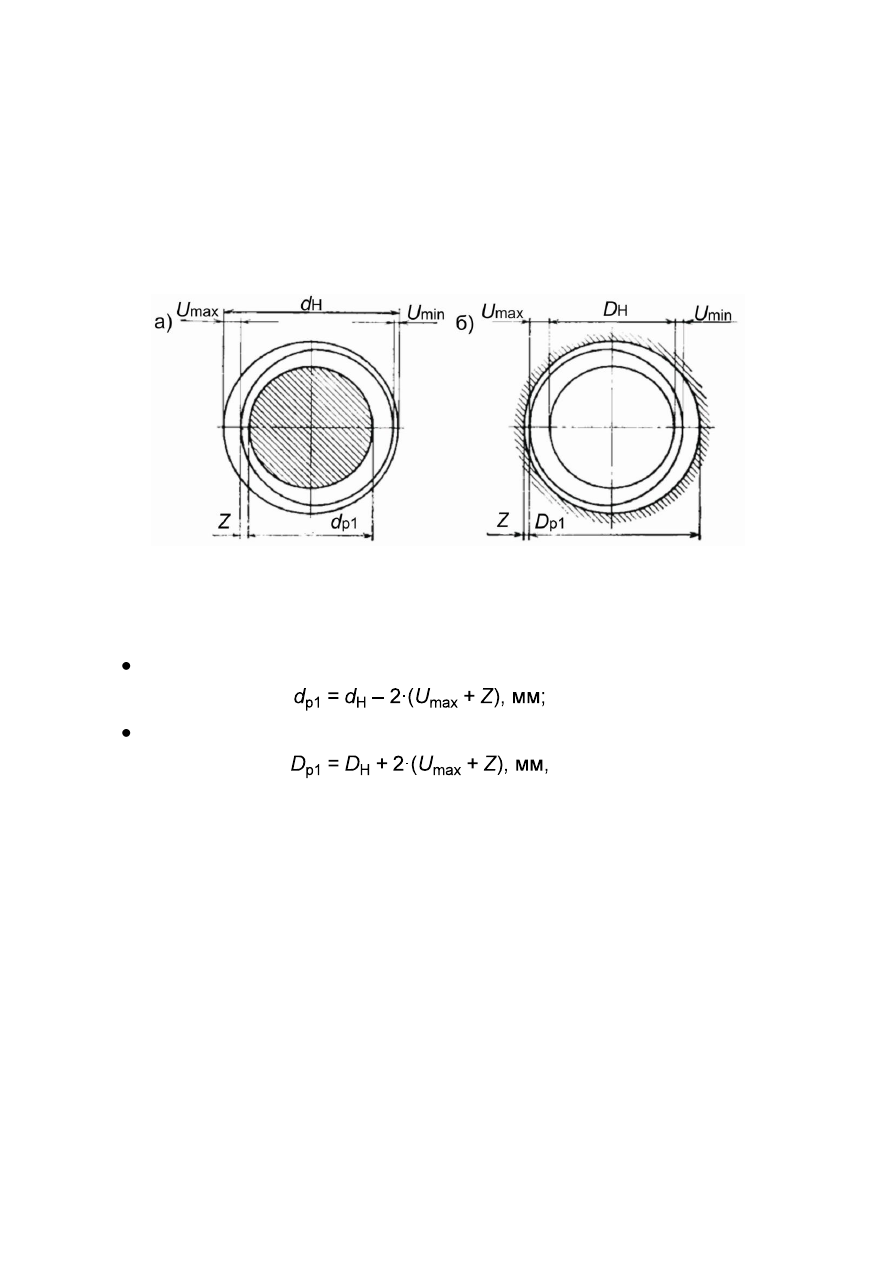
РиÑ. 4. Ð¡Ñ ÐµÐ¼Ð° Ð´Ð»Ñ Ð¾Ð¿ÑÐµÐ´ÐµÐ»ÐµÐ½Ð¸Ñ ÑемонÑнÑÑ ÑазмеÑов:
а â Ð´Ð»Ñ Ð²Ð°Ð»Ð°; б â Ð´Ð»Ñ Ð¾ÑвеÑÑÑиÑ
ÐеÑвÑй ÑемонÑнÑй ÑÐ°Ð·Ð¼ÐµÑ Ð¾Ð¿ÑеделÑеÑÑÑ Ð¿Ð¾ ÑоÑмÑлам:
Ð´Ð»Ñ Ð½Ð°ÑÑжнÑÑ ÑилиндÑиÑеÑÐºÐ¸Ñ Ð¿Ð¾Ð²ÐµÑÑ Ð½Ð¾ÑÑей (валов)
(1)
Ð´Ð»Ñ Ð²Ð½ÑÑÑÐµÐ½Ð½Ð¸Ñ ÑилиндÑиÑеÑÐºÐ¸Ñ Ð¿Ð¾Ð²ÐµÑÑ Ð½Ð¾ÑÑей (оÑвеÑÑÑий)
(2)
где
d
Ñ
1
и
D
Ñ
1
â пеÑвÑй ÑемонÑнÑй ÑÐ°Ð·Ð¼ÐµÑ ÑооÑвеÑÑÑвенно Ð´Ð»Ñ Ð²Ð°Ð»Ð°
или оÑвеÑÑÑиÑ, мм (
ÑиÑ. 4
);
d
Ð
и
D
н
â номиналÑнÑй ÑÐ°Ð·Ð¼ÐµÑ ÑооÑвеÑÑÑ-
венно Ð´Ð»Ñ Ð²Ð°Ð»Ð° или оÑвеÑÑÑÐ¸Ñ Ð¿Ð¾ ÑабоÑÐµÐ¼Ñ ÑеÑÑежÑ, мм;
U
max
и
U
min
â
ÑооÑвеÑÑÑвенно макÑималÑнÑй и минималÑнÑй Ð¸Ð·Ð½Ð¾Ñ Ð¿Ð¾Ð²ÐµÑÑ
ноÑÑи де-
Ñали на ÑÑоÑонÑ, мм;
Z
â пÑипÑÑк на Ð¼ÐµÑ Ð°Ð½Ð¸ÑеÑкÑÑ Ð¾Ð±ÑабоÑÐºÑ Ð½Ð° ÑÑо-
ÑонÑ, мм.
ÐÑи деÑекÑаÑии деÑалей обÑÑно замеÑÑÑÑ Ð½Ðµ велиÑÐ¸Ð½Ñ Ð¼Ð°ÐºÑи-
малÑного изноÑа
U
max
, а ÑÑммаÑнÑй Ð¸Ð·Ð½Ð¾Ñ Ð´ÐµÑали
U
на диамеÑÑ. Ðе-
ÑавномеÑноÑÑÑ Ð¸Ð·Ð½Ð¾Ñа ÑабоÑей повеÑÑ
ноÑÑи деÑали ÑÑиÑÑваеÑÑÑ ÐºÐ¾-
ÑÑÑиÑиенÑом β, коÑоÑÑй опÑеделÑеÑÑÑ Ð¸Ð· ÑооÑноÑÐµÐ½Ð¸Ñ Î² =
U
max
/
U
.
ÐÑи ÑиммеÑÑиÑном изноÑе деÑали, когда
U
max
=
U
min
=
U
/ 2
, коÑÑ-
ÑиÑÐ¸ÐµÐ½Ñ Ð½ÐµÑавномеÑноÑÑи изноÑа Ñавен β =
U
max
/
U
= 0,5. ÐÑи одно-
12
ÑÑоÑоннем изноÑе, когда
U
min
= 0,
U
max
=
U
, коÑÑÑиÑÐ¸ÐµÐ½Ñ Ð½ÐµÑавномеÑ-
ноÑÑи изноÑа Ñавен β =
U
max
/
U
= 1,0.
Таким обÑазом, знаÑÐµÐ½Ð¸Ñ ÐºÐ¾ÑÑÑиÑиенÑа неÑавномеÑноÑÑи изноÑа
изменÑÑÑÑÑ Ð² пÑÐµÐ´ÐµÐ»Ð°Ñ Î² = 0,5 â 1,0.
С ÑÑÑÑом коÑÑÑиÑиенÑа неÑавномеÑноÑÑи β и ÑÑммаÑной вели-
ÑÐ¸Ð½Ñ Ð¸Ð·Ð½Ð¾Ñа
U
на диамеÑÑ ÑоÑмÑÐ»Ñ Ð´Ð»Ñ ÑаÑÑÑÑа ÑемонÑного ÑазмеÑа
1 и 2 бÑдÑÑ Ð¸Ð¼ÐµÑÑ ÑледÑÑÑий вид:
Ð´Ð»Ñ Ð½Ð°ÑÑжнÑÑ ÑилиндÑиÑеÑÐºÐ¸Ñ Ð¿Ð¾Ð²ÐµÑÑ Ð½Ð¾ÑÑей (валов)
(3)
Ð´Ð»Ñ Ð²Ð½ÑÑÑÐµÐ½Ð½Ð¸Ñ ÑилиндÑиÑеÑÐºÐ¸Ñ Ð¿Ð¾Ð²ÐµÑÑ Ð½Ð¾ÑÑей (оÑвеÑÑÑий)
(4)
ÐелиÑина 2â(β
âU
+
Z
) =
j
в ÑоÑмÑÐ»Ð°Ñ 3 и 4 назÑваеÑÑÑ Ð¼ÐµÐ¶ÑемонÑ-
нÑм инÑеÑвалом. Таким обÑазом, ÑоÑмÑÐ»Ñ Ð´Ð»Ñ Ð¾Ð¿ÑÐµÐ´ÐµÐ»ÐµÐ½Ð¸Ñ ÑемонÑ-
нÑÑ
ÑазмеÑов в обÑем виде имеÑÑ ÑледÑÑÑий вид:
Ð´Ð»Ñ Ð½Ð°ÑÑжнÑÑ ÑилиндÑиÑеÑÐºÐ¸Ñ Ð¿Ð¾Ð²ÐµÑÑ Ð½Ð¾ÑÑей (валов)
(5)
Ð´Ð»Ñ Ð²Ð½ÑÑÑÐµÐ½Ð½Ð¸Ñ ÑилиндÑиÑеÑÐºÐ¸Ñ Ð¿Ð¾Ð²ÐµÑÑ Ð½Ð¾ÑÑей (оÑвеÑÑÑий)
(6)
где
n
â ÑиÑло ÑемонÑнÑÑ ÑазмеÑов;
j
â межÑемонÑнÑй инÑеÑвал.
ÐолиÑеÑÑво ÑемонÑнÑÑ ÑазмеÑов
n
опÑеделÑÑÑ Ð¿Ð¾ ÑÑловиÑм
пÑоÑноÑÑи деÑали, из конÑÑÑÑкÑивнÑÑ
ÑообÑажений или иÑÑ
Ð¾Ð´Ñ Ð¸Ð· ми-
нималÑно-допÑÑÑимой ÑолÑÐ¸Ð½Ñ ÑÐ»Ð¾Ñ ÑеÑмиÑеÑкой обÑабоÑки ÑабоÑей
повеÑÑ
ноÑÑи деÑали по ÑоÑмÑлам:
Ð´Ð»Ñ Ð½Ð°ÑÑжнÑÑ ÑилиндÑиÑеÑÐºÐ¸Ñ Ð¿Ð¾Ð²ÐµÑÑ Ð½Ð¾ÑÑей (валов)
(7)
Ð´Ð»Ñ Ð²Ð½ÑÑÑÐµÐ½Ð½Ð¸Ñ ÑилиндÑиÑеÑÐºÐ¸Ñ Ð¿Ð¾Ð²ÐµÑÑ Ð½Ð¾ÑÑей (оÑвеÑÑÑий)
(8)
где
d
min
и
D
max
â минималÑнÑй и макÑималÑнÑй ÑазмеÑÑ Ð´Ð¸Ð°Ð¼ÐµÑÑов
ÑооÑвеÑÑÑвенно вала и оÑвеÑÑÑиÑ.
ÐбÑабоÑкой деÑалей под ÑемонÑнÑй ÑÐ°Ð·Ð¼ÐµÑ Ð²Ð¾ÑÑÑанавливаÑÑ
гилÑÐ·Ñ Ð¸ блоки ÑилиндÑов двигаÑелей и дÑ. деÑали. Ð
Ñабл. 3
пÑиве-
13
Ð´ÐµÐ½Ñ ÑемонÑнÑе ÑазмеÑÑ Ð½ÐµÐºÐ¾ÑоÑÑÑ
деÑалей двигаÑелей ÑазлиÑнÑÑ
моделей.
ÐелиÑина пÑипÑÑка
Z
на Ð¼ÐµÑ Ð°Ð½Ð¸ÑеÑкÑÑ Ð¾Ð±ÑабоÑÐºÑ Ð·Ð°Ð²Ð¸ÑÐ¸Ñ Ð¾Ñ ÑÐµÑ -
ниÑеÑкого ÑоÑÑоÑÐ½Ð¸Ñ Ð¿Ð¾Ð´Ð²ÐµÑгаемой воÑÑÑÐ°Ð½Ð¾Ð²Ð»ÐµÐ½Ð¸Ñ Ð´ÐµÑали, вида ме-
Ñ
аниÑеÑкой обÑабоÑки, ÑпоÑоба ÑÑÑановки и кÑÐµÐ¿Ð»ÐµÐ½Ð¸Ñ Ð´ÐµÑали на
ÑÑанке, Ñипа обоÑÑÐ´Ð¾Ð²Ð°Ð½Ð¸Ñ Ð¸ его ÑоÑноÑÑи. ÐÐ¾Ð¶ÐµÑ ÑлÑÑиÑÑÑÑ, ÑÑо ка-
кой-либо из пеÑеÑиÑленнÑÑ
ÑакÑоÑов знаÑиÑелÑно ÑвелиÑÐ¸Ñ Ð²ÐµÐ»Ð¸ÑинÑ
пÑипÑÑка на обÑабоÑÐºÑ Ð¸ Ñогда воÑÑÑановление деÑали до ближайÑего
ÑемонÑного ÑазмеÑа бÑÐ´ÐµÑ Ð½ÐµÐ²Ð¾Ð·Ð¼Ð¾Ð¶Ð½Ð¾.
ÐлижайÑий ÑемонÑнÑй ÑÐ°Ð·Ð¼ÐµÑ Ð²Ð¾ÑÑÑанавливаемой ÑабоÑей по-
веÑÑ
ноÑÑи деÑали опÑеделÑеÑÑÑ ÑаÑÑÑÑом по ÑоÑмÑлам 3 и 4. Тогда
ÑооÑвеÑÑÑвенно Ð´Ð»Ñ Ð²Ð°Ð»Ð° и оÑвеÑÑÑÐ¸Ñ Ð¸Ð¼ÐµÐµÐ¼:
Ð´Ð»Ñ Ð½Ð°ÑÑжнÑÑ ÑилиндÑиÑеÑÐºÐ¸Ñ Ð¿Ð¾Ð²ÐµÑÑ Ð½Ð¾ÑÑей (валов)
(9)
Ð´Ð»Ñ Ð²Ð½ÑÑÑÐµÐ½Ð½Ð¸Ñ ÑилиндÑиÑеÑÐºÐ¸Ñ Ð¿Ð¾Ð²ÐµÑÑ Ð½Ð¾ÑÑей (оÑвеÑÑÑий)
(10)
ÐелиÑина
, завиÑÑÑÐ°Ñ Ð¾Ñ ÑакÑиÑеÑкого ÑоÑÑоÑÐ½Ð¸Ñ Ð¸Ð·Ð½Ð¾Ñен-
ной ÑабоÑей повеÑÑ
ноÑÑи опÑеделÑеÑÑÑ Ð¿ÑÑÑм замеÑов диамеÑÑа вала
или оÑвеÑÑÑÐ¸Ñ Ð¸ Ñавна:
Ð´Ð»Ñ Ð½Ð°ÑÑжнÑÑ ÑилиндÑиÑеÑÐºÐ¸Ñ Ð¿Ð¾Ð²ÐµÑÑ Ð½Ð¾ÑÑей (валов)
Ð´Ð»Ñ Ð²Ð½ÑÑÑÐµÐ½Ð½Ð¸Ñ ÑилиндÑиÑеÑÐºÐ¸Ñ Ð¿Ð¾Ð²ÐµÑÑ Ð½Ð¾ÑÑей (оÑвеÑÑÑий)
где
d
изм
и
D
изм
â ÑооÑвеÑÑÑвенно минималÑнÑй и макÑималÑнÑй заме-
ÑеннÑе ÑазмеÑÑ Ð¸Ð·Ð½Ð¾ÑеннÑÑ Ð´Ð¸Ð°Ð¼ÐµÑÑов Ð´Ð»Ñ Ð²Ð°Ð»Ð° и оÑвеÑÑÑиÑ.
ТаблиÑа 3
ÐоминалÑнÑе и ÑемонÑнÑе ÑазмеÑÑ Ð³Ð¸Ð»Ñз ÑилиндÑов
и блоков авÑомобилÑнÑÑ Ð´Ð²Ð¸Ð³Ð°Ñелей ÑазлиÑнÑÑ Ð¼Ð¾Ð´ÐµÐ»ÐµÐ¹, мм
ÐвÑÐ¾Ð¼Ð¾Ð±Ð¸Ð»Ñ Ð¸ моделÑ
двигаÑелÑ
ХаÑакÑеÑиÑÑика ÑазмеÑа
Ðоминал. 1 â Ñем.
2
â Ñем. 3 â Ñем.
1
2
3
4
5
ÐиÐ, ÐиÐ-508.10
100,0
+0,06
100,5
101,0
101,5
ÐÐÐ, ÐÐÐ-5233
92,0
+0,06
92,5
93,0
93,5
14
ÐÑодолжение Ñабл. 3
1
2
3
4
5
ÐÐÐ, ÐÐÐ-406
92,0
+0,06
92,5
93,0
â
ÐÐÐ, ÐÐÐ-2103, -07
76,0
+0,05
76,2
76,4
76,6
ÐÐÐ, ÐÐÐ-2106, -2121
79,0
+0,05
79,4
79,7
80,0
ÐÐÐ, ÐÐÐ-21083,
-09, -10
82,0
+0,05
82,4
82,8
-
ÐÐÐ, ÐÐÐ-1111
76,0
+0,05
76,4
76,8
â
ÐÐÐ, ÐÐÐ-11113
82,0
+0,05
82,4
82,8
â
УÐÐÐ-3317, -3313
85,0
+0,05
85,5
86,0
â
УÐÐÐ-331
82,0
+0,05
82,5
83,0
-
ÐоÑоÑикл «УÑал»,
Ð-63
78,0
+0,03
78,2
78,5
79,0
ÐоÑоÑикл Ð-650
«ÐнепÑ», ÐТ-8
78,0
+0,04
78,2
78,5
â
ÐÐÐÐÐ, ÐамÐÐ-740
120,0
+0,03
â
â
â
ЯÐÐ-850.10
130,0
+0,06
-
â
â
ЯÐÐ-236, 238
130,0
+0,04
130,25
+0,04
130,50
+0,04
â
ÐÑди, WH и WC
79,5
+0,01
79,7
80,0
80,5
ÐÑди, KP, KU и RT
81,0
+0,01
81,25
81,5
82,0
ÐÑди, NF
82,5
+0,01
82,75
83,0
â
Chrysler
, ÐÐС 242
0,076
0,025
98,4
98,7
â
â
ÐелиÑина пÑипÑÑка 2
Z
на Ð¼ÐµÑ Ð°Ð½Ð¸ÑеÑкÑÑ Ð¾Ð±ÑабоÑÐºÑ ÑиммеÑÑиÑнÑÑ
повеÑÑ
ноÑÑей (Ñел вÑаÑениÑ) опÑеделÑеÑÑÑ Ð¿Ð¾ извеÑÑной из ÑеоÑии
ÑаÑÑÑÑа пÑипÑÑков ÑаÑÑÑÑно-аналиÑиÑеÑким меÑодом ÑоÑмÑле:
(11)
где (
R
Z
+
T
)
i
â1
â велиÑина ÑлоÑ, ÑдалÑÐµÐ¼Ð°Ñ Ñ Ð¿Ð¾Ð²ÐµÑÑ Ð½Ð¾ÑÑи Ð´Ð»Ñ Ð¾Ð±ÐµÑпе-
ÑÐµÐ½Ð¸Ñ Ð·Ð°Ð´Ð°Ð½Ð½Ð¾Ð¹ ÑоÑноÑÑи и ÑеÑоÑ
оваÑоÑÑи воÑÑÑанавливаемой по-
веÑÑ
ноÑÑи;
i 1
â пÑоÑÑÑанÑÑвеннÑе оÑÐºÐ»Ð¾Ð½ÐµÐ½Ð¸Ñ Ð²Ð¾ÑÑÑанавливаемой
деÑали, завиÑÑÑие Ð¾Ñ ÐµÑ ÑеÑ
ниÑеÑкого ÑоÑÑоÑÐ½Ð¸Ñ (оÑÐºÐ»Ð¾Ð½ÐµÐ½Ð¸Ñ Ð¾Ñ Ð¿ÐµÑ-
пендикÑлÑÑноÑÑи, паÑаллелÑноÑÑи, ÑооÑноÑÑи воÑÑÑанавливаемÑÑ
по-
веÑÑ
ноÑÑей деÑали);
Ð
i
â погÑеÑноÑÑи, опÑеделÑемÑе ÑпоÑобом ÑÑÑа-
новки и кÑÐµÐ¿Ð»ÐµÐ½Ð¸Ñ Ð´ÐµÑали на ÑÑанке и ÑоÑноÑÑÑÑ Ð¾Ð±Ð¾ÑÑдованиÑ.
Тогда ÑоÑмÑÐ»Ñ 9 и 10 Ð´Ð»Ñ ÑаÑÑÑÑа ближайÑего ÑемонÑного Ñаз-
меÑа воÑÑÑанавливаемой ÑабоÑей повеÑÑ Ð½Ð¾ÑÑи деÑали пÑимÑÑ Ð²Ð¸Ð´: