Файл: Щапова 2016.pdf

116 

2)  уточнение  корней,  т.е.  вычисление  корней  с  заданной 

точностью на найденном отрезке [a,b]. 

Рассмотрим два метода решения второй задачи: метод про-

стых  итераций  (метод  последовательных  приближений)  и  ме-
тод бисекции (метод деления отрезка пополам). 

Метод простых итераций. Основным преимуществом это-

го метода является однотипность выполнения операций на каж-
дом  шаге,  что  в  значительной  степени  облегчает  составление 
программ. 

Задача  заключается  в  нахождении  корня  уравнения  вида 

( ) 0

f x

  на отрезке [a,b] с заданной точностью . 

Уравнение 

( ) 0

f x

   заменяется  равносильным  ему  урав-

нением вида 

( )

x

x

 

, что всегда можно сделать многими спо-

собами. 

Выберем  на  отрезке  [a,b]  начальное  приближение,  напри-

мер, 

0

,

2





a b

x

  и,  подставив  его  в  правую  часть  преобразован-

ного уравнения, вычислим следующее приближение к корню: 

1

0

( )

x

x

 

. 

Аналогично 

2

1

( )

x

x

 

, 

………. 

………. 

1

(

)

n

n

x

x



 

, 

т.е. каждое новое значение корня вычисляется через предыдущее 
по формуле 

1

(

)

i

i

x

x



 

.  

    (1) 

Процесс  последовательного  вычисления  значений  x

i

  по 

формуле (1) называется  итерационным  процессом  (процессом 
последовательных  приближений).  Окончание  итерационного 
процесса определяет условие достижения заданной точности 

: 

1

i

i

x

x





  . 

117 

Установлено,  что  предел  последовательности  x

1

,  x

2

, …, x

i

, 

если  он  существует,  является  корнем  уравнения  вида  ( ) 0

f x

 , 

т.е.  lim

i

i

x

x



 . 

Условием сходимости итерационного процесса, т.е. услови-

ем существования предела, является соблюдение неравенства 

( ) 1

x



 . 

Сходимость будет тем более быстрой, чем меньше величи-

на 

( )

x



, это необходимо учитывать при выборе функции 

(x). 

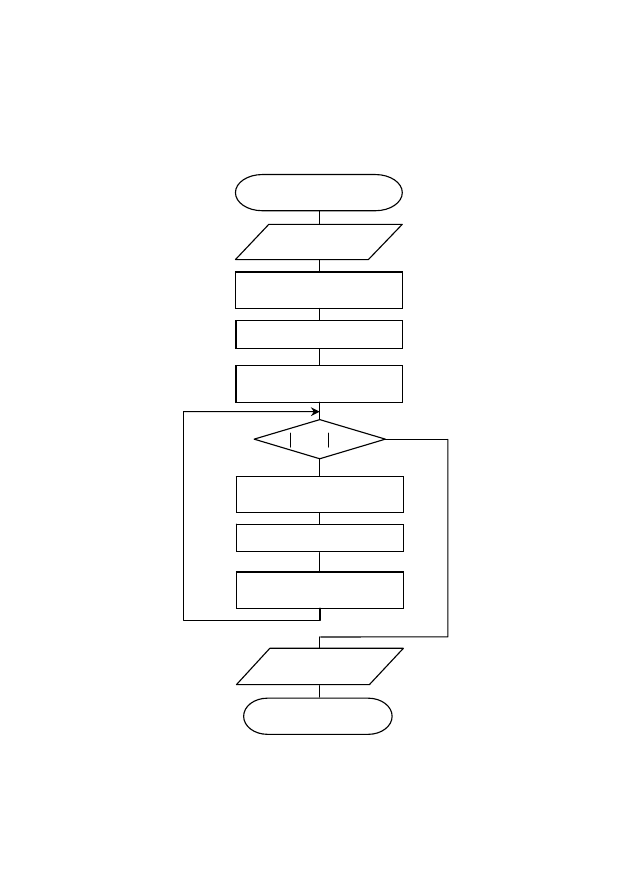
Блок-схема  алгоритма  нахождения  корня  уравнения  с  точ-

ностью 

  методом  итераций  приведена  на  рис. 17, где  x

0

  и  x

1 

– 

предыдущее  и  последующее  приближения  к  корню,  соответст-
венно, n – счетчик числа итераций. 

Метод бисекции. Решается уравнение вида  ( ) 0

f x

 . Счи-

таем, что  отделение  корней  произведено  и на отрезке  [a,b] рас-
положен  один  корень,  который  необходимо  уточнить  с  точно-
стью 

. Функция f(x) непрерывна на отрезке [a,b] и имеет разные 

знаки  на  его  концах,  т.е. 

( )

( ) 0

f a f b



 .  Если  непрерывная 

функция на отрезке меняет знак, то она на этом отрезке имеет по 
крайней мере одно нулевое значение (соответствующее значение 
x при этом и есть корень уравнения). 

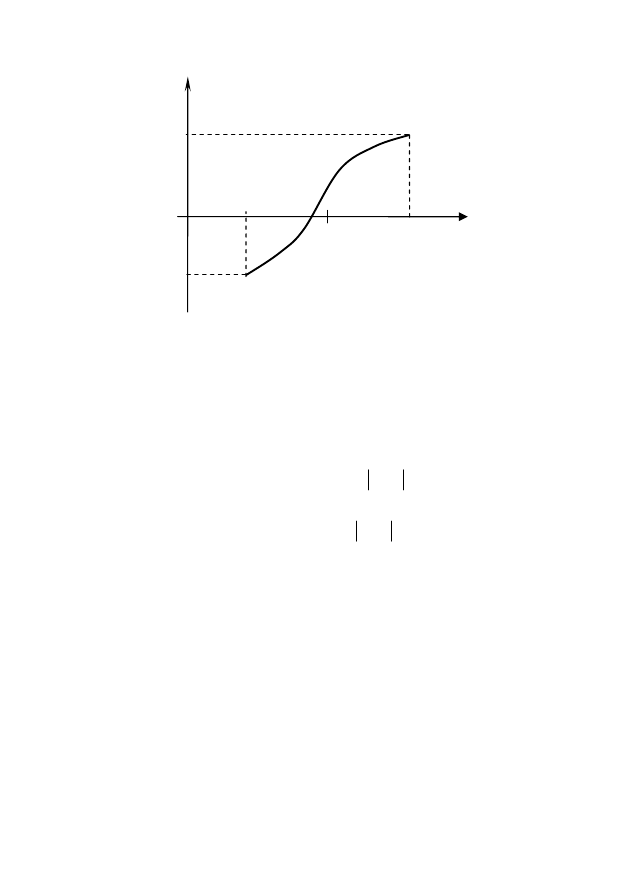
Для  нахождения  корня  отрезок  [a,b]  делится  пополам 

(рис. 18),  т.е.  выбирается  начальное  приближение  корня 

2

a b

x





. 

Вычисляем значение функции f(x) в точке x, и если оно рав-

но нулю или  ( )

f x

  , то это значение  x является корнем урав-

нения. 

Если  ( ) 0

f x

 , то выбирается тот из отрезков [a,x] или [x,b], 

на концах которого функция f(x) имеет противоположные знаки. 
Для  этого  проверяем:  если  условие  ( )

( ) 0

f a f x



 выполняется, 

то  выбираем  отрезок  [a,x],  а  если  не  выполняется,  то  отрезок 

118 

[x,b]. Для того чтобы отрезок снова можно было записывать как 
[a,b], необходимо сделать переприсвоение переменных: при вы-
полнении  условия  ( )

( ) 0

f a f x



   это  будет  b x

 ,  а  при  невы-

полнении – 

a

x



. 

Рис. 17. Блок-схема алгоритма нахождения корня уравнения 

с точностью 

 методом итераций 

Начало 

Ввод x

0

, 

 

n = 0 

х

1

 = φ(х

0

) 

n = n + 1 

1

0

x

x



 

x

0

 = x

1

n = n + 1 

да 

нет 

Вывод x

1

, n 

Конец 

х

1

 = φ(х

0

) 

119 

Рис. 18. Деление отрезка пополам  

для нахождения корня уравнения  

Полученный отрезок снова делится пополам, и повторяется 

то же рассмотрение. 

Процесс  деления  отрезков  пополам  продолжается  до  тех 

пор,  пока  не  будет  найдено  значение  корня  с  заданной  точно-
стью, т.е. пока не выполнится условие  ( )

f x

   или пока длина 

отрезка после очередного деления пополам не станет равной ли-
бо  меньше  заданной  точности,  т.е.  b a

   ,  и  тогда  корнем 

уравнения будет значение середины этого отрезка. 

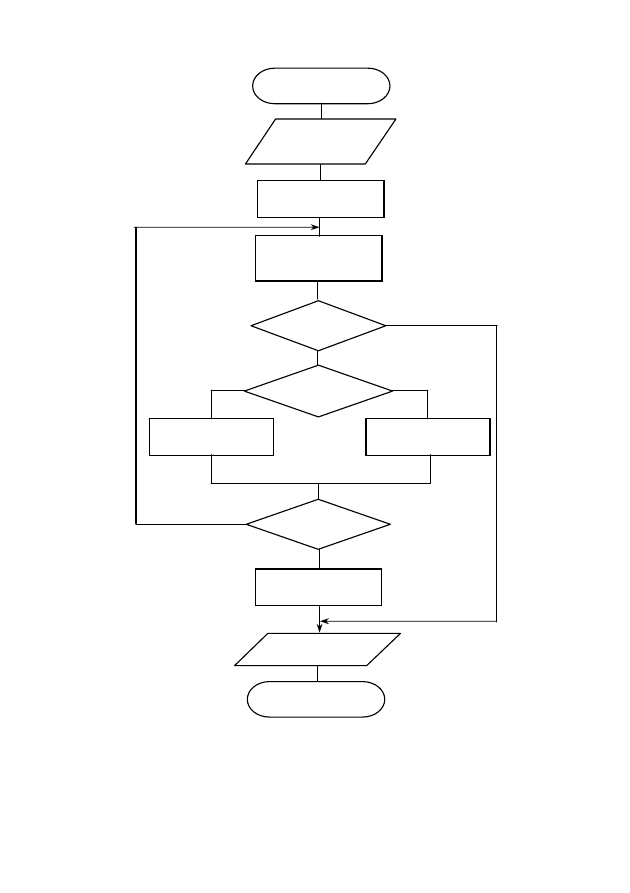
Блок-схема  алгоритма  нахождения  корня  уравнения  с  точ-

ностью 

 методом бисекции приведена на рис. 19. 

Решение систем линейных алгебраических уравнений.  

Метод Гаусса 

Метод Гаусса (метод последовательного исключения неиз-

вестных)  основан  на  приведении  матрицы  коэффициентов 
к треугольному  виду,  из  которой  затем  определяются  значения 
неизвестных. 

x 

y 

y = f(x) 

b 

a 

f(b) 

f(a) 

x 

120 

Рис. 19. Блок-схема алгоритма нахождения корня уравнения 

с точностью 

 методом бисекции 

Начало 

Ввод 

a, b, 

 

x = (a + b)/2 

F = f(x) 

a = x, F

1 

= F 

F

1 

= f(a) 

x = (a + b)/2 

b = x 

|b – a| 

 

нет 

да 

Вывод x 

Конец 

|F| > 



да 

F

1

F < 0

да 

нет 

нет