ВУЗ: Пермский национальный исследовательский политехнический университет
Категория: Учебное пособие
Дисциплина: Информатика
Добавлен: 25.10.2018
Просмотров: 10318
Скачиваний: 105
126
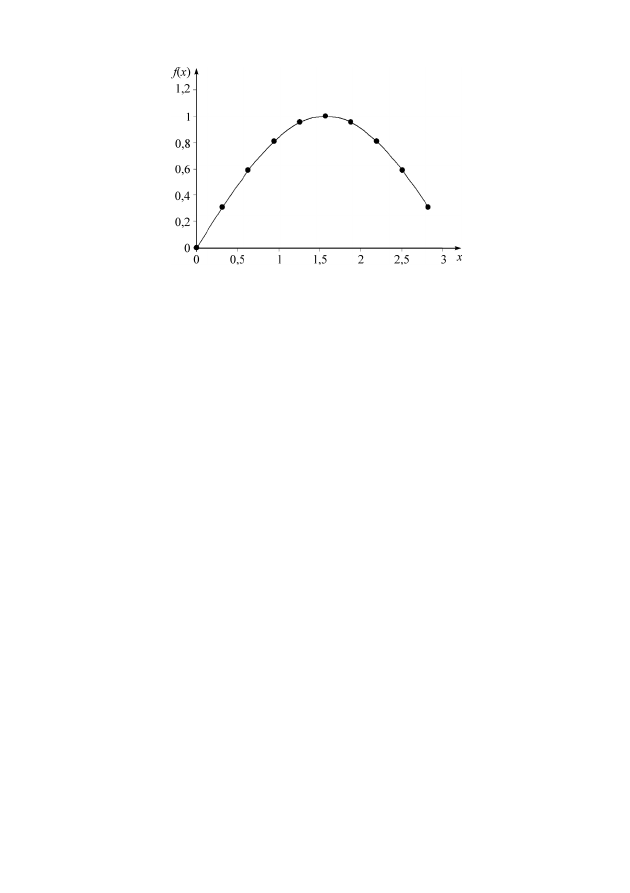
Рис. 26. Построение интерполирующей функции по дискретному
набору исходных табличных данных: ● – исходные табличные данные;
–– интерполирующая функция f(x)
Зависимость (5) полностью определена и может быть ис-
пользована для вычисления y при любых
[ , ]
x
a b
, если извест-
ны a
0
и a
1
. Подставив в (5) координаты точек (x
i
,y
i
) и (x
i+1
,y
i+1
),
получим систему уравнений для нахождения a
0
и a
1
0
1
0
1
1
1
,
.
i
i
i
i
a
a x
y
a
a x
y
Интерполяция алгебраическим многочленом для набора то-
чек (x
i
,y
i
), i = 1,2,…,n + 1 отрезка [a,b] – построение многочлена
P
n
(x) степени не выше n, который записывается в виде
1
1
1
0
( )
...
.
n
n
n
n
n
P x
a x
a
x
a x a
y
(6)
Значения a
0
, a
1
, …, a
n
, при которых многочлен (6) проходит
через все заданные точки, могут быть получены из решения сис-
темы уравнений, каждое из которых записывается для узла ин-
терполяции:
1
1
1
1
1
1
0
1
1
2
1
2
1
2
0
2
1
1
1
1
1
1
0
1
...
,
...
,
........................................................
...
.
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
a x
a
x
a x
a
y
a x
a
x
a x
a
y
a x
a
x
a x
a
y
(7)
127
Решение системы линейных уравнений (7) относительно не-
известных a
0
, a
1
, …, a
n
может быть выполнено методом Гаусса.
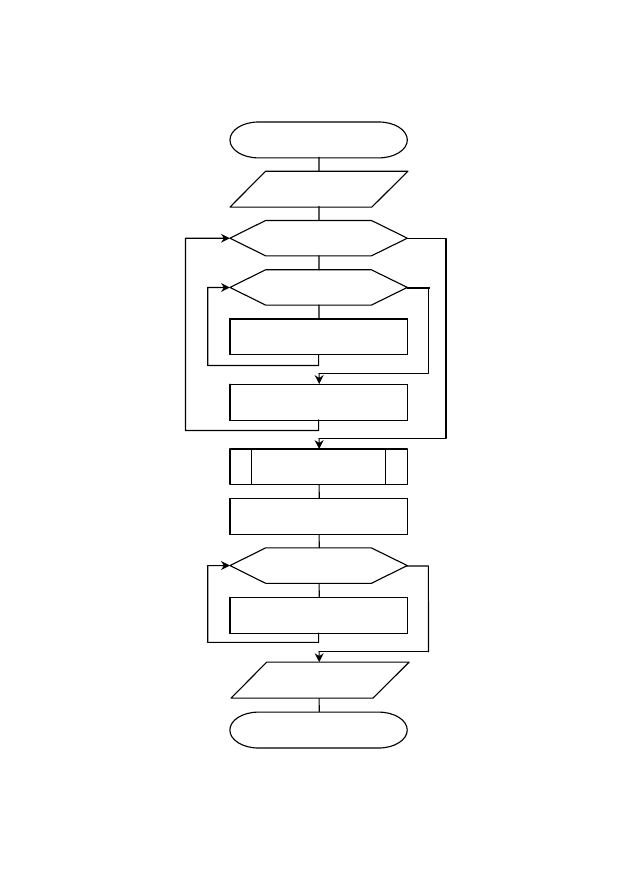
Рис. 27. Блок-схема алгоритма решения задачи интерполяции
(интерполяция алгебраическим многочленом)
Начало
Ввод n, z,
x(n + 1), y(n + 1)
i = 1, n + 1
j = 1, n + 1
k = n – j + 1
a
ij
= x
i
k
b
i
= y
i
Метод Гаусса
yz = 0
i = 1, n + 1
k = n – i + 1
yz = yz + b
i
z
k
Вывод
b(n + 1), z, yz
Конец

128
Блок-схема алгоритма решения задачи интерполяции алгеб-
раическим многочленом приведена на рис. 27, где a
ij
– матрица
коэффициентов системы уравнений; b
i
– вектор свободных чле-
нов, векторы x и y – исходные табличные данные; z – значение
аргумента x, для которого вычисляется промежуточное значение
функции yz после нахождения коэффициентов многочлена.
В результате выполнения приведенного на рис. 27 алгоритма
получаем a
n
= b
1
, a
n–1
= b
2
, …, a
0
= b
n+1
.
Аппроксимация табличных зависимостей
Под аппроксимацией (приближением) понимается замена
одних объектов (зависимостей) другими, близкими к исходным,
но более простыми.
Аппроксимация применяется при обработке результатов
измерений для получения простых приближенных формул, оп-
ределяющих зависимость между табличными данными.
В задачах интерполяции требовалось, чтобы искомая зави-
симость
( )
y
f x
совпадала со значениями таблично заданной
функции
( ),
1,2,...,
i
i
y
f x i
n
в узлах интерполяции.
На практике часто бывает, что аналитическое выражение
такой зависимости получить невозможно или очень сложно.
В этом случае решается задача аппроксимации, т.е. задача нахо-
ждения такой достаточно простой функции, значения которой на
отрезке [a,b], содержащем узлы интерполяции
,
1, 2,...,
i
x i
n
,
возможно, мало отличаются от значений таблично заданной
функции (рис. 28).
Для решения задачи аппроксимации необходимо выбрать
вид аппроксимирующей функции исходя из анализа графическо-
го представления
( ),
1,2,...,
i
i
y
f x i
n
, а затем по исходным
данным определить значения ее параметров.
Аппроксимирующая функция может быть представлена ги-
перболической, экспоненциальной, логарифмической или степен-
ной зависимостью, а также многочленом P
m
(x) степени m вида
2
0
1
2
( )
...
.
m
m
m
P x
a
a x a x
a
x
y
(8)
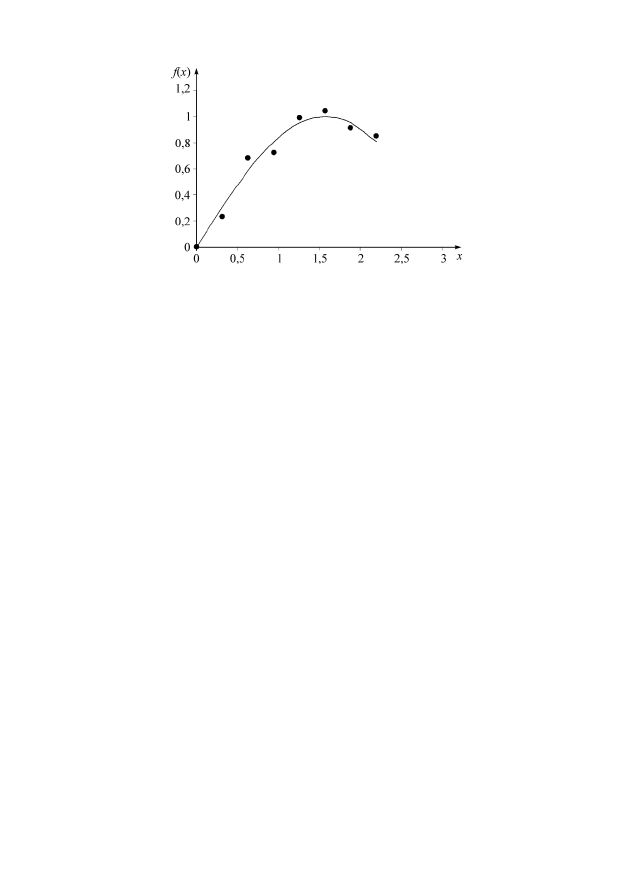
129
Рис. 28. Построение аппроксимирующей функции по дискретному
набору исходных табличных данных: ● – исходные табличные данные;
–– аппроксимирующая функция f(x)
Для определения параметров a
0
, a
1
, …, a
m
зависимости (8)
по исходным данным x
i
, y
i
, i = 1,2,…,n широкое распространение
получил метод наименьших квадратов. При этом степень мно-
гочлена m обычно принимается меньшей числа узлов интерпо-
ляции, т.е.
m n
.
При аппроксимации данных методом наименьших квадра-
тов определяют такие значения a
0
, a
1
, …, a
m
зависимости P
m
(x),
при которых достигается минимум суммы квадратов отклонений
этой функции от табличных значений y
i
, т.е.
2
1
( ( )
)
min
n
m
i
i
i
S
P x
y
или
2
2
0
1
2
1
...
min.
n
m
i
i
m
i
i
i
S
a
a x
a x
a x
y
(9)
Минимум функции будет найден, если приравнять к нулю
частные производные от S по a
0
, a
1
, …, a
m
, при этом получается
система m+1 уравнений

130
2
0
1
2
1
0
2
0
1
2
1
1
2
2
0
1
2
1
2
2
(
...
) 1 0,
2
(
...
)
0,
2
(
...
)
0,
.....................................................
n
m
i
i
m
i
i
i
n
m
i
i
m
i
i
i
i
n
m
i
i
m
i
i
i
i
S
a
a x
a x
a
x
y
a
S
a
a x
a x
a
x
y
x
a
S
a
a x
a x
a
x
y
x
a
2
0
1
2
1
...............................
2
(
...
)
0.
n
m
m
i
i
m
i
i
i
i
m
S
a
a x
a x
a
x
y
x
a
(10)
Сократив каждое уравнение системы (10) на 2, раскрыв
скобки и сгруппировав суммы, получаем следующую систему
(для краткости записи вместо
1
n
i
используем
) :
2
0
1
2
2
3
1
0
1
2
2
3
4
2
2
0
1
2
...
,
...
,
...
,
.....................................................................................
m
i
i
m
i
i
m
i
i
i
m
i
i
i
m
i
i
i
m
i
i
i
a n
a
x
a
x
a
x
y
a
x
a
x
a
x
a
x
y x
a
x
a
x
a
x
a
x
y x
1
2
2
0
1
2
.......
...
.
m
m
m
m
m
i
i
i
m
i
i
i
a
x
a
x
a
x
a
x
y x
(11)
Система уравнений (11) относительно неизвестных a
0
, a
1
,
…, a
m
является линейной, поэтому может быть решена, напри-
мер, методом Гаусса. Полученные в результате значения a
0
, a
1
,
…, a
m
подставляют в (8), что позволяет полностью определить
аппроксимирующую функцию.
Блок-схема алгоритма аппроксимации табличных зависимо-
стей многочленом степени m для n точек методом наименьших
квадратов приведена на рис. 29. В связи с тем, что матрица коэф-
фициентов системы уравнений a
ij
содержит попарно повторяющие-
ся элементы, для ее формирования используется вспомогательный