Файл: Контрольная работа Математические методы теории сетей связи.pdf
ВУЗ: Санкт-Петербургский государственный университет телекоммуникаций им. проф. М. А. Бонч-Бруевича
Категория: Методичка
Дисциплина: Сети связи
Добавлен: 25.10.2018
Просмотров: 4252
Скачиваний: 34
Код (10,5) с порождающим многочленом g(x)=1+x
2
+x
5
является укоро-
ченным кодом Хемминга, так как многочлен 1+х
2
+х
5
– примитивный мно-
гочлен, принадлежащий показателю 31.
В таблице неприводимых многочленов он указан условной записью 1 45 Е.
Наиболее простое решение задачи состоит в построении генератора
элементов поля GF(2
5
) и нахождении десяти первых значений степеней
примитивного корня. Их двоичное представление даст столбцы провероч-
ной матрицы в канонической форме:
H
(10,5)
=[α
0
, α
1
, α
2
, α
3
, α
4
, α
5
, α
6
, α
7
, α
8
, α
9
], где α
i
– элемент поля GF(2
5
).
Затем по проверочной матрице и известным правилам найдем порож-
дающую матрицу. Она также получится в канонической форме.
Генератор элементов поля GF(2
5
), построенный на основе примитив-
ного многочлена 1+х
2
+х
5
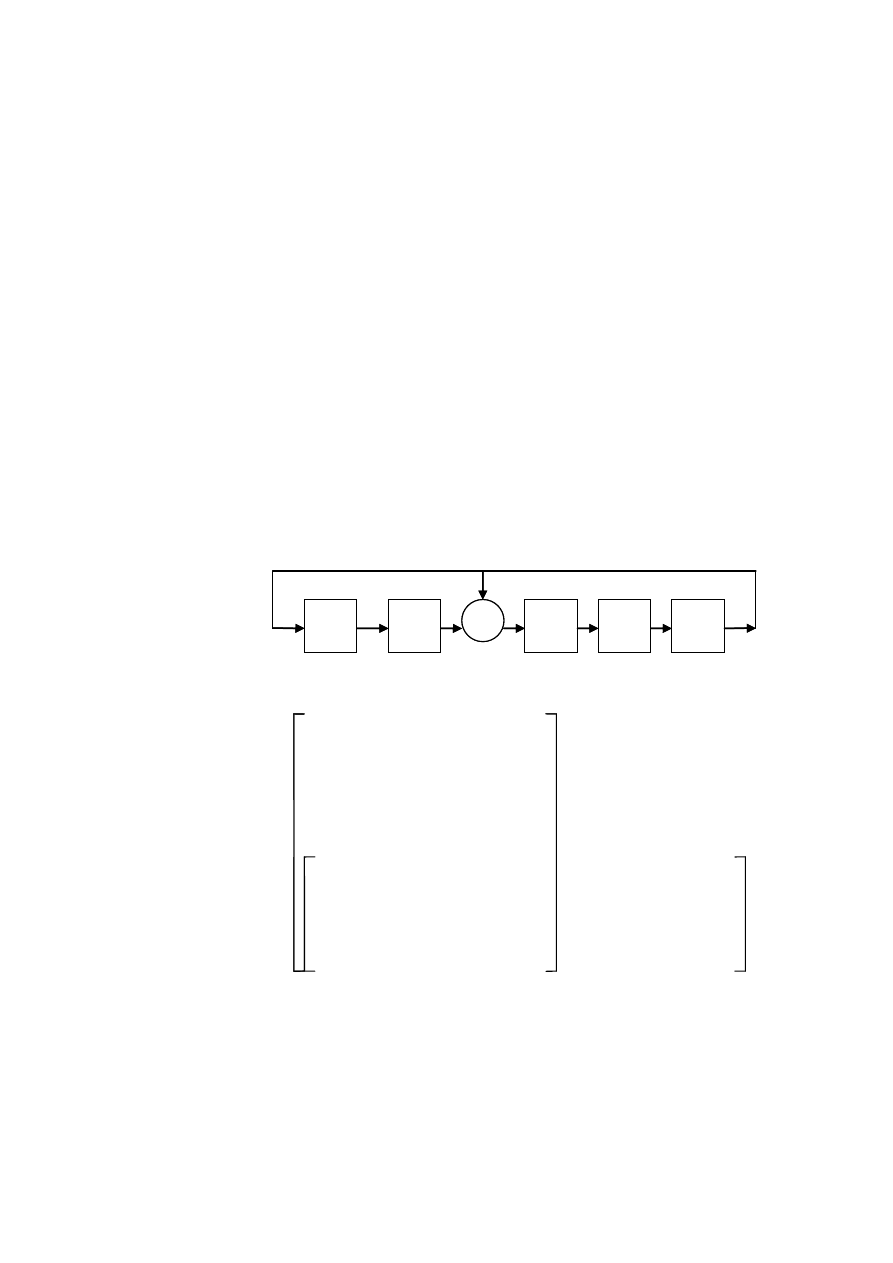
, содержимое ячеек памяти на 10 тактах работы и
матрицы, характеризующие код, представлены на рис. 1.
5.4. Построить декодер Меггита для циклического кода (7,5) над полем
GF(2
3
) c порождающим многочленом g(x)=х
2
+α
4
х+α
3
. Код гарантийно
справляет однократные ошибки.
Значения элементов поля GF(2
3
):
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
1 0 1 0 0 1 0 0 0 0
0 1 0 1 0 0 1 0 0 0
0 0 1 0 1 0 0 1 0 0
1 0 1 1 0 0 0 0 1 0
0 1 0 1 1 0 0 0 0 1
Рис. 1
+
H
T
(10,5)
=
G
(10,5)
=
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
1 0 1 0 0 1 0 0 0 0
0 1 0 1 0 0 1 0 0 0
0 0 1 0 1 0 0 1 0 0
1 0 1 1 0 0 0 0 1 0
0 1 0 1 1 0 0 0 0 1
Рис.1
+
H
T
(10,5)
=
G
(10,5)
=

0 = 000
α
0
= 1 =100
α
1
= α =010
α
2
= α
2
= 001
α
3
=1+α =110
α
4
= α+α
2
= 011
α
5
=1+α+α
2
=111
α
6
=1 +α
2
=101
α
7
= 1 =100
Решить самостоятельно.
6.
Быстрое декодирование кодов БЧХ
Коды Рида–Соломона. Определение, построение порождающего мно-
гочлена для кодов с требуемыми свойствами.
Ключевое уравнение. Алгоритм
Форни.
Методы решения ключевого уравнения по алгоритмам Берлекемпа–
Месси
и
Евклида.
Решение задач по исправлению ошибок на основе алгоритмов Берле-
кемпа–Месси и Евклида.
Литература: [7,8].
Цель. Изучить методы быстрого декодирования кодов БЧХ примени-
тельно к кодам Рида–Соломона, приобрести навыки использования мето-
дов быстрого декодирования для исправления ошибок в декодере и нахож-
дения избыточных элементов в кодере.
Контрольные вопросы
6.1. Вычислить порождающий многочлен для кода Рида–Соломона (7,5).
6.2. Методом быстрого декодирования закодировать кодом Рида–
Соломона (7,5) свой порядковый номер в журнале группы.
6.3. Для кода Рида–Соломона (7,5) построить кодер на основе регистра
сдвига с обратными связями и закодировать комбинацию из предыдущей
задачи. Сравнить результаты кодирования.
6.4. С помощью кодера предыдущей задачи построить порождающую
и проверочную матрицы кода Рида–Соломона (7,5) в канонической форме.
6.5. Вычислить порождающий многочлен для кода Рида–Соломона (7,3).
Примеры решения задач и дополнительные задачи
6.6. Построить код Рида–Соломона (7,4) над полем GF(2
3
).
Решение
Находим порождающий многочлен по теореме Безу:
g(x) = (x+α)(x+α
2
)(х+α
3
) = (x
2
+α
2
x+αx+α
3
)(x+α
3
) =
=х
3
+α
2
х
2
+αх
2
+α
3
х+α
3
х
2
+α
5
х+ α
4
х +α
6
=
= х
3
+(α+α
2
+α
3
)х+(α
3
+α
4
+α
5
)х +α
6
=х
3
+α
6
х
2
+αх+α
6
и по формуле Виета:
g
3
=1, g
2
= α+α
2
+α
3
= α
6
, g
1
= αα
2
+ αα
3
+α
2
α
3
=α
3
+α
4
+α
5
=α, g
0
=αα
2
α
3
=α
6
.
Итак, g(x) = х
3
+α
6
х
2
+αх+α
6
.
Для построения порождающей и проверочной матриц воспользуемся
приемом, примененным в п. 5.3. Строим генератор элементов GF(2
3
) по ви-
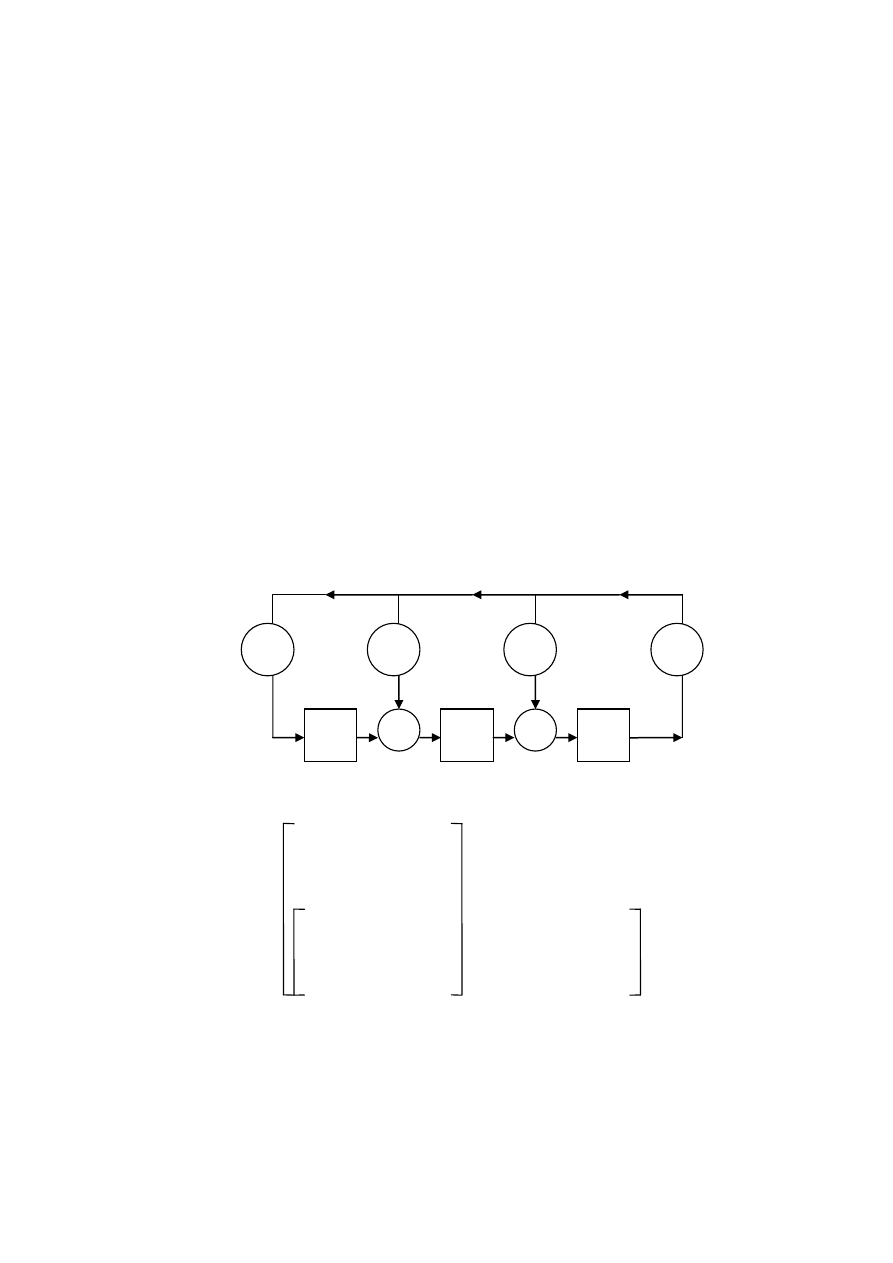
ду g(x) (рис. 2). Записав в крайнюю слева ячейку памяти «1», выполним 7
сдвигов до получения в ячейках регистра исходной последовательности
1 0 0. Содержимое ячеек памяти регистра на первых 7 тактах работы схе-
мы соответствует строкам транспонированной проверочной матрицы ко-
да. Последние четыре строки данной матрицы соответствуют столбцам
порождающей матрицы этого кода, расположенных на местах избыточ-
ных элементов в канонической форме. Приписав к ним справа единичную
матрицу размером 4×4, получаем всю порождающую матрицу кода (7,4) в
канонической форме.
Рис. 2
1 0 0
0 1 0
0 0 1
α
6
α
1
α
6
1 0 0 0
α
5
α
2
α
6
0 1 0 0
α
5
α
4
α
3
0 0 1 0
α
2
α
0
α
1
0 0 0 1
1 0 0
α
0
α
1
α
6
α
6
+
+
H
T
(7,4)
=
G
(7,4)
=

ПРИЛОЖЕНИЕ
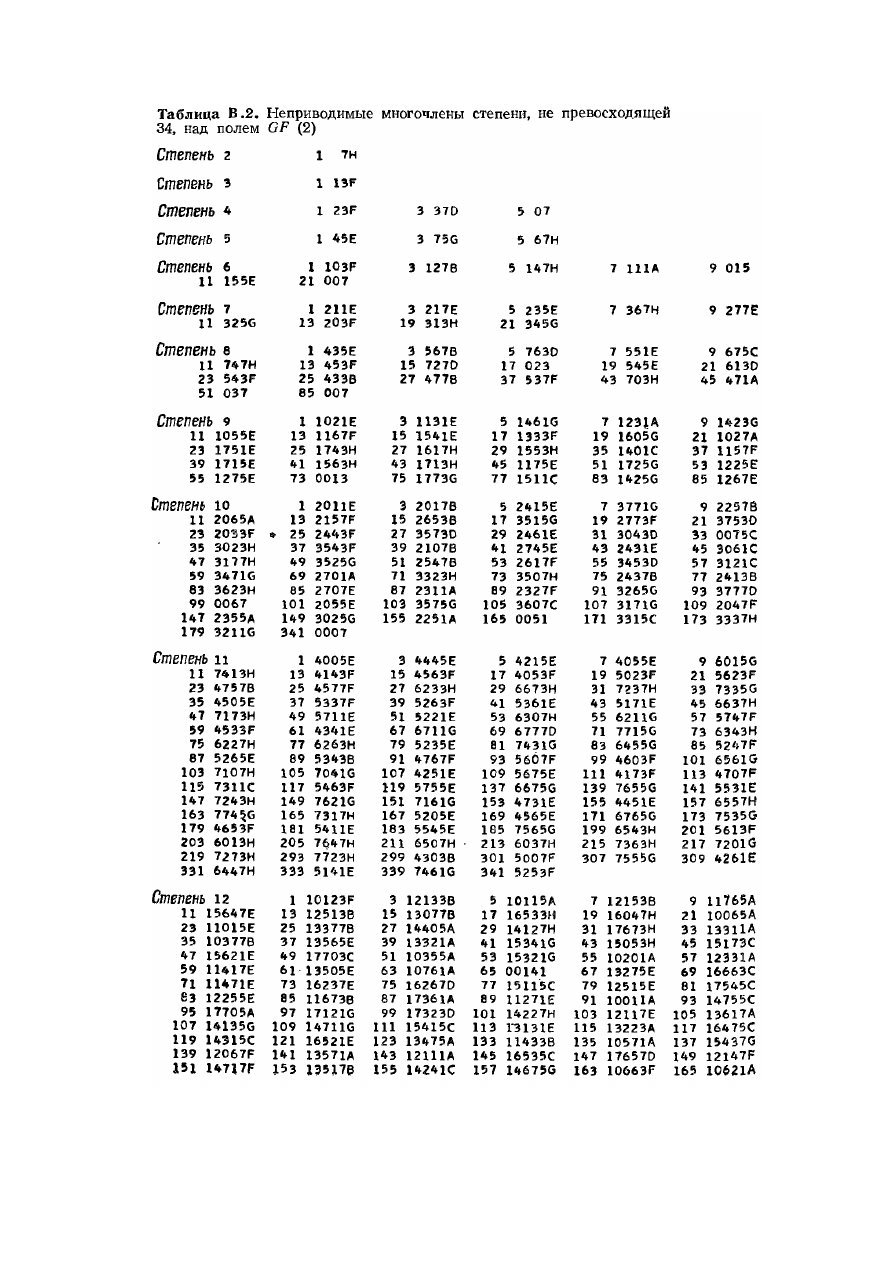
(фрагмент табл.В.2. из[1])