Добавлен: 26.10.2018
Просмотров: 641
Скачиваний: 4

КОНТРОЛЬНАЯ РАБОТА №2
РАЗДЕЛ 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПРЕМЕННОЙ
ВАРИАНТ 1
1. Найдите производную функции
x
x
x
f
2
3
по определению.
2. Напишите уравнения касательной и нормали к графику функции
3
8
2
2
x
x
y
в точке
1
0
x
.
Постройте график функции, касательную и нормаль к ней.
3. Для точки, движущейся прямолинейно по закону
3
5
2
3
2
3
t
t
t
t
s
, найдите скорость и уско-
рение, в момент еѐ остановки. (Время t измеряется в секундах, перемещение s - в метрах).
4. Найдите производную
x
y
, если: а)
x
x
x
x
x
y
x
4
2
2
cos
1
2
3
5
; б)
0
4
4
2
2
y
xy
x
;
в)
t
a
x
2
cos
,
t
a
y
2
sin
.
5. Найдите производную сложной функции
2
4
1
ln
2
x
y
.
6. Найдите производную и дифференциал функции
x
x
y
, используя логарифмическое диффе-
ренцирование.
7. Найдите
вторую
производную
и
дифференциал
второго
порядка
функции
3
2
arcsin
1
x
x
y
.
8. Найдите значение выражения
5
1
,
1
, заменяя приращение функции еѐ дифференциалом.
9. Вычислите пределы а)
x
x
x
ctg
arcsin
lim
0
, б)
x
x
x
arccos
2
lim
0
, используя правило Лопиталя.
10. Исследуйте свойства функции
x
xe
y
1
и постройте еѐ график.
11. Найдите наибольшее и наименьшее значения функции
x
x
y
3
2
на отрезке
3
;
1
.
12. Решите задачу. Как разрезать отрезок длиной 10 см на две части так, чтобы, взяв их за катеты,
получить треугольник с наименьшей гипотенузой?
ВАРИАНТ 2
1. Найдите производную функции
2
3
x
x
x
f
по определению.
2. Напишите уравнения касательной и нормали к графику функции
3
4
2
x
x
y
в точке
0
0
x
.
Постройте график функции, касательную и нормаль к ней.
3. Для точки, движущейся прямолинейно по закону
5
6
2
3
2
3
t
t
t
t
s
, найдите скорость и уско-
рение, в момент еѐ остановки. (Время t измеряется в секундах, перемещение s - в метрах).
4. Найдите производную
x
y
, если а)
x
x
x
x
y
x
2
3
2
log
3
1
1
; б)
x
y
x
sin
; в)
2
1 t
x
,
3
t
t
y
.
5. Найдите производную сложной функции
x
x
y
7
1
2
2
.
6. Найдите производную и дифференциал функции
x
x
y
1
, используя логарифмическое диффе-
ренцирование.
7. Найдите
вторую
производную
и
дифференциал
второго
порядка
функции
2
3
arccos
2
x
x
y
.
8. Найдите значение выражения
1
,
4
, заменяя приращение функции еѐ дифференциалом.
9. Вычислите пределы а)
1
ln
ln
lim
1
x
x
x
, б)
x
x
x
x
1
3
lim
, используя правило Лопиталя.
10. Исследуйте свойства функции
x
x
y
ln
2
и постройте еѐ график.
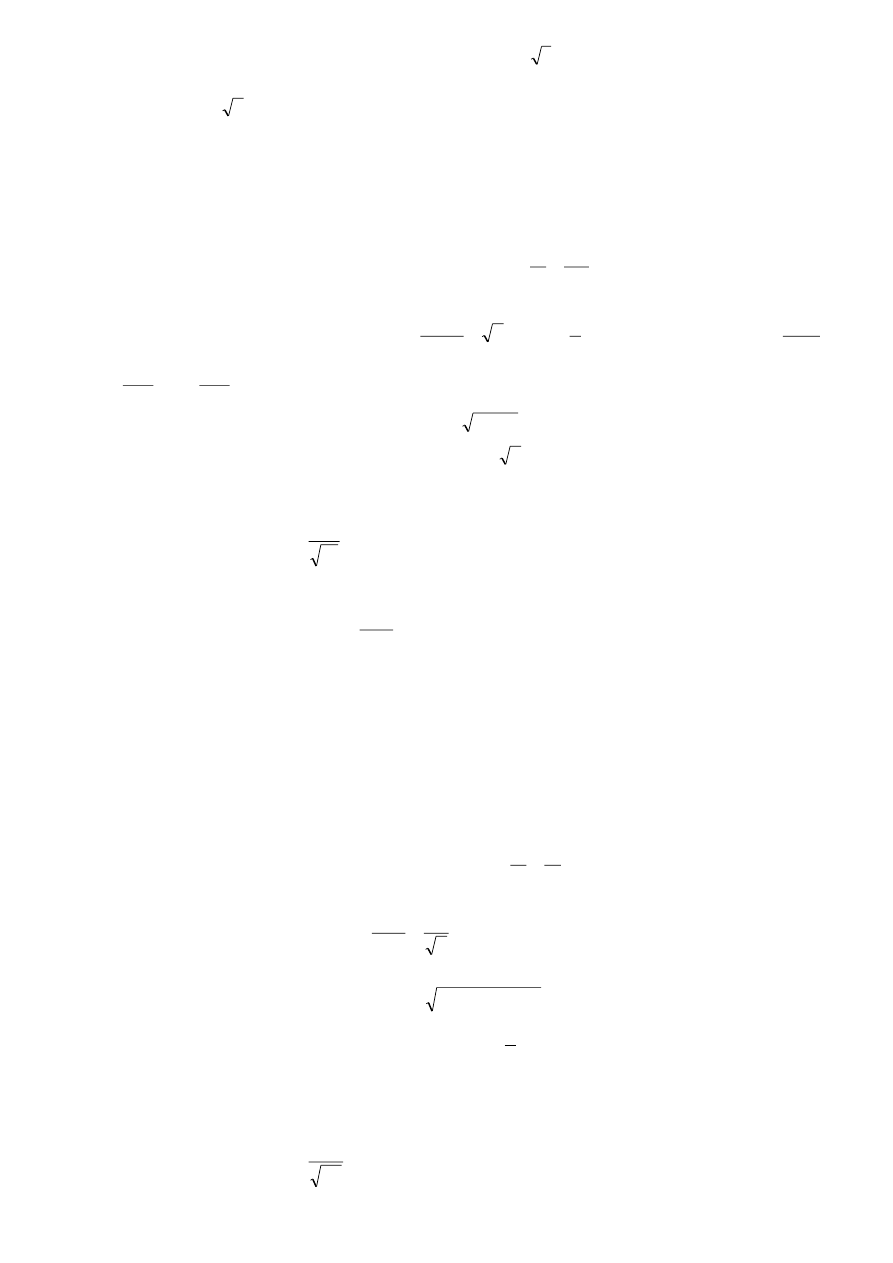
2
11. Найдите наибольшее и наименьшее значения функции
x
x
y
2
sin
3
на отрезке
;
0
.
12. Решите задачу. При каком значении высоты прямоугольная трапеция с острым углом
45
и пе-
риметром
2
1
4
P
имеет наибольшую площадь?
ВАРИАНТ 3
1. Найдите производную функции
2
3
x
x
f
по определению.
2. Напишите уравнения касательной и нормали к графику функции
4
2
2
x
x
y
в точке
1
0
x
.
Постройте график функции, касательную и нормаль к ней.
3. Для точки, движущейся прямолинейно по закону
2
10
2
3
3
2
3
t
t
t
t
s
, найдите скорость и
ускорение, в момент еѐ остановки. (Время t измеряется в секундах, перемещение s - в метрах).
4. Найдите производную
x
y
, если а)
2
1
ctg
1
2
ln
3
x
x
x
x
x
y
; б)
x
x
y
2
1
2
log
3
;
в)
t
t
x
1
,
t
t
y
1
.
5. Найдите производную сложной функции
2
5
7
log
2
x
e
x
y
.
6. Найдите производную и дифференциал функции
x
x
y
, используя логарифмическое диффе-
ренцирование.
7. Найдите вторую производную и дифференциал второго порядка функции
1
2
arctg
4
x
x
y
.
8. Найдите значение выражения
5
1
,
1
1 , заменяя приращение функции еѐ дифференциалом.
9. Вычислите пределы а)
x
x
x
tg
ln
lim
0
, б)
x
x
x
sin
0
ctg
lim
, используя правило Лопиталя.
10. Исследуйте свойства функции
1
ln
x
x
y
и постройте еѐ график.
11. Найдите наибольшее и наименьшее значения функции
3
2
2
4
x
x
y
на отрезке
2
;
3
.
12. Решите задачу. Забором длиной 80 м нужно огородить прямоугольную площадку наибольшей
площади. Найдите размеры этой площадки.
ВАРИАНТ 4
1. Найдите производную функции
2
3
4x
x
x
f
по определению.
2. Напишите уравнения касательной и нормали к графику функции
10
8
2
2
x
x
y
в точке
1
0
x
.
Постройте график функции, касательную и нормаль к ней.
3. Для точки, движущейся прямолинейно по закону
7
3
2
3
2
3
t
t
t
t
s
, найдите скорость и уско-
рение, в момент еѐ остановки. (Время t измеряется в секундах, перемещение s - в метрах).
4. Найдите производную
x
y
, если а)
x
x
x
x
y
x
5
,
0
3
log
4
3
2
3
1
; б)
x
xy
4
log
4
; в)
1
ln
2
t
x
,
t
t
y
arctg
.
5. Найдите производную сложной функции
x
x
y
ln
2
sin
3
.
6. Найдите производную и дифференциал функции
x
x
y
1
, используя логарифмическое диффе-
ренцирование.
7. Найдите
вторую
производную
и
дифференциал
второго
порядка
функции
2
3
arccos
1
x
x
y
.
8. Найдите значение выражения
1
,
4
1
, заменяя приращение функции еѐ дифференциалом.

3
9. Вычислите пределы а)
x
x
e
x
lim
, б)
4
1
2
sin
lim
4
x
x
x
, используя правило Лопиталя.
10. Исследуйте свойства функции
4
2
3
x
x
y
и постройте еѐ график.
11. Найдите наибольшее и наименьшее значения функции
x
x
y
2
на отрезке
0
;
4
.
12. Решите задачу. Боковые стороны и меньшее основание трапеции равны 10 см. Определите боль-
шее основание так, чтобы ее площадь была наибольшей.
ВАРИАНТ 5
1. Найдите производную функции
x
x
x
f
3
3
по определению.
2. Напишите уравнения касательной и нормали к графику функции
7
6
2
x
x
y
в точке
1
0
x
.
Постройте график функции, касательную и нормаль к ней.
3. Для точки, движущейся прямолинейно по закону
1
4
2
3
3
2
3
t
t
t
t
s
, найдите скорость и уско-
рение, в момент еѐ остановки. (Время t измеряется в секундах, перемещение s - в метрах).
4. Найдите
производную
x
y
,
если
а)
x
x
x
x
y
x
ln
arccos
3
1
2
3
;
б)
0
4
2
2
yx
y
;
в)
t
t
x
sin
1
,
t
t
y
cos
.
5. Найдите производную сложной функции
x
x
y
ln
1
sin
2
.
6. Найдите производную и дифференциал функции
x
x
y
, используя логарифмическое дифферен-
цирование.
7. Найдите вторую производную и дифференциал второго порядка функции
4
5
arcsin
3
x
x
y
.
8. Найдите значение выражения
5
1
,
32
, заменяя приращение функции еѐ дифференциалом.
9. Вычислите пределы а)
1
ln
1
lim
1
x
x
x
, б)
x
x
x
1
arccos
2
lim
0
, используя правило Лопиталя.
10. Исследуйте свойства функции
2
3
2
x
x
y
и постройте еѐ график.
11. Найдите наибольшее и наименьшее значения функции
x
x
y
2
2
на отрезке
16
;
0
.
12. Решите задачу. Заготовка объѐмом 72 дм
3
имеет форму прямоугольного параллелепипеда с от-
ношением сторон основания 1:2. При каких размерах площадь полной поверхности заготовки бу-
дет наибольшей?
ВАРИАНТ 6
1. Найдите производную функции
2
3
5x
x
x
f
по определению.
2. Напишите уравнения касательной и нормали к графику функции
3
4
2
x
x
y
в точке
4
0
x
. Постройте график функции, касательную и нормаль к ней.
3. Для точки, движущейся прямолинейно по закону
8
40
2
3
3
2
3
t
t
t
t
s
, найдите скорость и
ускорение, в момент еѐ остановки. (Время t измеряется в секундах, перемещение s - в метрах).
4. Найдите производную
x
y
, если а)
2
3
3
2
5
3x
tg
5
1
ln
1
2
x
x
x
x
y
; б)
x
y
x
4
2
cos
;
в)
t
e
x
t
sin
,
t
e
y
t
cos
.
5. Найдите производную сложной функции
x
x
y
4
7
arcsin
2
.
6. Найдите производную и дифференциал функции
x
x
y
1
2
, используя логарифмическое диффе-
ренцирование.

4
7. Найдите
вторую
производную
и
дифференциал
второго
порядка
функции
2
7
arcsin
2
x
x
y
.
8. Найдите значение выражения
1
,
16 , заменяя приращение функции еѐ дифференциалом.
9. Вычислите пределы а)
x
x
x
1
2
tg
lim
1
, б)
x
x
x
1
3
lim
, используя правило Лопиталя.
10. Исследуйте свойства функции
3
3
1 x
y
и постройте еѐ график.
11. Найдите наибольшее и наименьшее значения функции
x
x
y
cos
2
на отрезке
;
.
12. Решите задачу. Определите размеры открытого бассейна с квадратным дном объемом 32 м
3
так,
чтобы на облицовку его стен и дна пошло наименьшее количество материала.
ВАРИАНТ 7
1. Найдите производную функции
x
x
x
f
4
3
по определению.
2. Напишите уравнения касательной и нормали к графику функции
17
8
2
x
x
y
в точке
3
0
x
. Постройте график функции, касательную и нормаль к ней.
3. Для точки, движущейся прямолинейно по закону
12
6
2
3
2
3
t
t
t
t
s
, найдите скорость и уско-
рение, в момент еѐ остановки. (Время t измеряется в секундах, перемещение s - в метрах).
4. Найдите
производную
x
y
, если а)
x
x
x
x
x
y
x
ln
5
3
1
2
1
arcsin
3
2
2
4
; б)
y
y
x
2
5
;
в)
t
t
x
2
2
,
t
t
y
3
.
5. Найдите производную сложной функции
2
2
1
5
3
tg
log
x
x
y
.
6. Найдите производную и дифференциал функции
x
x
y
ctg
tg
, используя логарифмическое диффе-
ренцирование.
7. Найдите вторую производную и дифференциал второго порядка функции
1
2
arctg
3
x
x
y
.
8. Найдите значение выражения
5
1
,
32
1
, заменяя приращение функции еѐ дифференциалом.
9. Вычислите пределы а)
x
x
x
ctg
lim
0
, б)
x
x
x
1
1
lim
, используя правило Лопиталя.
10. Исследуйте свойства функции
x
x
y
ln
2
и постройте еѐ график.
11. Найдите наибольшее и наименьшее значения функции
x
x
y
9
на отрезке
9
;
2
1
.
12. Решите задачу. Число 6 представьте в виде суммы двух слагаемых так, чтобы сумма их кубов
была наибольшей.
ВАРИАНТ 8
1. Найдите производную функции
2
3
x
x
x
f
по определению.
2. Напишите уравнения касательной и нормали к графику функции
13
8
2
x
x
y
в точке
2
0
x
.
Постройте график функции, касательную и нормаль к ней.
3. Для точки, движущейся прямолинейно по закону
3
6
2
5
3
2
3
t
t
t
t
s
, найдите скорость и уско-
рение, в момент еѐ остановки. (Время t измеряется в секундах, перемещение s - в метрах).
4. Найдите производную
x
y
, если а)
x
x
x
x
x
y
x
2
2
1
log
2
3
4
2
cos
1
7
; б)
1
9
6
2
2
y
xy
x
;
в)
t
t
x
2
cos
cos
2
,
t
t
y
2
sin
sin
2
.
5. Найдите производную сложной функции
x
y
x
x
2
5
sin
3
2
.

5
6. Найдите производную и дифференциал функции
2
x
x
y
, используя логарифмическое дифферен-
цирование.
7. Найдите
вторую
производную
и
дифференциал
второго
порядка
функции
1
3
arcctg
4
x
x
y
.
8. Найдите значение выражения
1
,
16
1
, заменяя приращение функции еѐ дифференциалом.
9. Вычислите пределы а)
x
c
x
x
tg
cos
1
lim
0
, б)
ctgx
x
x
cos
lim
0
, используя правило Лопиталя.
10. Исследуйте свойства функции
x
x
y
ln
и постройте еѐ график.
11. Найдите наибольшее и наименьшее значения функции
x
e
x
y
2
на отрезке
3
;
1
.
12. Решите задачу. Из прямоугольно листа картона размером 24
15 м
2
, вырезая квадраты из четырех
углов, требуется изготовить открытую коробку наибольшего объѐма. Каковы размеры этой ко-
робки?
ВАРИАНТ 9
1. Найдите производную функции
x
x
x
f
6
3
по определению.
2. Напишите уравнения касательной и нормали к графику функции
10
6
2
x
x
y
в точке
4
0
x
.
Постройте график функции, касательную и нормаль к ней.
3. Для точки, движущейся прямолинейно по закону
2
8
3
2
3
t
t
t
t
s
, найдите скорость и уско-
рение, в момент еѐ остановки. (Время t измеряется в секундах, перемещение s - в метрах).
4. Найдите производную
x
y
, если а)
x
x
x
x
x
y
x
ln
3
arctg
2
1
2
1
5
3
2
; б)
x
y
x
3
2
ln
;
в)
t
x
cos
,
t
t
y
sin
2
.
5. Найдите производную сложной функции
3
2
2
sin
x
x
y
.
6. Найдите производную и дифференциал функции
2
x
x
y
, используя логарифмическое диффе-
ренцирование.
7. Найдите
вторую
производную
и
дифференциал
второго
порядка
функции
5
4
arccos
2
x
x
y
.
8. Найдите значение выражения
5
1
,
243
, заменяя приращение функции еѐ дифференциалом.
9. Вычислите пределы а)
x
x
e
x
1
0
arcsin
lim
, б)
2
cos
1
lim
1
x
x
x
, используя правило Лопиталя.
10. Исследуйте свойства функции
x
e
y
x
и постройте еѐ график.
11. Найдите наибольшее и наименьшее значения функции
2
1
2
x
x
y
на отрезке
2
5
;
0
.
12. Решите задачу. Из круглого бревна с радиусом сечения 20см требуется вырезать брус прямо-
угольного сечения так, чтобы получилось наименьшее количество отходов. Определите размеры
прямоугольного сечения бруса.
ВАРИАНТ 10
1. Найдите производную функции
2
3
2x
x
x
f
по определению.
2. Напишите уравнения касательной и нормали к графику функции
2
2
2
x
x
y
в точке
2
0
x
.
Постройте график функции, касательную и нормаль к ней.
3. Для точки, движущейся прямолинейно по закону
1
20
2
3
2
3
t
t
t
t
s
, найдите скорость и уско-