ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса
Категория: Методичка
Дисциплина: Системы искусственного интеллекта
Добавлен: 29.10.2018
Просмотров: 323
Скачиваний: 9
ЛАБОРАТОРНАЯ РАБОТА №4.
ТЕМА: НЕЧЕТКИЕ МНОЖЕСТВА В ПИЩЕВОЙ ПРОМЫШЛЕННОСТИ.
Согласно техническим условиям молочная колбаса высшего сорта должна содержать
Жира: 13,5 -15,5 %, Белков: 14,6 – 15,4%.
Нескольким дегустаторам было поручено определить наиболее предпочтительное вкусовое содержание этих составляющих в заданных т.у. пределах. При этом от них требовалась следующая четырехбалльная оценка:
Вкусно – 1,
Скорее вкусно, чем невкусно – 0.8,
Скорее невкусно, чем вкусно – 0.3,
Невкусно – 0.
После статистической обработки (определялось среднее арифметическое их ответов) были получены матрицы оценок, приведенные на рис.1
Рис.1. матрицы оценок содержания жира и белков в молочной колбасе.
Здесь в первой строке – процентное содержание жира и белков, а во второй – их оценка.
Необходимо выбрать аналитическую зависимость для обеих функций принадлежности. Рассмотрение первой матрицы показывает, что она хорошо аппроксимируется нормальным законом распределения (см. рис.2).Поэтому выбираем для нее аналитическую зависимость
, (1)
а за начальные приближения для коэффициентов А1 и В1 примем, соответственно, среднее арифметическое и величину, обратную дисперсии. Так как маткад требует вычисления среднего арифметического и дисперсии от вектора - столбца, введем вспомогательный вектор –строку v1, которую потом транспонируем.
. (2)
З
атем
вычисляем начальные приближения:
Здесь т – индекс транспонирования.
Уточненные значения коэффициентов А1 и В1 будем искать методом наименьших квадратов, используя функцию Minerr (minimum error – минимальная ошибка). Как говорилось ранее, эта функция ищет в блоке решений вектор значений, приводящей к минимальной ошибке в системе уравнений. Записав ключевое слово Given, открывающее блок решений, записываем и приравниваем нулю (жирным знаком = из панели «логические») сумму квадратов. Применив функцию Minerr, вычисляем уточненные значения искомых коэффициентов.
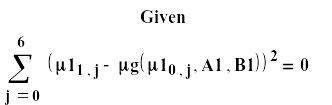(4)
(5)
График полученной функции принадлежности на рис.2 показывает, что она хорошо аппроксимирует экспериментальные точки.
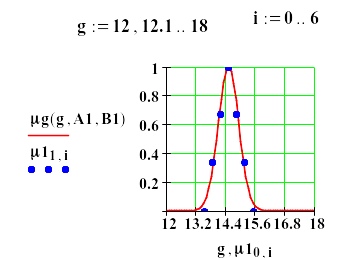
Рис.2 . График аналитического выражения для функции принадлежности жира.
Рассмотрим теперь вторую матрицу рис.1. Мы видим, что левая часть ее второй строки является константой, а правая практически повторяет правую часть второй строки первой матрицы. По- видимому, при аппроксимации функции принадлежности аналитическим выражением логично задаться для левой части единицей, а для правой – нормальным законом распределения. Для определения параметров нормального закона составим симметричную вспомогательную матрицу μ20, приведенную на рис.3.
Рис. 3. Вспомогательная матрица.
Повторяя все действия , проведенные для матрицы μ1, определим параметры нормального закона распределения для
матрицы μ20:
Зададимся законом распределения
, (6)
сформируем вспомогательный вектор v2 и начальные приближения коэффициентов А20 и В20:,
(7)
Используя функцию Minerr, уточним эти значения:
Результаты показывают, что уточнение в данном случае ничего не дало: уточненные коэффициенты совпадают с первоначально заданными.
Построим график полученной кривой (см. рис.4). Из рассмотрения точек и кривой видно, что аппроксимация проведена удовлетворительно.
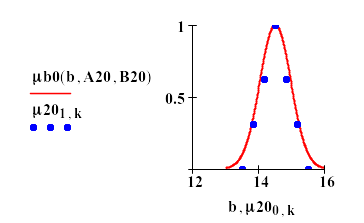
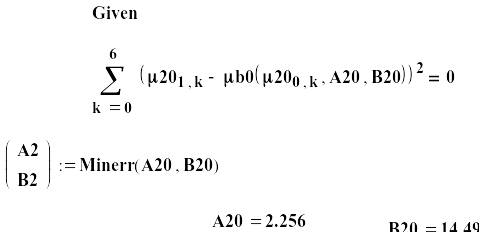
Рис.4. Аппроксимация вспомогательной матрицы.
Для аппроксимации матрицы μ2 введем новое обозначение для функции принадлежности и используем условный оператор if:
(10)
График полученной функции принадлежности и аппроксимируемые точки приведены на рис.5.
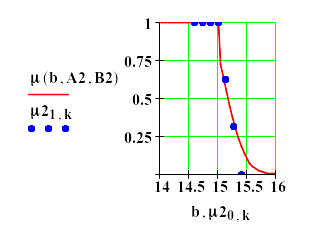
Рис.5 . График аналитического выражения функции принадлежности для белков.
Для определения оптимального содержания и жиров и белков в колбасе нам нужно найти пересечение обеих функций принадлежности и определить максимум новой функции принадлежности.
П
ересечение
ищем в виде функции двух переменных
μgb (g,b),
используя функцию маткада min.
(11)
Трехмерный график новой функции принадлежности представлен на рис. 6.
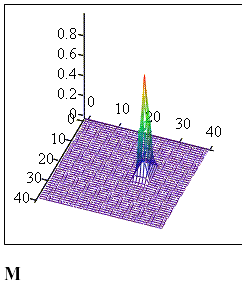
Рис.6. График пересечения функций принадлежности жира и белка.
Для нахождения максимума этой функции, т.е. оптимального с точки зрения экспертов содержания жира и белков в молочной колбасе, составим небольшую программу, приведенную на рис.7.
П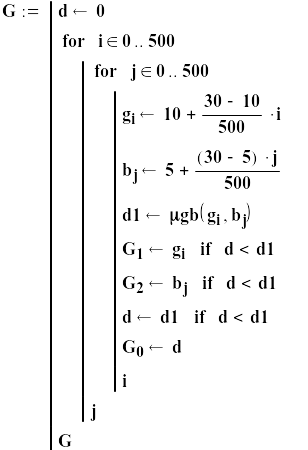
рограмма
совершенно аналогична программам
вычисления максимума функции двух
переменных, составленных на любом из
алгоритмических языков высокого уровня.
Следует только отметить, что большое
количество узлов (500х500) выбрано из за
большой величины градиента функции в
области максимума, что видно на рис.7.
В
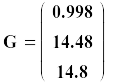результате выполнения программы получен
вектор ответов
Рис.7. Программа вычисления максимума пересечения функций принадлежности жира и белка
Здесь первый элемент – максимальное значение функции, второй – оптимальное с точки зрения экспертов содержание жира, а третий – оптимальное содержание белков в молочной колбасе (в процентах).