Связь между общей, факторной и остаточной суммами

Покажем, что

Для упрощения вывода ограничимся двумя уровнями и двумя испытаниями на каждом уровне и двумя испытаниями на каждом уровне и двумя испытаниями на каждом уровне Результаты испытаний представим в виде таблицы 2.

Таблица 2

Номер испытания	Уровни фактора
l
1 2

Тогда

Вычтем и прибавим к каждому наблюдаемому значению на первом уровне групповую среднюю а на втором – . Выполнив возведение в квадрат и учитывая, что сумма всех удвоенных произведений равна нулю (рекомендуем читателю убедиться в этом самостоятельно), получим

=

Итак,

Следствие. Из полученного равенства вытекает важное следствие:

Отсюда видно, что нет надобности непосредственно вычислять остаточную сумму: достаточно найти общую и факторную суммы, а затем их разность.

2.4.Общая, факторная и остаточная дисперсии

Разделив суммы квадратов отклонений на соответствующее число степеней свободы, получим общую, факторную и остаточную дисперсии:

где - число уровней фактора; - число наблюдений на каждом уровне; – число степеней свободы факторной дисперсии; – число степеней свободы остаточной дисперсии.

Если нулевая гипотеза о равенстве средних справедлива, то все эти дисперсии являются несмещенными оценками генеральной дисперсии. Например, учитывая, что объем выборки , заключаем, что

– исправленная выборочная дисперсия, которая, как известно, является несмещенной оценкой генеральной дисперсии.

Замечание. Число степеней свободы остаточной дисперсии равно разности между числами степеней свободы общей и факторной дисперсий. Действительно,

.

2.5.Сравнение нескольких средних методом дисперсионного анализа

Вернемся к задаче, поставленной в п. 2.1: проверить при заданном уровне значимости нулевую гипотезу: о равенстве нескольких средних нормальных совокупностей с неизвестными, но одинаковыми диспериями. Покажем, что решение этой задачи сводится к сравнению факторной и остаточной дисперсий по критерию Фишера – Снедекора.

1. Пусть нулевая гипотеза о равенстве нескольких средних (далее будем называть их групповыми) правильна. В этом случае факторная и остаточная дисперсии являются несмещенными оценками неизвестной генеральной дисперсии (см. п. 2.4) и, следовательно, различаются незначимо. Если сравнить эти оценки по критерию , то очевидно, критерий укажет, что нулевую гипотезу о равенстве факторной и остаточной дисперсий следует принять.

Таким образом, если гипотеза о равенстве групповых средних правильна, то верна и гипотеза о равенстве факторной и остаточной дисперсий.

2. Пусть нулевая гипотеза о равенстве групповых средних ложна. В этом случае с возрастанием расхождения между групповыми средними увеличивается факторная дисперсия, а вместе с ней и отношение В итоге окажется больше и, следовательно, гипотеза о равенстве дисперсий будет отвергнута.

---

Таким образом, если гипотеза о равенстве групповых средних ложна, то ложна и гипотеза о равенстве факторной и остаточной дисперсий.

Легко доказать от противного справедливость обратных утверждений: из правильности (ложности) гипотезы о дисперсиях следует правильность (ложность) гипотезы о средних.

Итак, для того чтобы проверить нулевую гипотезу о равенстве групповых средних нормальных совокупностей с одинаковыми дисперсиями, достаточно проверить по критерию нулевую гипотезу о равенстве факторной и остаточной дисперсий. В этом и состоит метод дисперсионного анализа.

Замечание 1. Если факторная дисперсия окажется меньше остаточной, то уже отсюда следует справедливость гипотезы о равенстве групповых средних и, значит, нет надобности прибегать к критерию .

Замечание 2. Если нет уверенности в справедливости предположения о равенстве дисперсий рассматриваемых p совокупностей, то это предположение следует проверить предварительно, например по критерию Кочрена.

Пример. Произведено по 4 испытания на каждом из трех уровней. Результаты испытаний приведены в таблице 3. Методом дисперсионного анализа при уровне значимости 0,05 проверить нулевую гипотезу о равенстве групповых средних.

Таблица 3

Номер испытания	Уровни фактора
i
1 2 3 4	51 52 56 57	52 54 56 58	42 44 50 52
	54	55	47

Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.

Решение. Для упрощения расчета вычтем из каждого наблюдаемого значения: Составим расчетную таблицу 4.

Таблица 4

Номер испытания	Уровни фактора						Итоговый столбец
i
1 2 3 4	–1 0 4 5	1 0 16 25	0 2 4 6	0 4 16 36	– 10 – 8 – 2 0	100 64 4 0
		42		56		168
	8		12		– 20
	64		144		400

Пользуясь таблицей и учитывая, что число уровней фактора , число испытаний на каждом уровне , найдем общую и факторную суммы квадратов отклонений (см. п. 2.2, формулы и ):

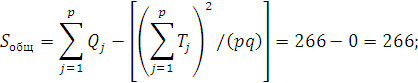
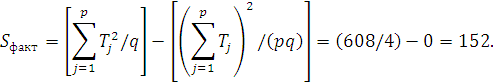
Найдем остаточную сумму квадратов отклонений:

Найдем факторную и остаточную дисперсии:

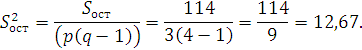
Сравним, факторную и остаточную дисперсии по критерию F, для чего найдем наблюдаемое значение критерия:

Учитывая, что число степеней свободы числителя а знаменателя и уровень значимости по таблице приложения 1 находим критическую точку:

Так как - нулевую гипотезу о равенстве групповых средних отвергаем. Другими словами, групповые средние «в целом» различаются значимо. Если требуется сравнить средние попарно, то следует воспользоваться критерием Стьюдента.

---

Замечание 3. Если наблюдаемые значения - десятичные дроби с одним знаком после запятой, то целесообразно перейти к числам , где C – примерно среднее значение чисел В итоге получим сравнительно небольшие целые числа. Хотя при этом факторная и остаточная дисперсия увеличиваются в раз, их отношение не изменится. Например, если то, приняв получим:

Аналогично поступают, если после запятой имеется знаков:

---

Смотрите также файлы

• Лекция 2. Элементы дисперсионного анализа.doc

• Лекция 1. Графический способ обработки опытных данных.doc

• Задание на контрольную работу №1.doc

• Лекция 3. Этапы проектирования.doc

• Лекция 2. Система, управление, информация.doc