Методические указания к выполнению

ИНДИВИДУАЛЬНОГО ЗАДАНИЯ по дисциплине

«ТЕОРИЯ АЛГОРИТМОВ»

(для студентов направления подготовки 09.03.02 «Информационные системы и технологии»)

---

В методических указаниях изложены теоретические основы описания синтаксиса формальных языков, методов разработки порождающих грамматик, грамматик-распознавателей и методов синтаксического анализа конструкций языков программирования. Теоретический материал иллюстрирован примерами, которые направлены на практическое применение теоретических знаний, приведены задания для выполнения работы.

Тема: Формальные языки.

Цель работы: Изучение метаязыков описания синтаксиса формальных языков, методов разработки порождающих грамматик, грамматик-распознавателей и методов синтаксического анализа конструкций языков программирования.

1. Теоретические положения

Теория формальных грамматик и языков – раздел математической лингвистики.

Возникла в 50-е годы 20 века в работах американского лингвиста Н. Хомского. Изначально занимался изучением строения естественных языков. Применяемые им методы могут быть использованы для изучения специализированных языков, в частности, алгоритмических.

По характеру используемого математического аппарата ТФЯ близка к теории алгоритмов и теории конечных автоматов.

Любой язык описывается:

1) алфавитом;

2) синтаксисом – набор правил для построения и описания форм, конструкций, предложений языка;

3) семантикой – смысл, толкование конструкций языка, правила использования синтаксиса.

Предложение – конечная последовательность слов в некотором алфавите.

Грамматика – набор правил, описания синтаксиса языка.

Описание любого формального языка осуществляется обычно на другом языке, называемом метаязыком.

Метаязык может описывать либо синтаксис формального языка (форму конструкций), либо семантику (смысл этих конструкций), либо то и другое вместе.

Для языков программирования наиболее распространенными метаязыками описания синтаксиса являются:

• нормальные формы Бэкуса или форма Бэкуса-Наура (БНФ);

• модифицированные формы Бэкуса-Наура (МБНФ);

• синтаксические диаграммы (СД).

1. Основные понятия БНФ

• Терминальный символ – символ, состоящий только из букв алфавита описываемого языка. В общем случае символом может быть одна или несколько букв, имеющие вместе определенное значение. Например, ключевое слово END.

• Нетерминальный символ – сформулированное на русском или любом другом языке понятие описываемого языка программирования.

Нетерминальные символы заключаются в угловые скобки.

Например: <программа>, <символическое имя>, <арифметическое выражение>.

Нетерминальные символы называют металингвистическими переменными, переменные метаязыка.

Специальные метасимволы

• “::=” – по определению есть или представляет собой;

• “|”– или.

Примеры

<цифра> ::= 0 | 1 | 2…| 9.

<оператор> ::= <оператор присваивания > |

<оператор цикла> | <условный оператор>

---

Для того, чтобы раскрыть понятие языка, обозначаемое нетерминальным символом, используется правила подстановки (ПП) или металингвистические формулы, являются предложениями метаязыка.

В общем случае ПП:

U::=u,

где U, u – произвольные (конечные) последовательности нетерминальных и терминальных символов.

Обычно, в языках программирования

U – один нетерминальный символ,

u – любая (в том числе и пустая) последовательность нетерминальных и терминальных символов, раскрывающая сущность (возможно не до конца) нетерминального символа, стоящего в левой части подстановки.

Пример 1.

Описание синтаксиса языка целых чисел

• <целое>::= <цифры>|<знак> <цифры>

• <цифры>::= <цифра> | <цифры><цифра>

• <знак>::= + | -

<цифра>::= 0/1/2…/9.

Пример 2.

Грамматика символического имени

<символическое имя>::= <буква> |

<символическое имя> <буква-цифра>

<буква-цифра>::= < буква> | < цифра>

• <буква>::= А | …| z

• <цифра>::=0|1| … | 9.

Во многих случаях для сокращения записи и повышения наглядности описания синтаксиса используют так называемую модифицированную БНФ.

Модификация заключается в добавлении новых символов метаязыка.

Наиболее часто применяют квадратные и фигурные скобки.

Часть предложения, заключенная в квадратные скобки может либо присутствовать, либо отсутствовать.

Пример 3.

• <вещ. константа>::=

[<знак>]<целое>.<целое>[E [<знак>] целое>]

• <знак>::= + | -

• <целое>::=<цифра>|<целое><цифра>

• <цифра>::=0 | 1 | … | 9.

• Часть предложения, заключенная в фигурные скобки, может либо отсутствовать, либо повторяться любое число раз.

Пример 4

• <символическое имя>::= <буква> {<буква> | <цифра>}

• <буква>::= А | … | z

• <цифра>::= 0 | 1 | ... | 9

Пример 5

• <список имен>::= <имя> { , < имя> }

• Число повторений части предложения, заключенного в фигурные скобки, может быть ограничено снизу и сверху подстрочными и надстрочными индексами.

• Это записывается следующим образом: ,

где m – минимальное, n- максимальное число повторений.

Например, цепочка символов:

Определяет символическое имя длиной не более 6 символов.

• Третий распространенный способ описания синтаксиса языков программирования – это синтаксические диаграммы, являющиеся графическим изображением БНФ.

• Нетерминальные символы изображаются на СД в прямоугольниках, терминальные в кружках или овалах (для длинных терминальных символов).

• Символы соединяются стрелками, указывающими последовательность чтения символов, образующих цепочку.

• Символ или (“|”) изображается на диаграмме петлей.

Пример 6

Определение символического имени

• Символическое имя

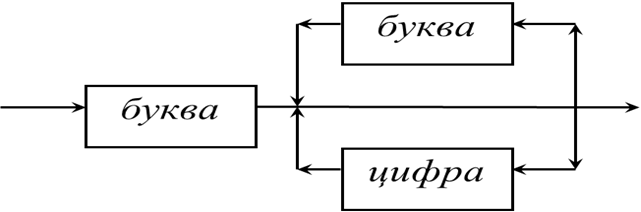
Цифра Буква

Пример 7

Определение синтаксиса оператора описания

Оператор описания

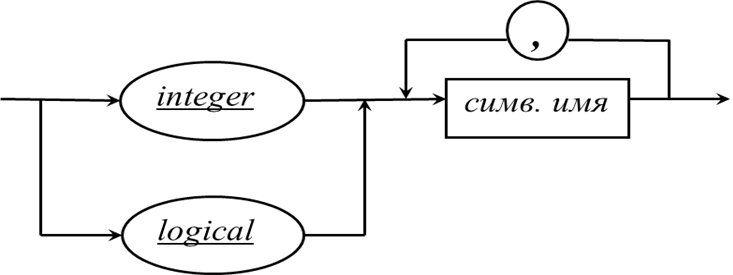
2. Порождающая грамматика (ПГ)

• Синтаксис всего языка или его части определяется последовательностью правил подстановки.

• Одно из этих правил, обозначающее наиболее общее (основное) понятие языка стоит первым,

• нетерминальный символ, обозначающий это понятие – начальный символ грамматики.

• Упомянутая последовательность правил подстановки называется порождающей грамматикой, так как она описывает процедуру получения правильных предложений языка.

---

1. Формальное определение ПГ

ФПГ G представляет собой четверку объектов:

где

• N - множество нетерминальных символов, обозначающих конструкции описываемого языка;

• T - множество терминальных символов, состоящих из букв алфавита описываемого языка;

• начальный символ грамматики, стоит в левой части первого правила подстановки;

• П – набор правил подстановки.

Таким образом, чтобы описать синтаксис ФЯ, необходимо задать

2. Словарь грамматики:

• множество цепочек терминальных и нетерминальных символов, включая пустую цепочку.

• множество цепочек терминальных и нетерминальных символов, исключая пустую цепочку.

Пошаговый процесс получения конструкций языка по ФПГ называется выводом или порождением.

Вывод заканчивается, если все символы терминальные.

Пример 8. Вывод по грамматике примера 1 цепочки символов -247.

<целое>::= <знак> <цифры>

- <цифры>

- <цифры> <цифра>

- <цифры> <цифра> <цифра>

- <цифра> <цифра> <цифра>

- 2 <цифра> <цифра>

- 24 <цифра>

- 247.

• Примеры вывода символических имён по грамматике 2:

1) <символическое имя> => <символическое имя> < буква-цифра> => <символическое имя> < буква-цифра> < буква-цифра> => <буква> < буква-цифра> < буква-цифра> => X< буква-цифра> < буква-цифра> => X <буква> <буква-цифра > => XY< буква-цифра > => XY<цифра> => XY9

2) <символическое имя> => <буква> => А

• В этом примере использован один очень простой прием – рекурсивное определение. В первом правиле подстановки <символическое имя> определяется вначале простейшим образом как <буква>, а потом, после разделителя | (“или”), нетерминальный символ <символическое имя> используется с определенным значением.

• После того, как <символическое имя> получило значение <буква> <буква-цифра>, на следующем шаге оно может быть определено как

<буква> < буква-цифра > < буква-цифра>

и так далее.

• Замечание:

• На любом шаге вывода можно по-разному раскрывать нетерминальные символы, если в правых частях правил подстановки присутствуют разделители “или”.

• Использование рекурсивного определения нетерминальных символов позволяет получить сколь угодно длинное предложение языка, так как рекурсия естественным образом обеспечивает повторяющийся (циклический) процесс.

• Вообще, если необходимо описать синтаксис сколь угодно длинной последовательности объектов, следует применять рекурсию.

<последовательность объектов> ::= <объект> | <последовательность объектов> < объект>

• Пример описания синтаксиса простого языка программирования.

• В этом описании можно найти все особенности использования БНФ, в частности описания синтаксиса арифметических и логических выражений, являющееся уже классическим.

• Пример. Грамматика языка программирования

• Вначале зададим некоторое неформальное описание этого языка.

• Язык позволяет оперировать с данными целого (integer) и логического типов (logical).

• Логические значения: true, false.

• Данное может быть константой, переменной или одномерным массивом целых чисел.

• Одномерный массив: array имя [n:m], где n,m – целые константы, определяющие нижнюю и верхнюю границы изменения индекса.

• Элемент массива записывается в виде:

---

имя [индексное выражение].

• Операторы языка:

  • оператор присваивания: x:=E;

  • условный оператор:

if условие then оператор else оператор fi или

if условие then оператор fi ;

• оператор цикла: while условие do оператор od;

• пустой оператор.

3. Формальное описание синтаксиса языка в БНФ

• <программа>::= <описания> <оператор>

• <описания> ::= <оператор описания>;|

<описания> <оператор описания>;

• <оператор описания>::= <оператор описания типа> | <оператор описания массива>

• <оператор описания типа>::=

<тип> <список типа>

• <тип >::= integer|logical

• <список типа>::= <имя> |

<список типа>,<имя>

• <оператор описания массива>::=

array <список массивов>

• <список массивов>::=

<элемент списка> | <список массивов>, <элемент списка>

• <элемент списка>::=

<имя>[<целое>:<целое>]

• <оператор>::= <оператор присваивания> | <условный оператор> | <оператор цикла> |

<пустой оператор> |

<оператор> ; <оператор>

• <оператор присваивания>::=

<переменная> := <выражение>

• <условный оператор>::= if < логическое выражение> then <оператор> fi|

if <логическое выражение> then <оператор> else <оператор> fi

• <оператор цикла>::= while < логическое выражение> do <оператор> od

• <пустой оператор>::=

• <переменная>::= < простая переменная >|

<переменная с индексом>

• < простая переменная >::= <имя>

• <переменная с индексом>::=

<имя> [ < арифметическое выражение> ]

• <выражение>::= < арифметическое выражение > | < логическое выражение >

• <арифметическое выражение> ::= <слагаемое> | + <слагаемое> |

- <слагаемое> | <арифметическое выражение> + <слагаемое> |

<арифметическое выражение> -

< слагаемое >

• <слагаемое>::= <множитель> | <множитель> * <слагаемое> |

<множитель> / <слагаемое>

• <множитель>::= <целое> | <переменная>|

(<арифметическое выражение>)|

<множитель> ** <множитель>

• <логическое выражение> ::=

<логическое слагаемое> | <логическое слагаемое> <логическое выражение>

• <логическое слагаемое>::=

<логический множитель> |

<логический множитель> <логическое слагаемое>

• <логический множитель>::= <логическая константа> | <простая переменная> |

<арифметическое выражение> <операция отношения> <арифметическое выражение> | (<логическое выражение>) |

<логический множитель>

• <логическая константа>::= <true> | < false>

• <операция отношения>::= |=|>|<| | |

• <имя>::= <буква> | <имя> <буква> | <имя> <цифра>

• <буква>::= A|B|…|z

<цифра>::= 0|1|…|9

3. Классификация языков по Хомскому

В основе этой классификации лежит форма левой и правой частей правила подстановки

U::=u.

По Хомскому языки делятся на 4 класса с номерами 0,1,2,3, причем каждый класс с большим номером является подмножеством любого класса с меньшим номером.

Класс 0. Грамматики с фразовой структурой

Правило подстановки имеет вид:

U::=u,

где U – произвольная непустая последовательность (цепочка) терминальных и нетерминальных символов;

---

Смотрите также файлы

• Контрольная работа по ИТПД.docx

• информационные технологии.doc

• Лабораторные информатика.doc

• Информатика.doc

• дипломная проектирование БД рекламного агентства.doc