Добавлен: 19.10.2018
Просмотров: 1314
Скачиваний: 6
u - произвольная (возможно и пустая) последовательность терминальных и нетерминальных символов.
Класс 0 является наиболее мощным, языки этого класса могут служить моделью естественных языков.
Класс 1. Контекстно-зависимые грамматики
Правило подстановки имеет вид:
x U y ::= x u y,
где U – нетерминальный символ;
x, u, y – произвольные последовательность (цепочка) терминальных и нетерминальных символов.
Смысл этого правила в том, что замена U на u осуществляется только в контексте x...y.
Класс 2. Контекстно-свободные грамматики
Правило подстановки имеет вид:
U::= u,
где U – ровно один нетерминальный символ;
u - произвольная цепочка терминальных и нетерминальных символов.
Грамматика типа 2 отличается от грамматики типа 1 тем, что замена U на u осуществляется в любом контексте.
Грамматика типа 2 обычно используется для описания синтаксиса языков программирования.
Класс 3. Автоматные (регулярные) грамматики
Правило подстановки имеет вид:
U::= t, U::= t n
где t – ровно один терминальный символ;
n – ровно один нетерминальный символ.
Грамматика типа 3 используется для описания синтаксиса простых языков программирования (узкоспециализированных или подмножеств языков программирования).
-
Следует иметь в виду, что если хотя бы одно правило подстановки в грамматике относится к более высокому классу (с меньшим номером), чем остальные, то и вся грамматика относится к этому классу.
-
Наибольший интерес в теории языков программирования представляют контекстно-свободные и автоматные грамматики. Одна из причин этого - сравнительная простота распознавания конструкций этих языков, что используется для разработки трансляторов.
-
Синтаксический анализ языковых конструкций
-
Синтаксический анализ языковых конструкций представляет собой задачу, противоположную задаче порождения (вывода).
-
Задача синтаксического анализа (задача разбора) формулируется следующим образом: определить, соответствует ли заданная конструкция некоторого языка грамматике этого языка или другими словами, является ли заданная конструкция правильным (не содержащим грамматических ошибок) предложением языка.
-
Задача разбора имеет широкое практическое применение, каждый транслятор языка программирования имеет в своём составе блок синтаксического анализа.
Прежде чем рассматривать алгоритмы синтаксического анализа, введём понятие синтаксического дерева, как графического способа изображения вывода конкретного предложения языка.
-
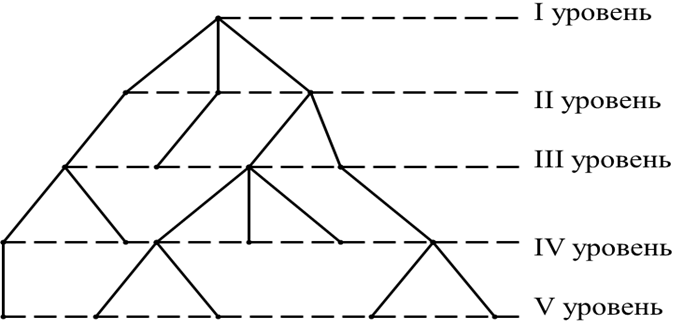
Дерево
-
представляет собой иерархическую структуру, состоящую из узлов разных уровней;
-
каждый из узлов некоторого уровня (кроме последнего) связан с несколькими узлами следующего уровня и не более, чем с одним узлом предыдущего уровня.
На
I уровне может быть только один узел,
называемый корнем.
Узлы последнего уровня называются
листьями.
Куст
узла
– множество подчиненных ему узлов
нижних уровней.
-
В синтаксических деревьях узлы представляют собой нетерминальные и терминальные символы,
-
листья являются терминальными символами, а остальные узлы – нетерминальными.
-
Корень дерева – начальный символ грамматики. Куст представляет собой правую часть правила подстановки для данного нетерминального символа.
Пример 1. Синтаксическое дерево для описания массива array A[0:10]
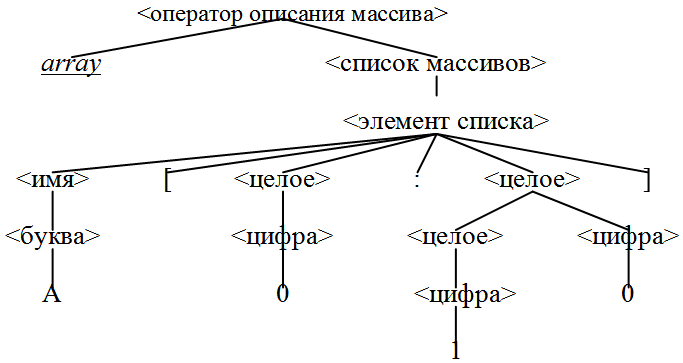
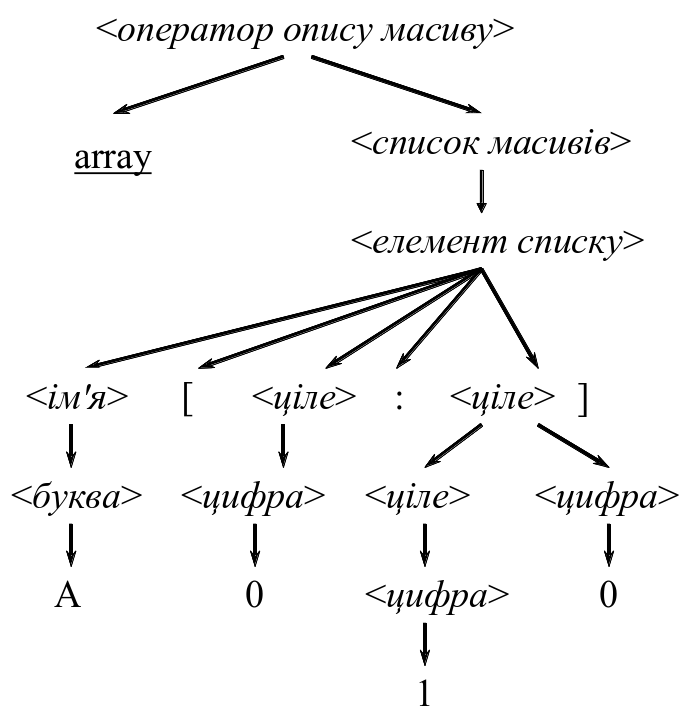
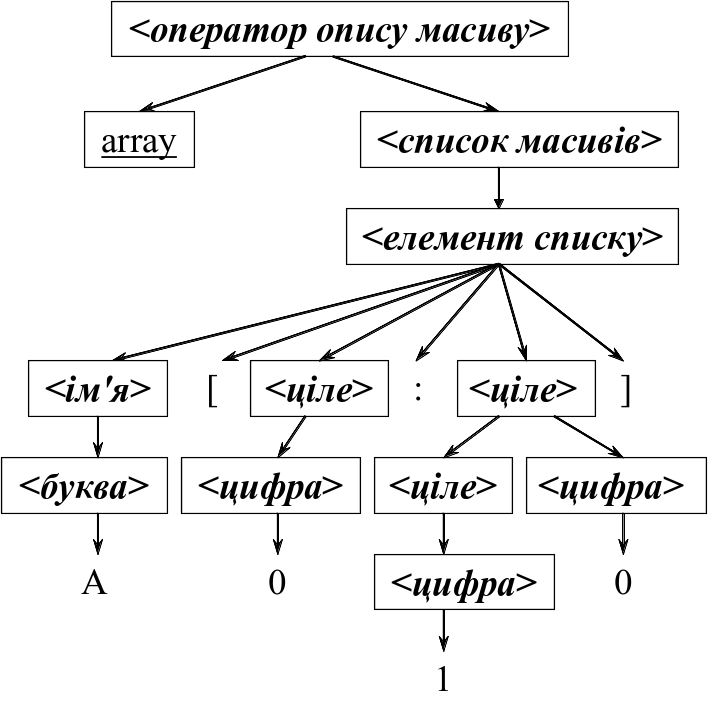
-
Последовательность листьев этого дерева, читаемая слева направо, представляет собой предложение array A[0:10].
-
Пример 2. Синтаксическое дерево для арифметического выражения A1*(A+B)
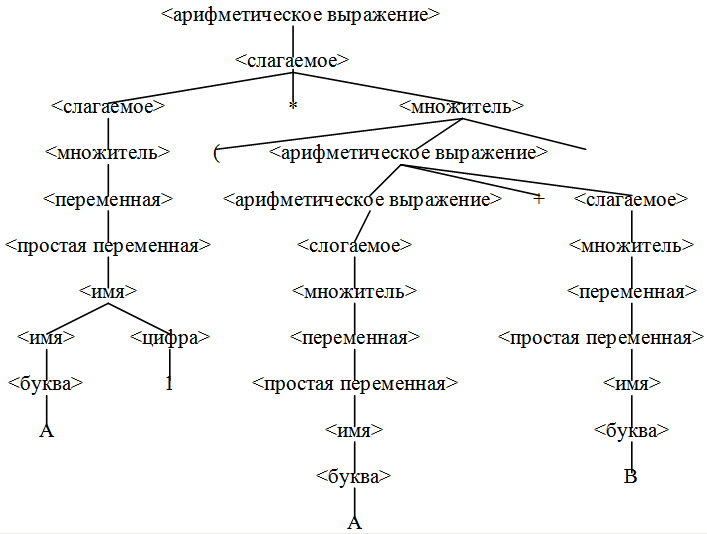
-
Достоинством синтаксических деревьев является наглядность описания синтаксиса как самого предложения, так и его отдельных составляющих.
-
С другой стороны, для реальных конструкций языков программирования дерево оказывается очень громоздким.
-
Поэтому, если дерево используется для получения наглядности описания, то, либо опускаются некоторые промежуточные уровни, несущественные для этого описания, либо оно составляется для простых предложений.
-
Идея построения деревьев широко используется в трансляторах, так как существуют эффективные методы отображения деревьев в памяти ЭВМ.
-
Синтаксический анализ предложений, записанных на языках программирования, фактически сводится к построению синтаксических деревьев различными методами.
-
Существуют два базовых алгоритма синтаксического анализа (решения задачи разбора):
-
нисходящий разбор (развёртка);
-
восходящий разбор (свёртка).
-
-
При нисходящем разборе синтаксическое дерево строится от корня к листьям.
-
Отличительная черта – целенаправленность, так как, отправляясь от нетерминального символа, мы стремимся найти такую подстановку, которая привела бы к части требуемой цепочки терминальных символов.
-
В простейших случаях синтаксический анализатор (распознаватель) пытается достичь этого путём направленного перебора различных вариантов.
-
Распознаватель рассматривает дерево сверху вниз и слева направо и выбирает первый нетерминальный символ, не имеющий подчиненных узлов (являющийся “листом”).
-
В списке правил подстановки отыскивается правило (или набор правил), которое в левой части содержит этот нетерминальный символ, а в правой части (в правых частях) – очередные (считая слева направо) символы анализируемого предложения.
-
Если такое правило есть, дерево наращивается и описанный процесс повторяется. Если правило не найдено, распознаватель возвращается на один или несколько шагов назад, пытаясь изменить выбор сделанный ранее.
-
Процесс разбора заканчивается в одном из двух случаях:
-
построено дерево, все листья которого являются терминальными символами, и при чтении слева направо образуют анализируемое предложение. В этом случае результат распознавания положителен, то есть синтаксис рассматриваемого предложения соответствует грамматике языка;
-
распознаватель переработал все возможные варианты последовательностей подстановок, но так и не пришёл к дереву, описанному в 1.
-
-
Это означает, что анализируемое предложение не принадлежит данному языку (то есть содержит ошибки).
-
Следует подчеркнуть, что ошибка считается выявленной только в том случае, когда рассмотрены все допустимые варианты подстановки.
Пример. Провести нисходящий синтаксический разбор числа +2.4 по грамматике
1) <константа> ::= <КФТ> | <знак> <КФТ>
2) <КФТ> ::= .<целое> | <целое>. | <целое>.<целое>
3) <целое> ::= <цифра> | <цифра> <целое>
4) <знак> ::= + | –
5) <цифра> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
-
Процесс разбора покажем в виде последовательности шагов, на каждом из которых строится какая-то часть дерева.
-
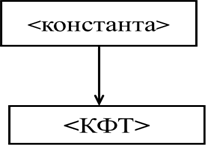
Шаг 1. Нетерминальный символ <константа> – корень дерева.
-
Шаг 2. Поскольку выражение 1) не содержит в правой части терминальных символов, выбираем первую слева цепочку символов:
-
<константа> ::= <КФТ>.
-
Получаем
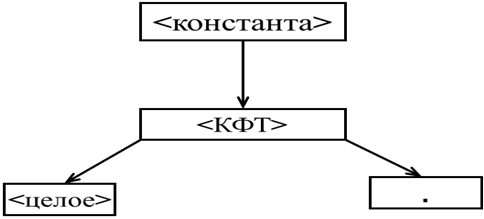
Шаг 3. В правиле 2) первая цепочка начинается с терминального символа “.”, а так как первый символ анализируемого предложения – “+”, эта цепочка не подходит. Выбираем следующую
-
Шаг 4. В правиле 3) выбираем первую цепочку <цифра>:
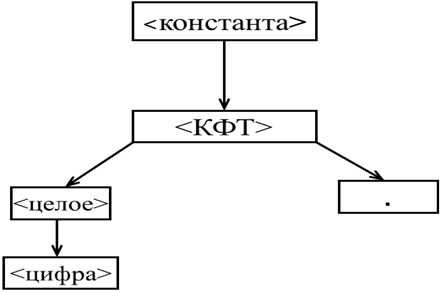
-
Шаг 5. Для определения нетерминального символа <цифра> по правилу 5) есть 10 терминальных символов, но ни один из них не совпадает с “+”.
-
Поэтому осуществляем возврат на один шаг назад и, снова пользуясь правилом 3), получаем:
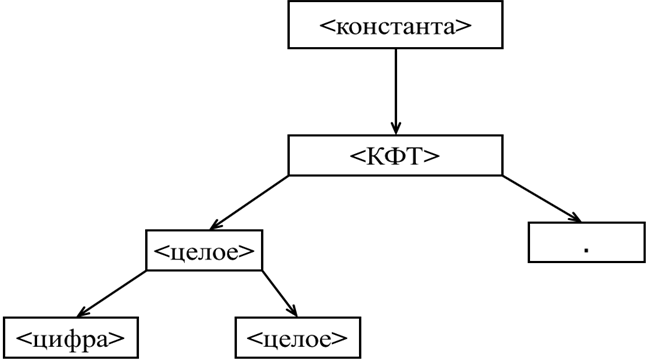
-
Шаг 6. Из двух ветвей дерева выбираем, согласно алгоритму, левую и снова пытаемся применить правило 5).
-
Так как невозможно, возвращаемся назад к дереву, полученному на шаге 2 (поскольку попытки применения правила 3) исчерпаны.
-
В правиле 2) выбираем цепочку <целое>.<целое>. Получаем:
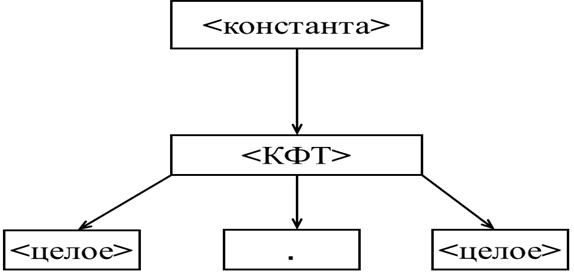
На этом пути мы, очевидно, сделаем ещё 2 шага, прежде чем убедимся в его ложности.
Шаг 9. Возвращается к правилу 1) и выбираем для подстановки вторую цепочку <знак><КФТ>
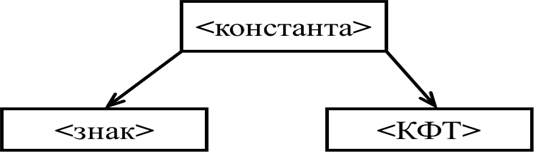
-
Шаг 10. Применяем правило 4) к нетерминальному символу <знак>. Получаем.
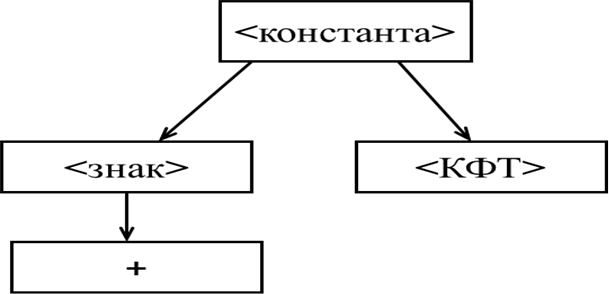
-
Полученный терминальный символ совпадает с первым символом анализируемого предложения, следовательно, ветвь полученного дерева правильна.
-
Далее пытаемся получить следующий символ –“2”.
-
Шаг 11. Раскрываем нетерминальный символ <КФТ> по правилу 2), при этом выбираем вторую цепочку, так как в первой символ “.” не совпадает с символом “2”.
-
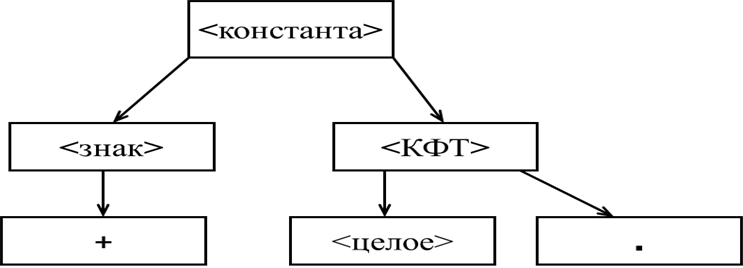
-
Шаги 12, 13. Применяем правила 3) и 5).
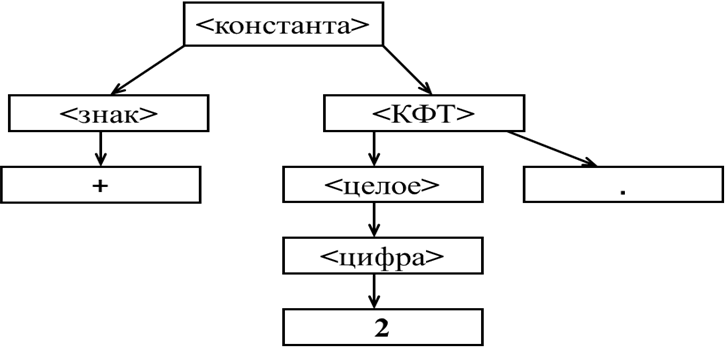
-
Получили сразу два терминальных символа анализируемого предложения “2” и “.”. Однако дерево уже построено, так как все листья являются терминальными символами. Если бы все варианты подстановок были уже испытаны, можно было бы сделать вывод, что в предложении +2.4 допущена ошибка. Поскольку это не так, делаем два шага назад, возвращаясь к дереву, полученному на Шаге 11.
-
Шаг 14. Снова применяем правило 3), но его вторую цепочку.
-
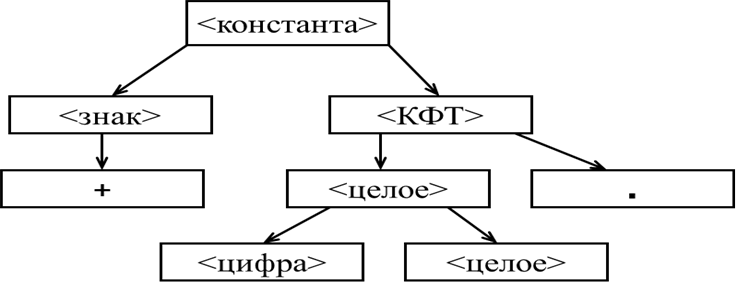
Очевидно, что на этом пути мы сделаем ещё 3 шага, прежде чем зайдём в тупик.
Пропускаем эти три шага и возвращаемся, наконец, к дереву, полученному на шаге 10.
-
Шаг 18. Применяем к символу <КФТ> на этом дереве правило 2) (третью цепочку).
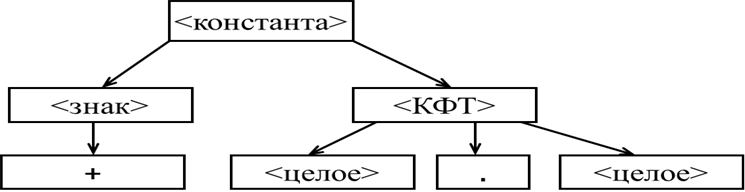
-
Шаги 19, 20, 21, 22.
-
Раскрываем последовательно левый и правый символы <целое>
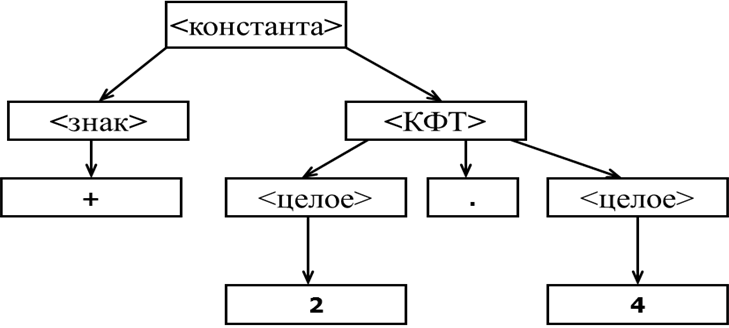
Листья этого дерева (слева направо) образуют исходное предложение +2.4, следовательно оно соответствует заданной грамматике, т.е. не содержит ошибок.
Всегда следует иметь ввиду, что только неукоснительное, точное следование алгоритму нисходящего разбора позволяет гарантировать правильность разбора, особенно для сложных грамматик. Попытки пропустить несколько шагов как очевидные или сделать их “в уме” часто приводят к ошибкам.
-
Примечание. Описанный алгоритм нисходящего разбора неприменим, если грамматика является леворекурсивной, то есть содержит правила подстановки вида
U ::= Uu,
поскольку при этом попытки раскрыть самый левый нетерминальный символ приведут к бесконечному порождению нетерминального символа U. В таком случае необходимо видоизменить алгоритм, сделав его, например, правосторонним, или изменить грамматику.
-
Синтаксический анализ конструкций языков программирования
-
В алгоритме нисходящего разбора не обязательно строить дерево. На каждом шаге можно записывать цепочку нетерминальных и терминальных символов, полученных после очередной подстановки.
-
При восходящем разборе дерево строится от листьев к корню, то есть алгоритм, отправляясь от заданной строки, пытается, применяя правила подстановки справа налево, привести её к начальному символу грамматики.
-
Часть строки, которую можно привести к не терминальному символу, называется фразой.
-
Если приведение осуществляется применением одного правила подстановки, фраза называется непосредственно приводимой.
-
Самая левая непосредственно приводимая фраза называется основой.
-
Алгоритм восходящего разбора
В исходном предложении отыскивается основа (то есть просмотр, как и в нисходящем разборе, идет слева направо) и приводится к нетерминальному символу.
-
Эта операция применяется до тех пор, пока либо получен единственный символ, являющийся начальным символом грамматики (в этом случае разбор заканчивается успешно), либо в полученной цепочке не может быть найдена фраза.
-
В этом случае делается возврат на один или несколько шагов назад и выбирается другая основа.
-
Если все возможные варианты перебраны, а корень дерева так и не получен, делается вывод о наличии ошибки в разбираемом предложении, и алгоритм прекращает работу.
-
Таким образом, восходящий разбор представляет собой перебор вариантов, однако не целенаправленный, так как нет возможности отбрасывать заведомо неправильные подстановки, как это имеет место в нисходящем разборе (цепочка “.<целое>” в правиле 2), неподходящие цифры в правиле 5) в предыдущем примере.
-
Процесс восходящего разбора записывают либо в виде построения дерева от листьев к корню, либо в виде последовательности цепочек терминальных и нетерминальных символов, начинающейся с анализируемого предложения, заканчивающейся (если предложение не содержит ошибок) начальным символом грамматики.
-
Пример. Провести восходящий синтаксический разбор выражения 5*I+J по грамматике
-
1) <выражение> ::= <слагаемое> | <слагаемое>+<имя> | <слагаемое>–<имя> | <слагаемое>+<целое> | <слагаемое>–<целое>
-
2) <слагаемое>::= <имя> | <целое> | <целое>*<имя>
-
3) <целое> ::= <цифра> | <целое><цифра>
-
4) <имя> ::= I | J | K | L | M | N
-
5) <цифра>::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
-
Разбор представим в виде последовательности шагов, на каждом из которых будет получена цепочка символов, непосредственно приводимые фразы будем подчёркивать. Справа в скобках указаны номера правил, по которым произведена подстановка.
-
Шаг 1. Исходное предложение.
-
Шаг 2. <цифра>*I+J 5)
-
Шаг 3. <целое>*I+J 3)
-
Шаг 4. <слагаемое>*I+J 2)
-
Шаг 5. <выражение>*I+J 1)
-
Шаг 6. <выражение>*<имя>+J 4)
-
Шаг 7.<выражение>*<слагаемое>+J 2)
-
Шаг 8. <выражение>*<выражение>+J 1)
-
Шаг9.<выражение>*<выражение>+<имя> 4)
-
Шаг10. <выражение>*<выражение>
-
+<слагаемое> 2)
-
Шаг11.<выражение>*<выражение>+
-
<выражение> 1)
-
В полученной цепочке нет фразы. Изменить выбор непосредственно приводимой фразы можно, вернувшись к цепочке, полученной на шаге 7:
-
<выражение>*<слагаемое>+J.
-
Шаг 12. <выражение>*<слагаемое>+
-
<имя> 4)
-
Шаг 13. <выражение>*<выражение> 1)
-
В полученной цепочке нет фразы.
-
Возвращаемся к шагу 12 <выражение>*<слагаемое>+<имя>.
-
Шаг 14. выражение>*<слагаемое>+
-
<слагаемое> 2)
-
Шаг 15. <выражение>*<выражение>+
-
<слагаемое> 1)
-
Получили ту же цепочку, что и на шаге 10. Возвращаемся к шагу 14, сделаем один ложный шаг, затем к шагу 6: <выражение>*<имя>+J.
-
Шаг 17. <выражение>*<имя>+<имя> 4)
-
Шаг 18. <выражение>*<слагаемое>+
-
<имя> 2)
-
Возвращаемся к шагу 17.
-
Шаг 19. <выражение>*<имя>+
-
<слагаемое> 2)
-
Шаг 21. <выражение>*I+<имя> 4)
-
Возвращаемся к шагу 4: <слагаемое>*I+J
-
Шаг 25. <слагаемое>*<имя>+J 4)
-
Далее проделаем ещё 18 ложных шагов, после чего вернёмся к шагу 3: <целое>*I+J.
-
Шаг 44. <целое>*<имя>+J 4)
-
Шаг 45. <слагаемое>+J 2)
-
Шаг 46. <выражение>+J 1)
-
…
Шаг 49. <выражение>+<выражение> 1)
Возвращаемся к шагу 45.
Шаг 50. <слагаемое>+<имя> 4)
Шаг 51. <выражение>
-
Главным недостатком как нисходящего, так и восходящего алгоритмов разбора является большое количество шагов, что определяется переборным характером алгоритмов.