Вычисление определенных интегралов методом прямоугольников

При вычислении определенного интеграла методом прямоугольников подынтегральная функция f(x) на интервале интегрирования заменяется полиномом нулевой степени, т.е. константой. Вычисление определенного интеграла по методу прямоугольников сводится к вычислению площади прямоугольника, одна из сторон которого – длина отрезка интегрирования (или шаг разбиения по оси х), другая – высота прямоугольника (вычисляется по значению функции в начале, в конце или в середине интервала интегрирования. В зависимости от этого и метод называется: метод левых, правых или средних прямоугольников). Будем линейно аппроксимировать функцию f(x) на некотором разбиении отрезка [a,b] на n частей.

Формула для приближенного вычисления интеграла будет иметь вид:

где S_i = f_i*h_i – площадь i – го прямоугольника, f_i - значение функции в некоторой точке внутри i – го отрезка, h_i – ширина этого отрезка. В частном случае, когда все отрезки имеют одинаковую ширину, h_i = h =(b-a)/n.

Если высота i – го прямоугольника вычисляется по значению подынтегральной функции в левой границе прямоугольника – этот метод называется методом левых прямоугольников, соответственно при вычислении высоты прямоугольника по значению подынтегральной функции в правой границе прямоугольника называют методом правых прямоугольников.

Метод правых (рис.1) и левых (рис.2) прямоугольников имеет сравнительно высокую погрешность.

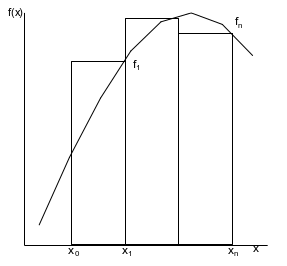
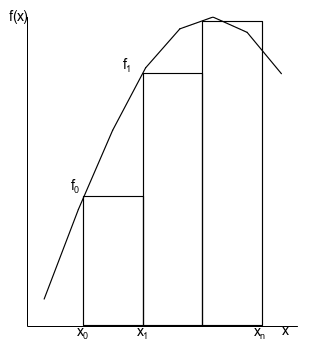
Рис. 1 Метод правых прямоугольников. Рис.2 Метод левых прямоугольников.

Если функция на всем интервале интегрирования возрастает, тогда метод левых прямоугольников дает заниженное значение интеграла, а метод правых прямоугольников – завышенное значение, и наоборот, если функция убывающая, то метод левых прямоугольников дает завышенное, а метод правых прямоугольников – заниженное значение интеграла.

Более низкую погрешность имеет метод средних прямоугольников (рис.3), в котором высота прямоугольников вычисляется по значению подынтегральной функции в середине отрезка интегрирования. В этом случае S_i = f((x_i+1 - x_i )/2)*(x_i+1 - x_i ) или, в случае равномерной сетки, S_i = f(x_i +h/2)*h

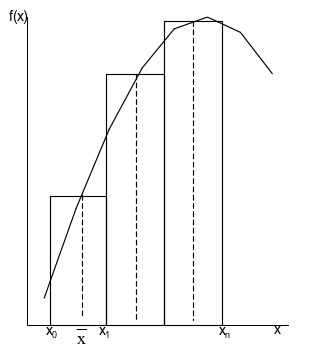
Рис. 3 Метод средних прямоугольников.

Описание алгоритма вычисления определенного интеграла методом прямоугольников:

n=значение

а=значение

b=значение

h=(b-а)/n

s=0

s1=0

s2=0

Цикл по х от а до b-h с шагом h

s=s+f(x)*h && метод левых прямоугольников

s1=s1+f(x+h)*h && метод правых прямоугольников

s2=s2+f(x+h/2)*h && метод средних прямоугольников

КонецЦикла

Печать s, s1, s2

ЗадатьФункцию F

Параметры x

Вернуть (выражение подынтегральной функции от x)

Пример решения на языке VFP:

clear

k=2

?k^3/3

n=500

a=0

b=2

h=(b-a)/n

s=0

s1=0

s2=0

FOR x=a TO b-h STEP h

s=s+f(x)*h &&метод левых прямоугольников

s1=s1+f(x+h)*h &&метод правых прямоугольников

s2=s2+f(x+h/2)*h &&метод средних прямоугольников

endfor

?"s=",s," s1=",s1, "s2=", s2

---

FUNCTION f

PARAMETERS x

RETURN x^2

Пример решения на языке VBA:

Sub sub1()

k = 2

Debug.Print k ^ 3 / 3

n = 500

a = 0

b = 2

h = (b - a) / n

s = 0

s1 = 0

s2 = 0

For x = a To b - h Step h

‘метод левых прямоугольников

s = s + f(x) * h

‘метод правых прямоугольников

s1 = s1 + f(x + h) * h

‘метод средних прямоугольников

s2 = s2 + f(x + h / 2) * h

Next

Debug.Print "s=", s, " s1=", s1, "s2=", s2

End Sub

Function f(x)

f = x ^ 2

End Function

Вычисление определенных интегралов методом трапеций

Вычисление определенного интеграла по методу трапеций сводится к вычислению площади фигуры, ограниченной осью абсцисс, графиком подынтегральной функции и прямыми x = a и x = b. Будем линейно аппроксимировать функцию f(x) на некотором разбиении отрезка [a,b] на n частей.

Формула для приближенного вычисления интеграла будет иметь вид:

где S_i = (f_i-1 +f_i)*h/2 – площадь i – й трапеции, где h=(b-a)/n.

Если раскрыть скобки в выражениях для S_i, то формула для вычисления интеграла примет вид:

Описание алгоритма вычисления определенного интеграла методом трапеций:

n=значение

а=значение

b=значение

h=(b-а)/n

s=0

Цикл по х от а до b-h с шагом h

s=s+(f(x)+f(x+h))*h/2

КонецЦикла

Печать s

Задать_Функцию F

Параметры x

Вернуть (выражение подынтегральной функции от x)

Пример решения на языке VFP:

clear

k=2

?k^3/3

n=500

a=0

b=2

h=(b-a)/n

s=0

FOR x=a TO b-h STEP h

s=s+(f(x)+f(x+h))*(h/2)

endfor

?s3

FUNCTION f

PARAMETERS x

RETURN x^2

Пример решения на языке VBA:

Sub sub1()

k = 2

Debug.Print k ^ 3 / 3

n = 500

a = 0

b = 2

h = (b - a) / n

s = 0

For x = a To b - h Step h

s=s+(f(x)+f(x+h))*(h/2)

Next

Debug.Print "s=", s

End Sub

Function f(x)

f = x ^ 2

End Function

Вычисление интеграла по методу Симпсона

Метод Симпсона применяется для вычисления определенных интегралов вида I=.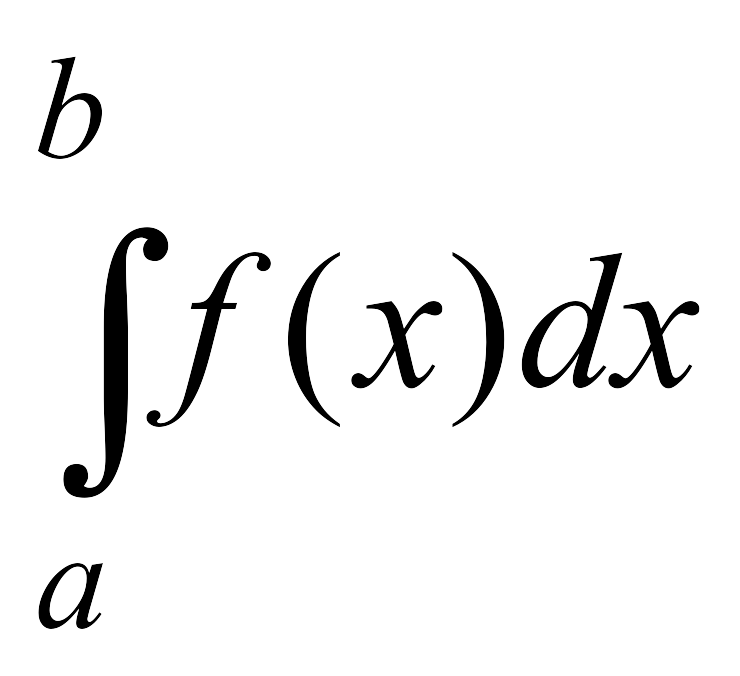

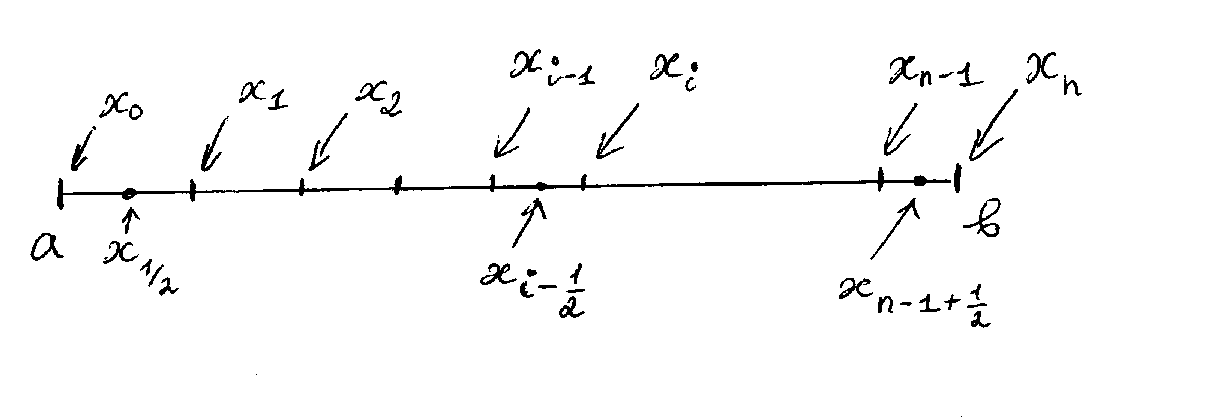
Разобьем отрезок [a, b] на n точек.

Представим искомый интеграл в виде суммы интегралов: 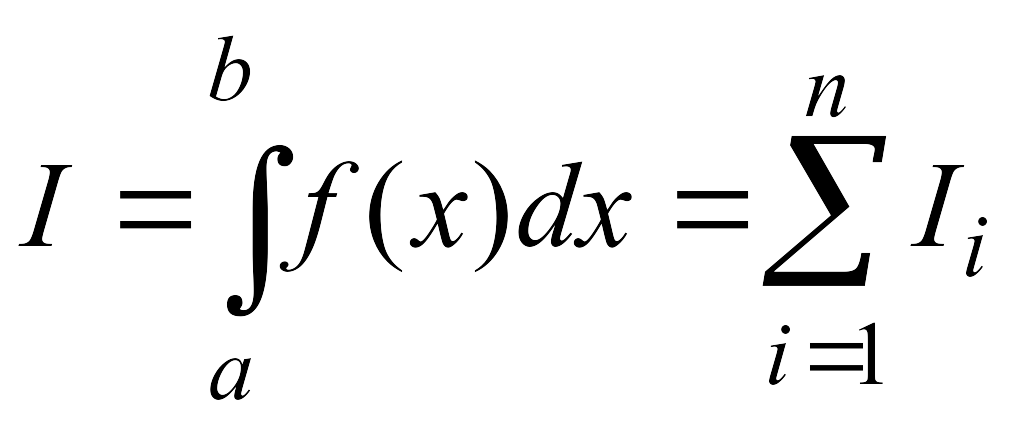, здесь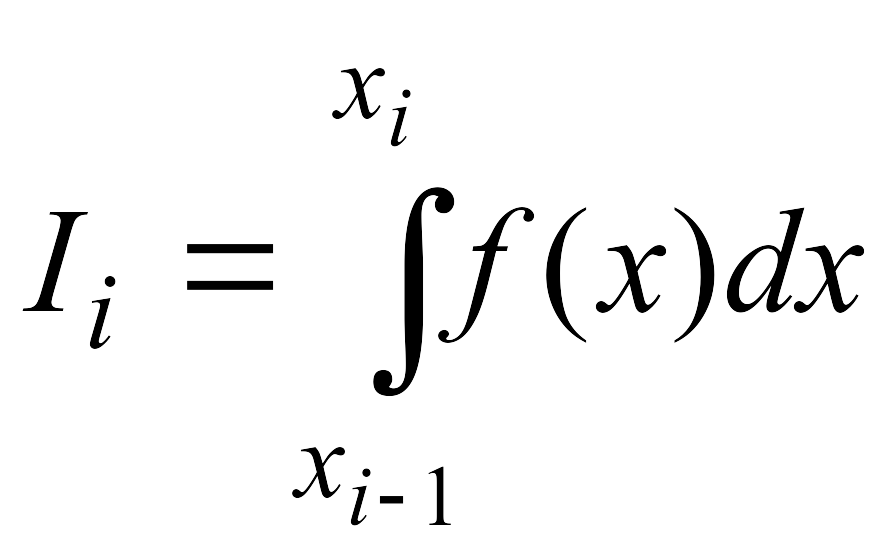

Р
ассмотрим i-ый отрезок [x_i-1, x_i]

x_i-1/2=(x_i+x_i-1)/2 – середина i-го отрезка

Представим на отрезке [x_i-1, x_i] подынтегральную функцию f(x) в виде полинома третьей степени P_i(x). Этот полином должен быть равен значениям подынтегральной функции в точках сетки и в середине отрезка: P_i(x_i-1) = f(x_i-1) – равенство полинома значению функции на левой границе i-го отрезка, P_i(x _i-1/2) = f(x_i-1/2), P_i(x _i) = f(x_i).

Такой полином можно записать, например, следующим образом:

P_i(x)=a+b(x-x_i-1)+c(x-x_i-1)(x-x_i-1/2),

здесь a, b, c – неизвестные коэффициенты, подлежащие определению.

Введем обозначение для ширины i-го отрезка: h_i=x_i-x_i-1,

тогда (x-x_i-1/2)= h_i/2, а (x_i-1/2-x _i-1)= h_i/2.

Запишем значения полинома на левой, правой границах и в середине i-го отрезка

P_i(x _i) = a+b*h_i+c*h_i*h_i/2 = f(x _i)= f_i (1)

P_i(x _i-1) = a = f(x _i-1)= f_i-1 (2)

P_i(x _i-1/2)= f(x _i-1/2)= a+b*h_i/2 = f_i-1/2 (3)

Из соотношения (2) следует a= f_i-1,

из выражения (3) легко увидеть, что b= h_i (f_i-1/2 - f_i)/2,

из выражения (1) получаем c=2 (f_i-a-b h_i)/h_i², подставим в выражение для коэффициента c выражения для коэффициентов a и b, в результате получим:

c=2(f_i - f_i-1) /h_i² – (2/h_i)(2/h_i) (f_i-1/2- f_i-1),

c=2 [f_i - f_i-1-2 f_i-1/2+2 f_i-1] /h_i²,

c=2 [f_i -2 f_i-1/2+f_i-1] /h_i².

Подставим найденные коэффициенты a, b, c в выражение для полинома:

P_i(x )= f_i-1 + 2 (f_i-1/2- f_i-1)( x -x _i-1) /h_i + 2 [f_i -2 f_i-1/2+f_i-1] ( x -x _i-1) ( x -x _i-1/2)/h_i²

Перейдем от переменной x к переменной t= x -x _i-1

Тогда dt = dx, а при x = x _i-1; t=0, при x = x _i; t=h_i при

x = x _i-1/2=x-( x_i -x _i-1)/2= x-x_i/2 -x _i-1/2= x- x _i-1+x _i-1/2-x_i/2=t-h_i/2

---

Тогда на i-ом интервале значение интеграла с учетом введенных обозначений, можно записать:

S_i=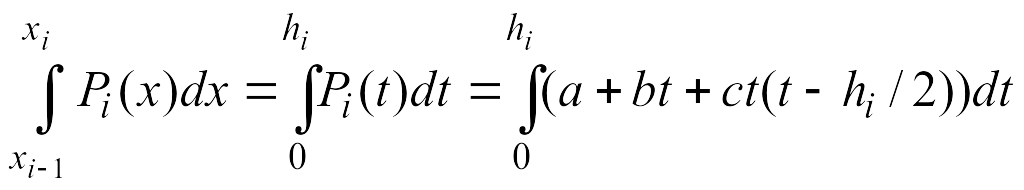=at+bt²/2+ct³/3-ct²h_i/4 =

=ah_i+bh_i²/2+ch_i³/3-ch_i³/4 = ah_i+bh_i²/2+ch_i³(1/3-1/4)= ah_i+bh_i²/2+ch_i³/12 =

= f_i-1h_i+ (h_i²/2)(f_i-1/2-f_i-1)/(h_i²/2)+ (h_i³/12)(2/h_i²)(f_i-2f_i-1/2+ f_i-1)=

= f_i-1h_i+ h_if_i-1/2- h_i f_i-1+(h_i/6)(f_i-2f_i-1/2+ f_i-1)=

= f_i-1h_i+(h_i/6) f_i-1 - f_i-1 h_i+h_i f_i-1/2-(h_i/3)f_i-1/2+(h_i/6) f_i=

=(h_i/6) f_i-1+ (2h_i/3)f_i-1/2+(h_i/6) f_i

Таким образом,

S_i= (h_i/3)( f_i-1/2+2 f_i-1/2 +f_i/2)

S_i - представляет собой значение интеграла на i-ом отрезке. Для получения интеграла на отрезке от a до b, необходимо сложить все S_i

Если h_i=h для любого i=1,…, N, тогда S_i= (h_i/3)( f_i-1/2+2 f_i-1/2 +f_i/2) и формулу Симпсона можно упростить

(4)

Формулу (4) можно упростить, для этого раскроем скобки в выражении под знаком суммирования

Выделим из первой суммы значение функции в точке x=a

,

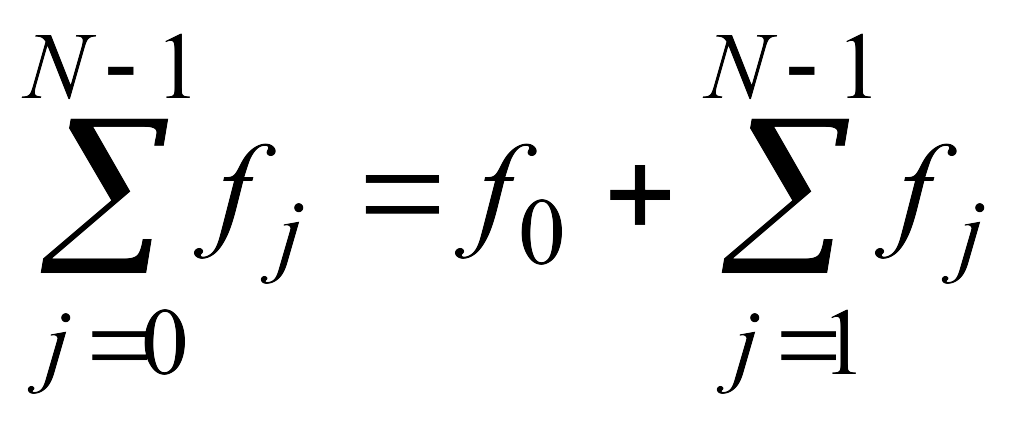а из последней суммы – значение функции в точке x=b

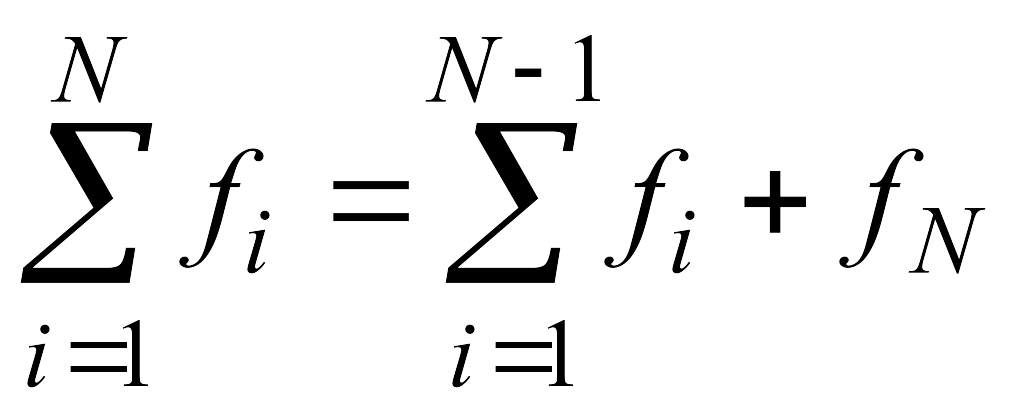
В результате получаем рабочую формулу Симпсона для равномерной сетки.

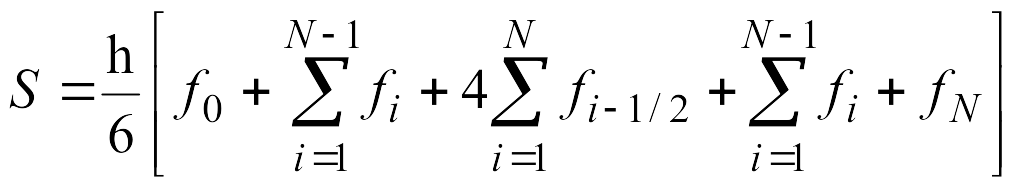
или

Учтем, что , , получим окончательное выражение для формулы Симпсона

(5)

В первой сумме формулы (5) вычисляют сумму значений функции во всех внутренних узлах отрезка [a, b], вторая сумма вычисляет сумму значений функции в средних точках i-ых отрезков.

Если середины отрезков включить в сетку наряду с узлами, тогда новый шаг h₀ = h/2 = (b-a)/(2*n), а формула (5) может быть записана в виде:

(6)

Рассмотрим . Значение данного интеграла легко найти аналитически и оно равно -0,75. Метод Симпсона для подынтегральной функции в виде полинома степени 3 и ниже дает точное значение.

Алгоритм вычисления этого интеграла методом Симпсона (формула (5) ).

a=0

b=1

n=5

h=(b-a)/n

f0=f1(a)

fn=f1(b)

s1=0

x1=a+h

цикл по i от 1 до n-1

s1=s1+f1(x1)

x1=x1+h

конец цикла

x2=a+h/2

s2=0

цикл по I от 1 до n

s2=s2+f1(x2)

x2=x2+h

конец цикла

s=h*(f0+2*s1+4*s2+fn)/6

Печать s

функция f1

параметры x

возврат x^3+3*x^2 + x*4 - 4

Пример программы вычисления интеграла методом Симпсона на языке VFP (по формуле (6)).

CLEAR

SET DECIMALS TO 10

? "I=",simpson(0,2,20)

x=2

? "I=",x^3/3

PROCEDURE simpson

PARAMETERS a,b,n

h=(b-a)/n

S_четные=0

S_нечетные=0

for x=a+h TO b-h STEP 2*h

S_нечетны = S_нечетные + 4*f(x)

NEXT

for x=a+2*h TO b-h STEP 2*h

S_четные = S_четные + 2*f(x)

NEXT

S=f(a)*h/3+(S_четные+S_нечетные)*h/3+f(b)*h/3

RETURN s

FUNCTION f

PARAMETERS x

RETURN x^2

Пример решения на языке VBA:

'процедура проверки правильности вычисления значения интеграла по его первообразной

Sub integ()

x = 2

i = x ^ 3 / 3

Debug.Print i

End Sub

Function f(x)

f = x ^ 2

End Function

Sub simpson()

a = 0

b = 2

n = 30

x = 2

h = (b - a) / n

s_четные = 0

s_нечетные = 0

For x = a + h To b - h Step 2 * h

s_нечетные = s_нечетные + 4 * f(x)

Next

Debug.Print "s_нечетные = " & s_нечетные

For x = a + 2 * h To b - h Step 2 * h

s_четные = s_четные + 2 * f(x)

Next

Debug.Print "s_четные=" & s_четные

s = h / 3 * (f(a) + (s_четные + s_нечетные) + f(b))

Debug.Print "n=" & n & " s=" & s

End Sub

---

Смотрите также файлы

• Аппроксимация выборки случайных чисел методом наименьших квадратов.doc

• Cлучайные величины.doc

• А.Т. Зуб Управление проектами.pdf

• Тема 7 Экономический эффект.pdf

• Тема 6 Создание рабочей группы инновационного проекта .docx