Файл: Выбор управленческого решения методом анализа иерархий. Оценить корректность метода на примере конкретной организации.pdf

В результате выполнения первого этапа предвидения – предварительного изучения проблемы методами сканирования и мозгового штурма были выявлены факторы, влияющие на использование космической информации ДЗЗ в разных отраслях хозяйственной деятельности. Во-первых, с помощью ГИС выполняется структурно-текстурный анализ, поиск и интеграция разных данных. Каждое из этих программных средств ГИС характеризуется с точки зрения объемов возможного использования космической информации ДЗЗ в виде электронных планов или цифровых карт: геологическое строение, гидрография и гидрология, природные или техногенные ландшафты.

Во-вторых, в пределах одной отрасли используется информация, полученная космическими аппаратами. Важность используемой в каждой отрасли космической информации ДЗЗ зависит от информационных характеристик космической информации, которые определяются параметрами космических аппаратов. К последним относятся определение площадей объектов в видимом, инфракрасном (ИК) и радио спектральных диапазонах, получение изображений с высоким разрешением в указанных диапазонах, - получение разновременных изображений объектов с высокой периодичностью.

Целью является определение относительного преимущественного спроса космической информации ДЗЗ в таких отраслях как сельское хозяйство, экология и чрезвычайные ситуации (ЧС), природные ресурсы, городское хозяйство, геодезия и картография.

Оценивание величин относительного спроса на космическую информацию ДЗЗ в указанных отраслях народного хозяйства осуществлялось несколькими модификациями МАИ в соответствии с иерархией факторов, представленной на рис.7.

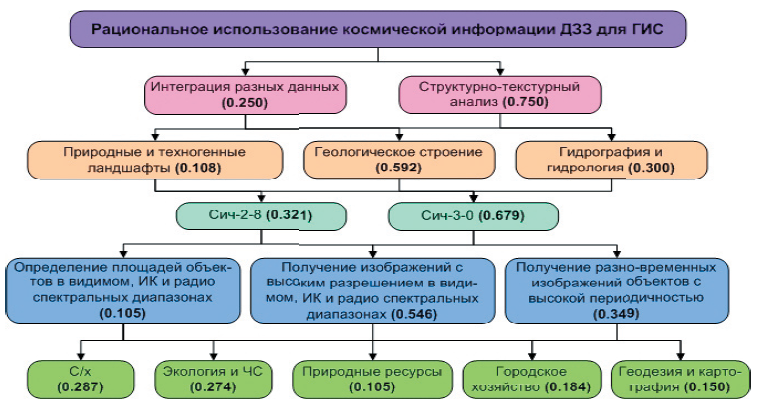Рисунок 7 - Иерархия факторов оценивания спроса на космическую информацию ДЗЗ с помощью МАИ^[25]

Цифры на этой иерархии соответствуют коэффициентам важности каждого из факторов относительно главной цели принятия решения – рационального использования космической информации ДЗЗ.

Результаты, полученные разными модификациями МАИ, свидетельствуют о том, что отрасли «сельское хозяйство», «экология» и «чрезвычайные ситуации» имеют наибольший спрос на космическую информации ДЗЗ по сравнению с другими исследуемыми отраслями хозяйственной деятельности.

Выводы

Таким образом, в работе рассмотрен системный подход к оцениванию достоверности решения, полученного МАИ, который включает модифицированные МАИ обработки нечетких экспертных оценок и оценивания ситуационных рисков задачи принятия решений, комплексное оценивание чувствительности полученного решения.

Приведен опыт применения МАИ для решения практических задач муниципального образования. Описанные модифицированные методы анализа иерархий используются в методологии сценарного анализа на этапе качественного анализа при решении задач предвидения.

Заключение

Метод анализа иерархий (МАИ) — это научно-обоснованный с позиции системного анализа подход в принятии решений для выбора альтернативы из множества возможных на основе нескольких критериев. Данный метод может использоваться для решения задач управления, в том числе задач прогнозирования и стратегического планирования. МАИ позволяет упорядочить работу лица, принимающего решение, и учесть достаточно сложную систему факторов, влияющих на выбор решения.

Системный подход к оцениванию достоверности решения, полученного МАИ, включает модифицированные МАИ обработки нечетких экспертных оценок и оценивания ситуационных рисков задачи принятия решений, комплексное оценивание чувствительности полученного решения.

Модифицированные методы анализа иерархий используются в методологии сценарного анализа на этапе качественного анализа при решении задач предвидения.

В работе рассмотрены две практически задачи, решение которых возможно с использованием МАИ.

1. Выявление путей решения проблем муниципального образования (на примере города Санкт-Петербург), к которым в первую очередь относятся проблемы социальной сферы, экологии, земельных ресурсов, предпринимательства, инвестиций и инноваций. Отобраны следующие проекты: строительство двух мусороперерабатывающих заводов; строительство второй нити Главного канализационного коллектора; строительство лечебно-диагностического корпуса городского центрального противортуберкулезного диспансера; реконструкция станции аэрации; строительство и реконструкция линий метрополитена. Использование МАИ позволило сделать вывод, что первоочередными для реализации являются проекты построения двух мусороперерабатывающих заводов, второй нити Главного канализационного коллектора и реконструкция станции аэрации. Второй приоритет получили проекты строительства и реконструкции линий метрополитена. Остальные мероприятия получили третий приоритет.

2. Оценивание направлений рационального использования космической информации дистанционного зонирования земли для геоинформационных систем. МАИ позволяет определить направления рационального использования космической информации дистанционного зондирования земли (ДЗЗ) при решении тематических заданий на основе геоинформационных систем (ГИС). Оценивание величин относительного спроса на космическую информацию ДЗЗ в указанных отраслях народного хозяйства осуществлялось несколькими модификациями МАИ в соответствии с иерархией факторов. Результаты, полученные разными модификациями МАИ, свидетельствуют о том, что отрасли «сельское хозяйство», «экология» и «чрезвычайные ситуации» имеют наибольший спрос на космическую информации ДЗЗ по сравнению с другими исследуемыми отраслями хозяйственной деятельности.

Список литературы

1. Грешилов, А. А. Математические методы принятия решений: Учеб. пособие / А. А. Грешилов. - Москва: Изд-во МГТУ. 2006.
2. Катулев А. Н. Математические методы в системах поддержки принятия решений: Учеб пособие / А. Н. Катулев, Н. А. Северцев. — М.: Высшая школа. 2005.
3. Кравченко Ю.А. Метод создания математических моделей принятия решений в многоагентных подсистемах // Известия ЮФУ. Технические науки. – 2011. – № 7 (120). – С. 141-145.
4. Ногин В. Д. Принятие решений в многокритериальной среде: количественный подход / В.Д. Ногин. - Изд. 2-е. испр. и доп. - М.: ФИЗМАТЛИТ. 2005.
5. Панкратова Н.Д., Недашковская Н.И. Методология обработки нечеткой экспертной информации в задачах предвидения. Часть 1 // Проблемы управления и информатики. – 2007. - №2 - С. 40 – 55.
6. Панкратова Н.Д., Недашковская Н.И. Методология обработки нечеткой экспертной информации в задачах предвидения. Часть 2 // Проблемы управления и информатики. – 2007. - №3 - С. 49 – 63.
7. Саати Т. Принятие решений. Метод анализа иерархии. - М.: Радио и связь, 1993.

1. Кравченко Ю.А. Метод создания математических моделей принятия решений в многоагентных подсистемах // Известия ЮФУ. Технические науки. – 2011. – № 7 (120). – С. 141-145. ↑

2. Кравченко Ю.А. Метод создания математических моделей принятия решений в многоагентных подсистемах // Известия ЮФУ. Технические науки. – 2011. – № 7 (120). – С. 141-145. ↑

3. Кравченко Ю.А. Метод создания математических моделей принятия решений в многоагентных подсистемах // Известия ЮФУ. Технические науки. – 2011. – № 7 (120). – С. 141-145. ↑

4. Ногин В. Д. Принятие решений в многокритериальной среде: количественный подход / В.Д. Ногин. - Изд. 2-е. испр. и доп. - М.: ФИЗМАТЛИТ. 2005. - С. 60. ↑

5. СППР Expert Choice // www.expertchoice.com. ↑

6. Саати Т. Принятие решений. Метод анализа иерархии. - М.: Радио и связь, 1993. – С. 5. ↑

7. Ногин В. Д. Принятие решений в многокритериальной среде: количественный подход / В.Д. Ногин. - Изд. 2-е. испр. и доп. - М.: ФИЗМАТЛИТ. 2005. - С. 60. ↑

8. Ногин В. Д. Принятие решений в многокритериальной среде: количественный подход / В.Д. Ногин. - Изд. 2-е. испр. и доп. - М.: ФИЗМАТЛИТ. 2005. - С. 60. ↑

9. Ногин В. Д. Принятие решений в многокритериальной среде: количественный подход / В.Д. Ногин. - Изд. 2-е. испр. и доп. - М.: ФИЗМАТЛИТ. 2005. - С. 60. ↑

10. Панкратова Н.Д., Недашковская Н.И. Методология обработки нечеткой экспертной информации в задачах предвидения. Часть 1 // Проблемы управления и информатики. – 2007. - №2 - С. 40 – 55. ↑

11. Панкратова Н.Д., Недашковская Н.И. Методология обработки нечеткой экспертной информации в задачах предвидения. Часть 2 // Проблемы управления и информатики. – 2007. - №3 - С. 49 – 63. ↑

12. Панкратова Н.Д., Недашковская Н.И. Методология обработки нечеткой экспертной информации в задачах предвидения. Часть 1 // Проблемы управления и информатики. – 2007. - №2 - С. 40 – 55. ↑

13. Панкратова Н.Д., Недашковская Н.И. Методология обработки нечеткой экспертной информации в задачах предвидения. Часть 1 // Проблемы управления и информатики. – 2007. - №2 - С. 40 – 55. ↑

14. Панкратова Н.Д., Недашковская Н.И. Методология обработки нечеткой экспертной информации в задачах предвидения. Часть 1 // Проблемы управления и информатики. – 2007. - №2 - С. 40 – 55. ↑

15. Грешилов, А. А. Математические методы принятия решений: Учеб. пособие / А. А. Грешилов. - Москва: Изд-во МГТУ. 2006. – С. 112. ↑

16. Панкратова Н.Д., Недашковская Н.И. Методология обработки нечеткой экспертной информации в задачах предвидения. Часть 1 // Проблемы управления и информатики. – 2007. - №2 - С. 40 – 55. ↑

17. СППР Expert Choice // www.expertchoice.com. ↑

18. Катулев А. Н. Математические методы в системах поддержки принятия решений: Учеб пособие / А. Н. Катулев, Н. А. Северцев. — М.: Высшая школа. 2005. – С. 79. ↑

19. Ногин В. Д. Принятие решений в многокритериальной среде: количественный подход / В.Д. Ногин. - Изд. 2-е. испр. и доп. - М.: ФИЗМАТЛИТ. 2005. - С. 60. ↑

20. Катулев А. Н. Математические методы в системах поддержки принятия решений: Учеб пособие / А. Н. Катулев, Н. А. Северцев. — М.: Высшая школа. 2005. – С. 79. ↑

21. Катулев А. Н. Математические методы в системах поддержки принятия решений: Учеб пособие / А. Н. Катулев, Н. А. Северцев. — М.: Высшая школа. 2005. – С. 79. ↑

22. Грешилов, А. А. Математические методы принятия решений: Учеб. пособие / А. А. Грешилов. - Москва: Изд-во МГТУ. 2006. – С. 116. ↑

23. Составлено автором. ↑

24. Составлено автором. ↑

25. Составлено автором. ↑