Файл: Выбор управленческого решения методом анализа иерархий. Оценить корректность метода на примере конкретной организации.pdf

Рисунок 2 - Структурная схема системного подхода к оцениванию достоверности результатов ММАИ^[9]

1.3. Модифицированный метод анализа иерархий

(ММАИ) обработки нечетких экспертных оценок

Традиционный МАИ, предложенный Т. Саати, позволяет обрабатывать лишь точечные экспертные оценки. Н. Д. Панкратовой, Н. И. Недашковской разработан модифицированный МАИ, позволяющий принимать решение с учетом нечетких экспертных оценок^[10]. Представление оценок экспертов в виде нечетких чисел позволяет полнее описать экспертную информацию и тем самым повысить достоверность решений, полученных на ее основе^[11]. Дано:

- множество альтернатив решений;

- множество критериев;

- множество нечетких матриц парных сравнений альтернатив относительно критериев.

Необходимо:

• найти вектор нечетких глобальных весов , отображающий преобладания, записанные во всем множестве ;
• оценить согласованность нечеткой экспертной информации;
• определить ранжирование нечетких глобальных весов ;
• оценить степень доверия к полученному ранжированию.

ММАИ обработки нечетких экспертных оценок состоит из нескольких этапов (рис.3): формирование по ответам экспертов нечеткой матрицы парных сравнений, элементами которой являются нечеткие числа, оценивание согласованности нечетких экспертных оценок, нахождение локальных весов элементов иерархии, а потом на их основе – глобальных весов. Эти этапы реализуются путем разложения нечеткой матрицы парных сравнений по множествам уровней, и осуществляется переход к работе с интервальными матрицами парных сравнений.

Для нахождения локальных весов альтернатив по критериям решений разработан двухэтапный метод^[12]: на первом этапе вычисляются минимальные величины отклонений заданной экспертом матрицы парных сравнений от неизвестной согласованной матрицы, на втором этапе уже непосредственно вычисляются веса при найденных значениях отклонений.

Рисунок 3 - Иерархическая система задач, решаемых с помощью ММАИ обработки нечеткой экспертной информации^[13]

ММАИ использует субъективную экспертную информацию и поэтому очень важный этап представляет оценивание согласованности этой информации. Н. Д. Панкратовой, Н. И. Недашковской^[14] предложен нечеткий спектральный коэффициент согласованности, позволяющий количественно выразить уровень противоречивости в заданных экспертами нечетких оценках парных сравнений.

Допустимость уровня несогласованности экспертных оценок или необходимость организации обратной связи с экспертом определяются путем сравнения нечеткого спектрального коэффициента согласованности с введенными нечеткими порогами обнаружения и применения. Так как результирующие глобальные веса нечеткие, то их ранжирование или упорядочение требует специальных методов^[15]. В этом случае используют метод, который состоит в построении подмножеств недоминированных нечетких весов. Также введены показатели степени доверия к полученному ранжированию, позволяющие оценить степени строгого преобладания и эквивалентности нечетких весов в ранжировании^[16].

1.4. Комплексное оценивание чувствительности решения, полученного на базе МАИ

При решении многих задач выбора и ранжирования анализ чувствительности полученного с помощью МАИ решения проводится графическими методами, реализованными в СППР Expert Choice: анализ чувствительности выполнения, градиентный, динамический, 2D и разностный анализ чувствительности^[17]. В этих методах пользователь может изменять веса критериев и наблюдать на экране как в виде соответствующих графиков и диаграмм изменяются веса альтернатив. Это методы типа «что будет если». Они не являются системным подходом к проведению анализа чувствительности и позволяют лишь ответить на вопрос «каким будет решение, если вес отдельного элемента иерархии изменить на некоторую величину». Однако, эти методы довольно просты в применении и поэтому широко используются на практике.

Комплексное оценивание чувствительности результатов, полученных на базе МАИ проводится в следующие порядке:

• исследование устойчивости локальных весов элементов иерархии к возмущениям в экспертных оценках;
• оценивание на основе полученных формул расчета диапазонов изменения весов элементов иерархии, при которых изменяется результирующее ранжирование альтернатив. Это дает возможность вычислить степени критичности и чувствительности каждого элемента иерархии, найти так называемые критические элементы, относительные изменения весов которых, приводящие к изменениям ранжирования, наименьшие.

Под степенью критичности элемента иерархии понимается величина наименьшего относительного изменения веса данного элемента, приводящая к изменению порядка ранжирования альтернатив.

Чувствительность – величина, обратная к степени критичности. Меньшее значение степени критичности элемента свидетельствует о меньшем изменении его веса, достаточном для изменения порядка ранжирования альтернатив, а чувствительность этого элемента к возмущениям в экспертных оценках в данном случае будет большей^[18].

Один из основных вопросов при многокритериальном оценивании – это выбор метода синтеза локальных весов для получения единого решения по группе критериев (целей). Методы синтеза можно оценивать по появлению в них так называемого явления реверса рангов^[19].

Под реверсом рангов понимают изменение ранжирования альтернатив при добавлении или исключении альтернативы. Реверс рангов может возникнуть в каждом из этих методов. А наименьший риск появления реверса рангов характерен для метода мультипликативного синтеза^[20].

Задачи предвидения подвергаются воздействию со стороны разнообразных рисков и поэтому необходимы средства для их оценивания. Риск характеризуется следующими основными показателями: степень риска, уровень риска и ресурс допустимого риска. Природа риска в задачах принятия решений с использованием экспертных оценок обусловлена действием следующих групп факторов: риска непрогнозируемых ситуаций, вызванных ситуационной неопределенностью, форсмажорного риска и риска субъективности экспертных оценок.

Модификация BOCR МАИ позволяет оценить ситуационные и форс-мажорные риски, влияющие на выбор той или иной альтернативы при нечетких экспертных оценках. Показатели оценивания риска субъективности экспертных оценок представлены на рис.4.

Рисунок 4 - Оценивание риска субъективности экспертной информации в ММАИ^[21]

При точечных оценках экспертов показатели риска субъективности – это чувствительность критических элементов иерархии и коэффициенты согласованности. При интервальных и нечетких оценках – это интервальный и нечеткий спектральные коэффициенты согласованности и степени выполнения строгого преобладания и эквивалентности в ранжировании^[22].

Выводы

Метод анализа иерархий (МАИ) — это научно-обоснованный с позиции системного анализа подход в принятии решений для выбора альтернативы из множества возможных на основе нескольких критериев. Данный метод может использоваться для решения задач управления, в том числе задач прогнозирования и стратегического планирования. МАИ позволяет упорядочить работу лица, принимающего решение, и учесть достаточно сложную систему факторов, влияющих на выбор решения.

Системный подход к оцениванию достоверности решения, полученного МАИ, включает модифицированные МАИ обработки нечетких экспертных оценок и оценивания ситуационных рисков задачи принятия решений, комплексное оценивание чувствительности полученного решения.

Модифицированные методы анализа иерархий используются в методологии сценарного анализа на этапе качественного анализа при решении задач предвидения.

2. Практические аспекты решения задач с использованием МАИ

2.1. Моделирование сценариев решения главных проблем города Санкт-Петербурга

По результатам предварительного проведенных мозговых штурмов были выявлены главные проблемы города Санкт-Петербурга, к которым в первую очередь относятся проблемы социальной сферы, экологии, земельных ресурсов, предпринимательства, инвестиций и инноваций (рис. 5).

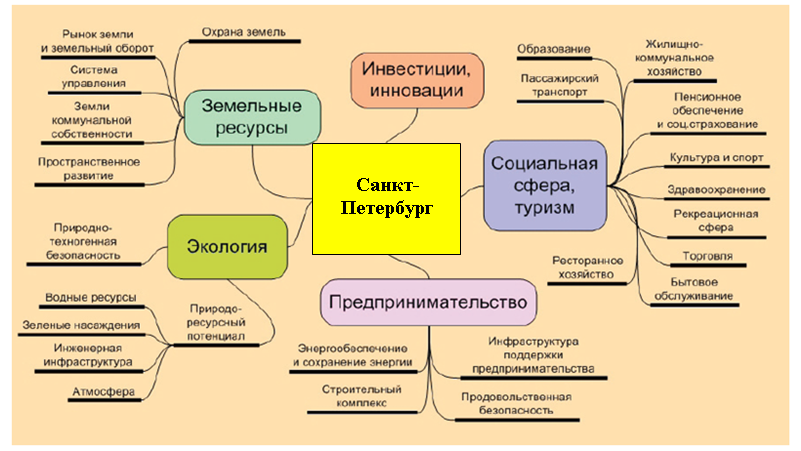
Рисунок 5 – Проблемы города Санкт-Петербурга^[23]

Для дальнейшего анализа был выбран кластер социальной сферы как наиболее проблемный для города Санкт-Петербурга. Был проведен опрос экспертов относительно путей решения проблем этого кластера и отобраны следующие проекты:

• строительство двух мусороперерабатывающих заводов;
• строительство второй нити Главного канализационного коллектора;
• строительство лечебно-диагностического корпуса городского центрального противортуберкулезного диспансера;
• реконструкция станции аэрации;
• строительство и реконструкция линий метрополитена.

Необходимо было определить коэффициенты относительных важностей этих проектов и выбрать наиболее приоритетные из них для первоочередной реализации.

Контрольные признаки доходов, затрат, ситуационных рисков и угроз, определенные по результатам экспертного оценивания методом BOCR МАИ, приведены на рис. 6.

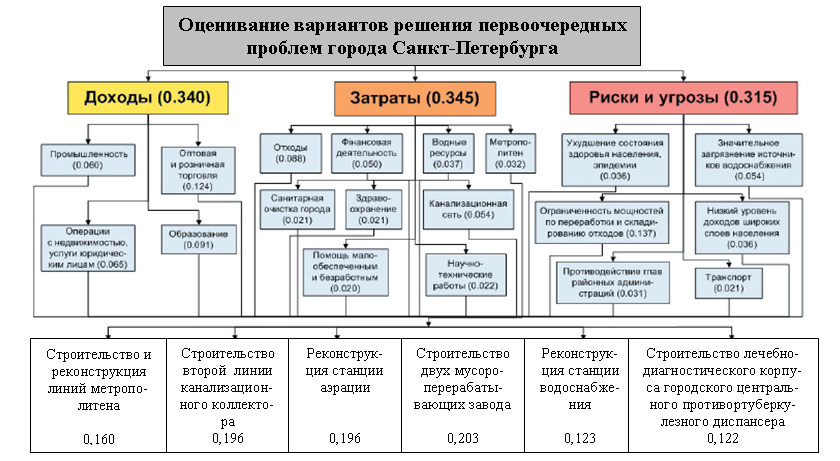
Рисунок 6 – Оценивание вариантов решения проблем города Санкт-Петербурга^[24]

На этом же рисунке указаны значения коэффициентов относительных важностей составляющих доходов, затрат и рисков, альтернативных вариантов решений. При этом, коэффициенты важностей самих групп доходов, затрат и рисков определялись МАИ путем оценивания отдельной иерархии стратегических факторов, включающей рост, стабильность и социальную ориентированность экономики, региональную безопасность и угрозы для Санкт-Петербурга. Результирующие веса проектов, формирующих последний уровень иерархии на рис. 6, позволяют сделать вывод, что первоочередными для реализации являются проекты построения двух мусороперерабатывающих заводов, второй нити Главного канализационного коллектора и реконструкция станции аэрации. Второй приоритет получили проекты строительства и реконструкции линий метрополитена. Остальные мероприятия получили третий приоритет.

2.2. Оценивание направлений рационального использования

космической информации дистанционного зонирования земли для геоинформационных систем

МАИ позволяет определить направления рационального использования космической информации дистанционного зондирования земли (ДЗЗ) при решении тематических заданий на основе геоинформационных систем (ГИС).