Файл: Информационные процессы в переработке нефти и газа.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 69
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1.Тема работы: Информационные процессы в переработке нефти и газа.
2. Исходные данные к работе: Задание 1, Вариант №2: дана таблица значений Содержание ионов Cl (X) и Плотность пластовой воды (Y).
3. Содержание пояснительной записки: титульный лист, задание, аннотация на двух языках, введение, теоретические сведения, постановка задачи, исходные данные, решение задачи в среде MS Excel,_Mathcad, заключение и список использованной литературы.
_______________________________________________________________________
4. Перечень графического материала: рисунки и графики
________________________________________________________________________
Аннотация
Пояснительная записка представляет собой отчет о выполнении курсовой работы. В ней рассматриваются вопросы по нахождению эмпирических формул методом наименьших квадратов (МНК) посредством возможностей пакета Microsoft Excel, Mathcad . В работе получены уравнения различных видов с помощью аппроксимации линейной, квадратичной и экспоненциальной зависимостей. По окончании работы сделан вывод, каким методом задача решена лучше всего.
Страниц 25, таблиц 2 , рисунков 12.
Abstract
The explanatory note represents the report on term paper performance. In it questions on a finding of empirical formulas by a method of the least squares (МНК) by means of possibilities of package Microsoft Excel, Mathcad are considered. In work the equations of various kinds by means of approximation linear, square-law and экспоненциальной dependences are received. Upon termination of work the conclusion is drawn, the problem is solved by what method is better.
Pages 25 , tables 1 figures 14 .
Содержание:
Аннотация………………………………………………………………………………….3
Введение……………………………………………………………………………………5
Постановка задачи…………………………………………………………………………5
Порядок выполнения задания…………………………………………………………….5
План решения……………………………………………………………………………...6
Исходные данные………………………………………………………………………….7
Теоретические сведения…………………………………………………………………..7
Построение эмпирических формул методом наименьших квадратов………………....7
Специальный вид линейной зависимости…………………………………………….....8
Элеметы теории корреляции…………………………………………………………..….9
Решение………………………………………………………………………………...…10
Основные выводы по решению задачи……………………………………………...….22
Заключение……………………………………………………………………………….24
Список использованной литературы…………………………………………………...25
Введение
В настоящее время большое значение придается умению использовать компьютерные технологии для выполнения расчетов различной сложности, для организации безошибочного документооборота как внутри одной фирмы, так и между различными юридическими лицами.
При решении подобных задач широко применяются офисные приложения MS Excel и MathCAD. В данной лабораторной работе на примере задач, содержащих небольшой объем исходных данных, рассматриваются основные приемы оформления документов и выполнения простых расчетов с помощью Excel, Word и MathCAD. Большое внимание уделяется обеспечению автоматического изменения результатов расчета при изменении исходных данных.
В задаче иллюстрируется составление «специализированного» и «общего» уравнения для определения содержания ионов Cl- от плотности воды, поступающей в скважину вместе с нефтью.
Постановка задачи.
Исследовать эмпирическую зависимость содержания ионов Cl- от плотности воды, поступающей в скважину вместе с нефтью.
Порядок выполнения задания
Имеются заданные таблично фактические результаты измерений и экспериментов. Требуется построить в MS Excel график таблично заданной функции, сохраняя принятые обозначения задания. Вычислить коэффициенты корреляции в MS Excel для случая линейной зависимости между исходными параметрами.
Требуется: в зависимости от вида графика и величины коэффициента корреляции, выбрать специальный вид эмпирической линейной зависимости, определив «специализированное» уравнение, уравнение «общего» вида.
Сопоставив величины коэффициентов детерминации, нужно определить, какое уравнение формально лучше описывает экспериментальные данные. Сравнить графики этих зависимостей, приведя их на рисунке.
Определить конкретный вид выбранных эмпирических функций, решив системы линейных уравнений матричным методом в MS Excel и определив значения коэффициентов. Вычислить коэффициенты детерминированности для полученных функций. Построить графики теоретических функций.
Для выбранного класса функций построить в MS Excel графики линий тренда, с выводом уравнений и коэффициентов детерминированности. Результаты вычислений сравнить
, определить, какая из полученных эмпирических формул лучшим образом аппроксимирует заданную зависимость.
План решения
1)Построить, используя МНК, и исследовать «специализированное» уравнение c(p)=c(p-1000)
2)Вычислить R12 - коэффициент детерминированности, характеризующий качество этого «специализированного» уравнения.
3)Используя МНК, построить и исследовать линейное уравнение общего вида c(p)=а2p+a1
4)Определить a1 и а2 в уравнении c(p)=а2p+a1, решив систему
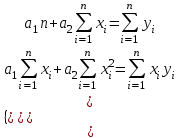
5)Вычислить R242 – коэффициент детерминированности, характеризующий качество линейного уравнения «общего» вида
6)Сравнить качество уравнений (12) и (24), сопоставив величины R12 и R22
7)Вычислить по этим уравнениям прогнозные значения величины содержанияионов Cl-, если плотность пластовой воды равна ρпрогнозн. В качестве ρпрогнозн взять величину, равную ρmax-0,1(ρmax- ρmin)/
8)Вычислить абсолютную и относительную разницу прогнозных значений.
9)Сделать вывод о целесообразности использовании этих уравнений.
Исходные данные
Таблица 1
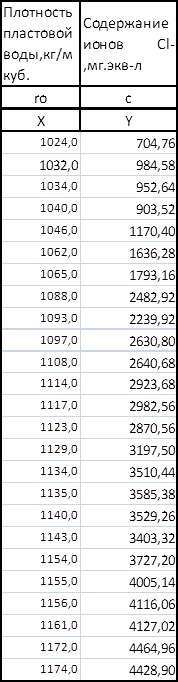
Теоретические сведения
Построение эмпирических формул методом наименьших квадратов.
Часто при анализе фактических результатов измерений или экспреримпентов возникает необходимость найти в явном виде функциональную зависимость между этими фактиескими величинами.
Для нахождения аналитической взаимосвязи между двумя величинами x и y производят ряд наблюдений; в результате плучается таблица значений.
Поскольку табличные результаты получаются как итог каких-либо экспериментов, эти значения называются эмпирическими или опытными или экспериментальными значениями. Таким образом, исходными данными являются два одномерных массива одинаковой длины, содержщие эмпирические данные.
Если между величинами x и y существует некоторая функциональная зависимость, но ее аналитический вид неизвестен, то возникает практическая задача – найти эмпирическую формулу:
 ,
,где
 - коэффициенты. Вид функции и значения коэффициентов
- коэффициенты. Вид функции и значения коэффициентов  подбираются таким образом, чтобы значения
подбираются таким образом, чтобы значения  , вычисленные по эмпириеской формуле при различных значениях xi, как можно меньше отличались бы от опытных значений yi.
, вычисленные по эмпириеской формуле при различных значениях xi, как можно меньше отличались бы от опытных значений yi.Нахождение аналитической зависимости между эмпирическими величинами называется апроксимацией фуекции, заданной таблично.
Чаще всего для аппроксимации используют метод наименьших квадратов (МНК). Каждая пара чисел (xi,yi) из исходной таблицы лпределяет точку Mi на плоскости XOY. Используя формулу
 с различными значениями коэффициентов
с различными значениями коэффициентов  , можно построить множество кривых, которые будут являться графиками теоретических функций в точке xi. Разность
, можно построить множество кривых, которые будут являться графиками теоретических функций в точке xi. Разность  называется отклонением или остатком и представляет собой расстояние по вертикали от точки Mi до графика эмпирической фнкции.
называется отклонением или остатком и представляет собой расстояние по вертикали от точки Mi до графика эмпирической фнкции.Согласно МНК, наилучшими коэффициентами
 считаются те, для которых сумма квадратов отклнений найденных теоретических значений функции от заданных эмпирических значений будет минимальной. Следовательно, задача состоит в определении коэффициентов
считаются те, для которых сумма квадратов отклнений найденных теоретических значений функции от заданных эмпирических значений будет минимальной. Следовательно, задача состоит в определении коэффициентов  таким образом, чтобы сумма квадратов отклонений была наименьшей.
таким образом, чтобы сумма квадратов отклонений была наименьшей. Специальный вид линейной зависимости.
В традиции некоторых разделов науки зависимость содержания различных ионов (минерализации) от плотности пластовой воды принято представлять в виде Y=c(X
-1000),
где X – плотность пластовой воды; Y – степень минерализации; с – некоторый параметр,зависящий от типа растворенных ионов (минералов).
Такой вид зависимости имеет ряд преимуществ по сравнению с традицонным. Во-первых, он обеспечивает нулевое значение степени минерализации для дистилированной воды, которая имеет плотность, равнуюю 1000, и при этом значении X, и, очеидно, Y равны нулю. Во-вторых, параметр с имеет простой смысл – он показывае, на сколько повышается степень минерализации для пластовой воды, если ее плотность возрастает на еденицу по сранению с плотностью дистилированной воды.
Чтобы определить коэффициент с в зависимости Y=c(X-1000), достаточно сделать замену Z= (X-1000).
Тогда зависимость Y=c(X-1000) примет вид Y=cZ.
Чтобы найти коэффициент c с помощью МНК, воспользуемся следующими соотношениями. Цель МНК – найти такое значение с, чтобы сумма квадратов отклонений
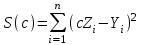 . Необходимым условием экстремума является соотношение
. Необходимым условием экстремума является соотношение  . Соотношение
. Соотношение  может быть преобразованно к виду:
может быть преобразованно к виду: 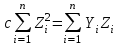 . Отсюда можно определить c:
. Отсюда можно определить c: 
Элементы теории корреляции.
График теоретической зависимости YT(x), полученный по найеденно эмпирической формуле, называется кривой регрессии. Для проверки согласия (справедливости) построенной кривой регрессии с результатами эксперимента, как правило, исользуют следущие характеристики: коэффициент корреляции и коэффииент детерминированности.
Коэффициент корреляции является мерой линейной связи между зависимыми величинами. Он показывает, насколько хорошо, в среднем, может быть представлена (вычислена) одна из величин в виде линейной функции от другой.
Коэффициент корреляции равен
 , где
, где 