Файл: Шикунова Дмитрия Алексеевича Выполнение Оформление сто 04. 012012 Устный отчет.docx
Добавлен: 11.01.2024
Просмотров: 68
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
электроны обладают меньшей диффузионной способностью, чем медленные, и ТЭДС в соответствии с этим меняет знак. Величина и знак ТЭДС зависят также от формы поверхности Ферми.
В термоэлементе, состоящем из дырочного и электронного полупроводников, ТЭДС складываются. В полупроводниках со смешанной проводимостью к холодному контакту диффундируют и электроны и дырки, и их заряды взаимно компенсируются. Если концентрации и подвижности электронов и дырок равны, то ТЭДС равна нулю.
2) Вторая (контактная) составляющая – следствие температурной зависимости контактной разности потенциалов. Если оба контакта термоэлемента находятся при одной и той же температуре, то контактная и объёмная ТЭДС исчезают. Контактная разность потенциалов – разность электрических потенциалов, возникающая между контактирующими телами в условиях термодинамического равновесия. Наиболее важно понятие к.р.п. для твёрдых проводников (металлов и полупроводников). Если два твёрдых проводника привести в соприкосновение, то между ними происходит обмен электронами, причём вначале преимущественно электроны переходят из проводника с меньшей работой выхода в проводник с большей работой выхода. В результате этого процесса проводники приобретают электрические заряды противоположных знаков, что приводит к появлению электрического поля, препятствующего дальнейшему перетеканию электронов. В конечном счёте, достигается равновесие, при котором потоки электронов в обоих направлениях становятся одинаковыми, и между проводниками устанавливается к.р.п.
Электрическое поле к.р.п. сосредоточено в проводниках вблизи границы раздела и в зазоре между проводниками. Линейные размеры этой области порядка длины экранирования, которая тем больше, чем меньше концентрация электронов проводимости в проводнике. Длина экранирования в металлах имеет атомные размеры (10-8–10-7 см), а в полупроводниках колеблется в широких пределах и может достигать величины 10-4–10-5 см.
Рассмотрим процесс образования контактной разности потенциалов металлов на основе зонной теории. На рисунке 3 показаны уровни Ферми и значения работы. Преимущественный переход электронов из металла 1 в металл 2 сопровождается изменением их потенциалов и соответствующим смещением энергетических уровней (по внешней шкале). Уровни металла 1, заряжающегося положительно, опускаются, а уровни металла 2, заряжающегося отрицательно
, поднимаются. Изменение положения энергетических уровней будет происходить до тех пор, пока условия перехода электронов из одного металла в другой не окажутся одинаковыми. Так, для электронов, находящихся на уровнях Ферми, условие равновесия выражается равенством (5):
где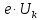
– работа, которую должен совершить электрон, идущий из металла 1 в металл 2, преодолевая к.р.п. 
.
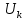Равновесное состояние между металлами иллюстрирует рисунок 4.
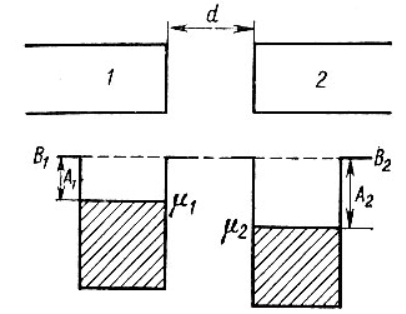
Рисунок 3 – Уровни Ферми в разных металлах
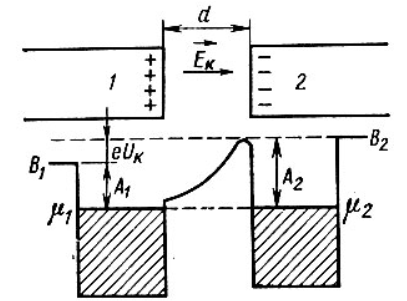
Рисунок 4 – Переход в равновесное энергетическое состояние
Если до начала перехода электронов из металла 1 в металл 2 (рисунок 3) между уровнями Ферми разных металлов имеется некоторое энергетическое расстояние, то после установления статистического равновесия эти уровни оказываются одинаковыми (по внешней энергетической шкале). Значение к.р.п. равно разности работ выхода, отнесённой к заряду электрона.
Отсюда следуют два вывода:
1) из двух соприкасающихся тел к.р.п. приходится в основном на проводники с большим сопротивлением;
2) для полупроводников в области сосредоточения к.р.п. заметно изменяется концентрация носителей заряда.
К.р.п. даже при минимально возможном зазоре создаётся за счёт перехода с контактирующей поверхности одного материала на контактирующую поверхность другого порядка пары процентов свободных поверхностных электронов (разницы между числом свободных электронов, приходящихся на 1 см2 поверхности и перешедшими электронами). Именно поэтому контактное электрическое поле оказывается локализованным в контактном зазоре и почти не захватывает объемные области металлов.
Если составить электрическую цепь из нескольких проводников, то к.р.п. между крайними проводниками определяется только их работами выхода и не зависит от промежуточных членов цепи (правило Вольта). К.р.п. может достигать величины в несколько вольт. Она зависит от строения проводника и от состояния его поверхности. Поэтому величина к.р.п. может быть изменена обработкой поверхностей (покрытиями, адсорбцией и т.п.), введением примесей (в случае полупроводников) и сплавлением с другими веществами (в случае металлов).
Пусть в полупроводнике концентрация электронов по мере удаления от внешней границы (которой на рисунке 5 соответствует координата x = 0) в глубину падает в соответствии с приведенной на этом рисунке кривой. Рассечем мысленно полупроводник в точке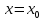
плоскостью, перпендикулярной оси Х и выделим из объёма два соседних слоя толщиной Δx. Все электроны, имевшиеся в слое 1 в некоторый начальный момент, в результате беспорядочного теплового движения через некоторое время покинут его. Поскольку вероятности движения электронов вправо и влево одинаковы, то можно считать, что половина электронов из слоя 1 перейдет через плоскость 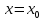. В то же самое время половина электронов из слоя 2, имеющего такую же толщину Δx, пересечет эту плоскость в обратном направлении. Поскольку средняя концентрация электронов n1 в первом слое больше средней концентрации электронов n2 в слое 2, то число электронов, пересекающих границу раздела между слоями слева направо, будет больше числа электронов, идущих навстречу. Разность между этими потоками как раз и составит тот результирующий диффузионный поток, наличие которого и определяет появление диффузионного тока.
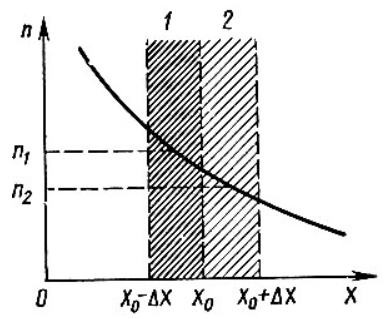
Рисунок 5 – Схематичное изображение двух слоёв полупроводника и распространения носителей заряда
Диффузионный поток будет тем больше, чем больше различие между концентрациями электронов в контактирующих слоях. Разница же между n1 и n2 определяется значением изменения концентрации электронов на единице длины в направлении, перпендикулярном границе раздела между слоями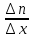
. Плотность электронного диффузионного тока можно выразить формулой (6):
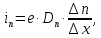
где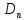
– коэффициент диффузии электронов.
Оборудование: песчаная баня, ртутный термометр, ЛАТР, термопара и мультиметр.
Ход работы:
1. Подсоединить термопару к мультиметру и опустить конец со спаем в песчаную баню;
2. включить ЛАТР и выставить значение 100;
3. нагревая до 150°C с шагом в 5°C фиксируем ЭДС на мультиметре;
4. построить градуировочную кривую ЭДС от температуры;
5. найти чувствительность термопары и построить доверительный интервал.
Результаты измерения приведены в таблице 1.
Таблица 1 – Результаты измерения
Продолжение таблицы 1
На рисунке 6 приведена градуировочная кривая.
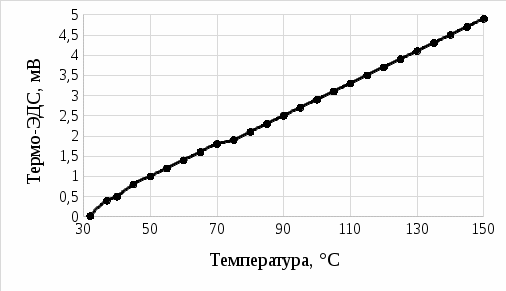
Рисунок 6 – Градуировочная кривая
На рисунке 7 представлена рассчитанная чувствительность термопары.
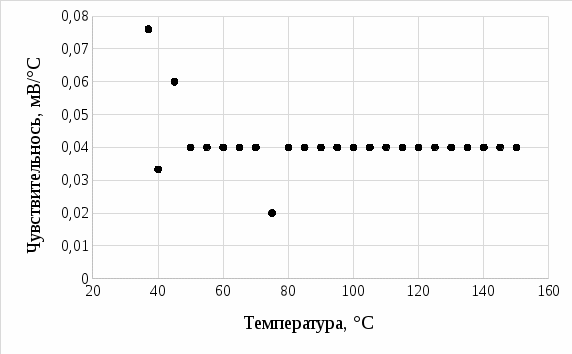
Рисунок 7 – Чувствительность термопары
Чтобы найти доверительный интервал, необходимо найти среднее значение чувствительности. Среднее значение чувствительности равно 0,041.
Рассчитаем стандартное отклонение (3):
Стандартное отклонение показывает, как распределены значения относительно среднего в выборке. Другими словами, можно понять, насколько велик разброс величины от измерения к измерению.
Доверительный уровень равен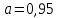
. Найдём величину 
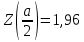согласно стандартному распределению. Нормальное распределение – распределение вероятностей, которое задаётся распределением, совпадающим с функцией Гаусса, а стандартное нормальное распределение – нормальное распределение с математическим ожиданием равным нулю и стандартным отклонением равным единице.
Найдём предел погрешности с помощью (4):
Итак, чувствительность равна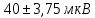
.
На рисунке 8 приведён график чувствительности термопары с доверительным интервалом.
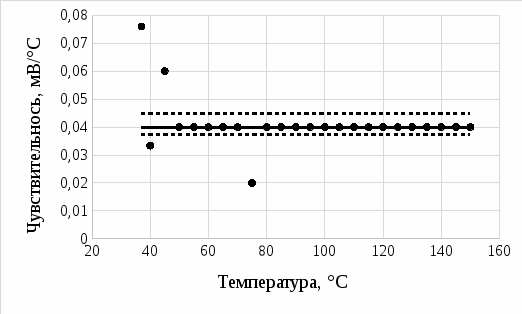
Рисунок 8 – Чувствительность термопары с доверительным интервалом
Из рисунка 8 видно, что в доверительный интервал не вошли 4 значения, что, вероятно, является ошибками оператора.
В ходе выполнения данной лабораторной работы была построена градуировочная кривая термопары по результатам измерений, рассчитан доверительный интервал, а также найдена чувствительность термопары. Чувствительность равна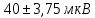
В термоэлементе, состоящем из дырочного и электронного полупроводников, ТЭДС складываются. В полупроводниках со смешанной проводимостью к холодному контакту диффундируют и электроны и дырки, и их заряды взаимно компенсируются. Если концентрации и подвижности электронов и дырок равны, то ТЭДС равна нулю.
2) Вторая (контактная) составляющая – следствие температурной зависимости контактной разности потенциалов. Если оба контакта термоэлемента находятся при одной и той же температуре, то контактная и объёмная ТЭДС исчезают. Контактная разность потенциалов – разность электрических потенциалов, возникающая между контактирующими телами в условиях термодинамического равновесия. Наиболее важно понятие к.р.п. для твёрдых проводников (металлов и полупроводников). Если два твёрдых проводника привести в соприкосновение, то между ними происходит обмен электронами, причём вначале преимущественно электроны переходят из проводника с меньшей работой выхода в проводник с большей работой выхода. В результате этого процесса проводники приобретают электрические заряды противоположных знаков, что приводит к появлению электрического поля, препятствующего дальнейшему перетеканию электронов. В конечном счёте, достигается равновесие, при котором потоки электронов в обоих направлениях становятся одинаковыми, и между проводниками устанавливается к.р.п.
Электрическое поле к.р.п. сосредоточено в проводниках вблизи границы раздела и в зазоре между проводниками. Линейные размеры этой области порядка длины экранирования, которая тем больше, чем меньше концентрация электронов проводимости в проводнике. Длина экранирования в металлах имеет атомные размеры (10-8–10-7 см), а в полупроводниках колеблется в широких пределах и может достигать величины 10-4–10-5 см.
Рассмотрим процесс образования контактной разности потенциалов металлов на основе зонной теории. На рисунке 3 показаны уровни Ферми и значения работы. Преимущественный переход электронов из металла 1 в металл 2 сопровождается изменением их потенциалов и соответствующим смещением энергетических уровней (по внешней шкале). Уровни металла 1, заряжающегося положительно, опускаются, а уровни металла 2, заряжающегося отрицательно
, поднимаются. Изменение положения энергетических уровней будет происходить до тех пор, пока условия перехода электронов из одного металла в другой не окажутся одинаковыми. Так, для электронов, находящихся на уровнях Ферми, условие равновесия выражается равенством (5):
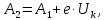 | (5) |
где
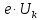– работа, которую должен совершить электрон, идущий из металла 1 в металл 2, преодолевая к.р.п. 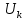.Равновесное состояние между металлами иллюстрирует рисунок 4.
Рисунок 3 – Уровни Ферми в разных металлах
Рисунок 4 – Переход в равновесное энергетическое состояние
Если до начала перехода электронов из металла 1 в металл 2 (рисунок 3) между уровнями Ферми разных металлов имеется некоторое энергетическое расстояние, то после установления статистического равновесия эти уровни оказываются одинаковыми (по внешней энергетической шкале). Значение к.р.п. равно разности работ выхода, отнесённой к заряду электрона.
Отсюда следуют два вывода:
1) из двух соприкасающихся тел к.р.п. приходится в основном на проводники с большим сопротивлением;
2) для полупроводников в области сосредоточения к.р.п. заметно изменяется концентрация носителей заряда.
К.р.п. даже при минимально возможном зазоре создаётся за счёт перехода с контактирующей поверхности одного материала на контактирующую поверхность другого порядка пары процентов свободных поверхностных электронов (разницы между числом свободных электронов, приходящихся на 1 см2 поверхности и перешедшими электронами). Именно поэтому контактное электрическое поле оказывается локализованным в контактном зазоре и почти не захватывает объемные области металлов.
Если составить электрическую цепь из нескольких проводников, то к.р.п. между крайними проводниками определяется только их работами выхода и не зависит от промежуточных членов цепи (правило Вольта). К.р.п. может достигать величины в несколько вольт. Она зависит от строения проводника и от состояния его поверхности. Поэтому величина к.р.п. может быть изменена обработкой поверхностей (покрытиями, адсорбцией и т.п.), введением примесей (в случае полупроводников) и сплавлением с другими веществами (в случае металлов).
1.4 Диффузионный ток
Пусть в полупроводнике концентрация электронов по мере удаления от внешней границы (которой на рисунке 5 соответствует координата x = 0) в глубину падает в соответствии с приведенной на этом рисунке кривой. Рассечем мысленно полупроводник в точке
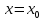плоскостью, перпендикулярной оси Х и выделим из объёма два соседних слоя толщиной Δx. Все электроны, имевшиеся в слое 1 в некоторый начальный момент, в результате беспорядочного теплового движения через некоторое время покинут его. Поскольку вероятности движения электронов вправо и влево одинаковы, то можно считать, что половина электронов из слоя 1 перейдет через плоскость 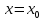. В то же самое время половина электронов из слоя 2, имеющего такую же толщину Δx, пересечет эту плоскость в обратном направлении. Поскольку средняя концентрация электронов n1 в первом слое больше средней концентрации электронов n2 в слое 2, то число электронов, пересекающих границу раздела между слоями слева направо, будет больше числа электронов, идущих навстречу. Разность между этими потоками как раз и составит тот результирующий диффузионный поток, наличие которого и определяет появление диффузионного тока. Рисунок 5 – Схематичное изображение двух слоёв полупроводника и распространения носителей заряда
Диффузионный поток будет тем больше, чем больше различие между концентрациями электронов в контактирующих слоях. Разница же между n1 и n2 определяется значением изменения концентрации электронов на единице длины в направлении, перпендикулярном границе раздела между слоями
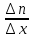. Плотность электронного диффузионного тока можно выразить формулой (6):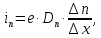 где
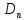– коэффициент диффузии электронов.2 Практическая часть
Оборудование: песчаная баня, ртутный термометр, ЛАТР, термопара и мультиметр.
Ход работы:
1. Подсоединить термопару к мультиметру и опустить конец со спаем в песчаную баню;
2. включить ЛАТР и выставить значение 100;
3. нагревая до 150°C с шагом в 5°C фиксируем ЭДС на мультиметре;
4. построить градуировочную кривую ЭДС от температуры;
5. найти чувствительность термопары и построить доверительный интервал.
Результаты измерения приведены в таблице 1.
Таблица 1 – Результаты измерения
| Температура, 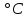 | Термо-ЭДС, 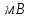 | Чувствительность,  |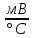
| 32 | 0,02 | |
| 37 | 0,4 | 0,076 |
| 40 | 0,5 | 0,0333 |
| 45 | 0,8 | 0,06 |
| 50 | 1 | 0,04 |
| 55 | 1,2 | 0,04 |
| 60 | 1,4 | 0,04 |
| 65 | 1,6 | 0,04 |
| 70 | 1,8 | 0,04 |
| 75 | 1,9 | 0,02 |
| 80 | 2,1 | 0,04 |
| 85 | 2,3 | 0,04 |
| 90 | 2,5 | 0,04 |
| 95 | 2,7 | 0,04 |
| 100 | 2,9 | 0,04 |
Продолжение таблицы 1
| 105 | 3,1 | 0,04 |
| 110 | 3,3 | 0,04 |
| 115 | 3,5 | 0,04 |
| 120 | 3,7 | 0,04 |
| 125 | 3,9 | 0,04 |
| 130 | 4,1 | 0,04 |
| 135 | 4,3 | 0,04 |
| 140 | 4,5 | 0,04 |
| 145 | 4,7 | 0,04 |
| 150 | 4,9 | 0,04 |
На рисунке 6 приведена градуировочная кривая.
Рисунок 6 – Градуировочная кривая
На рисунке 7 представлена рассчитанная чувствительность термопары.
Рисунок 7 – Чувствительность термопары
Чтобы найти доверительный интервал, необходимо найти среднее значение чувствительности. Среднее значение чувствительности равно 0,041.
Рассчитаем стандартное отклонение (3):
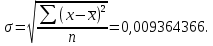 | (3) |
Стандартное отклонение показывает, как распределены значения относительно среднего в выборке. Другими словами, можно понять, насколько велик разброс величины от измерения к измерению.
Доверительный уровень равен
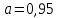. Найдём величину 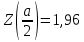согласно стандартному распределению. Нормальное распределение – распределение вероятностей, которое задаётся распределением, совпадающим с функцией Гаусса, а стандартное нормальное распределение – нормальное распределение с математическим ожиданием равным нулю и стандартным отклонением равным единице. Найдём предел погрешности с помощью (4):
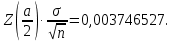 | (4) |
Итак, чувствительность равна
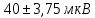.На рисунке 8 приведён график чувствительности термопары с доверительным интервалом.
Рисунок 8 – Чувствительность термопары с доверительным интервалом
Из рисунка 8 видно, что в доверительный интервал не вошли 4 значения, что, вероятно, является ошибками оператора.
ЗАКЛЮЧЕНИЕ
В ходе выполнения данной лабораторной работы была построена градуировочная кривая термопары по результатам измерений, рассчитан доверительный интервал, а также найдена чувствительность термопары. Чувствительность равна