Файл: Функции в окружающем мире.docx

Вывод

Функция-это понятие, которое развивалось одновременно с человечеством, и всегда была рядом. По началу люди не пытались как-либо систематизировать зависимости, но со времен математики, ученые начали задумываться о зависимости одной переменной от другой, и это стало огромным поводом для споров в научном мире. Первым человеком, который начал развивать тему зависимости был математик Декарт. В дальнейшем понятие функции развивалось, и получало множество новшеств, которые также стали темами для множества дискуссий, и развивается сих пор, но уже в очень медленно.

Определение функции

Определение. Числовой функцией с областью определения D называется соответствие, при котором каждому числу x из множества D сопоставляется по некоторому правилу единственное число y, зависящее от x. Принято называть x независимой переменной или аргументом, а у — зависимой переменной или значением функции.

Записывают указанное соотношение между x и у в общем виде так: у = f (x) или у = F (x) и т. п.

График функции y = f (х) - это множество всех точек плоскости, координаты (х, у) которых удовлетворяют соотношению y = f(x).

Способы задания функции:

аналитический (с помощью формулы);
графический;
табличный;
словесный.

Функции, изучаемые в школе:

линейная y = ax + b;
квадратичная y = ax² + bx + c;
обратная пропорциональность ;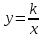
корень n- степени ;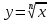
модуль y = | x |;
тригонометрические y = sinx, y = cosx, y = tgx, y = ctgx;
показательная ;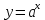
логарифмическая .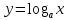

Аналитический способ

Функцию можно задать с помощью аналитического выражения (например, формулой). В этом случае её обозначают как соответствие в форме равенства.

Примеры:

Функция, заданная одной формулой:

f(x)=x+1

Графический способ

Функцию можно также задать с помощью графика. Это множество точек часто является гиперповерхностью. В частности, при {y= n=1}n=1 график функции в некоторых случаях может быть изображён кривой в двумерном пространстве.

Для функций трёх и более аргументов такое графическое представление не применимо. Однако и для таких функций можно придумать наглядное полу геометрическое представление (например, каждому значению четвёртой координаты точки сопоставить некоторый цвет на графике, как бывает на графиках комплекс

Линейная функция

Л 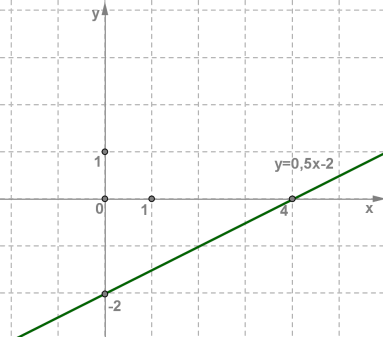инейная функция у=kx+b, графиком является прямая.

Квадратичная функция.

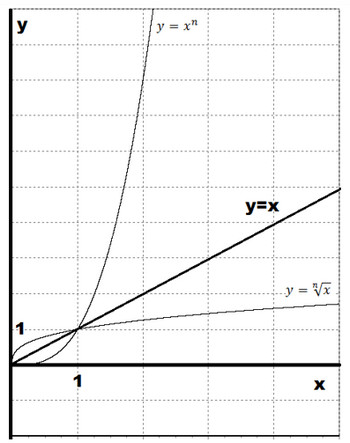
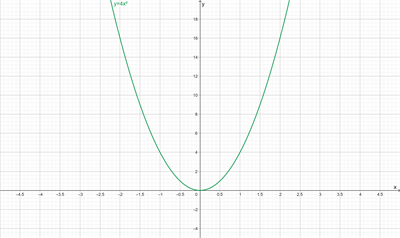
Квадратичной функцией называется функция, которую можно задать y = ax2 + bx + c, где x – переменная, a, b и c – некоторые числа, причем a ≠ 0. Изучение квадратичной функции мы начнем с частного случая, а именно с функции y = ax2. Мы уже встречались с функцией y = x2, когда a = 1. Ее графиком является парабола.

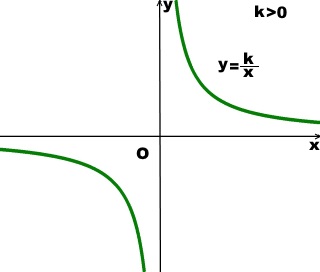
Обратная пропорциональность

При одинаковой продуктивности количество школьников, решающих конкретную задачу, обратно пропорционально времени выполнения этой задачи; количество конфет, купленных на определенную сумму денег, обратно пропорционально их цене; время на маршрут и скорость, с которой путь был пройден — обратно пропорциональные величины.

Корень n- степени из x

Корнем n-ой степени из неотрицательного числа aназывают такое неотрицательное число, при возведении которого в степень n получается число а.

Корнем нечётной степени n-ой из отрицательного числа а называют такое отрицательное число, при возведении которого в степень n получается а.

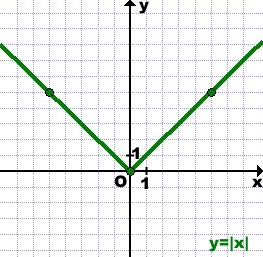
Модуль y = | x |

Проезд машины из точки А в точку Б

Соответственно, при x≥0 график модуля — прямая пропорциональность y=x, при x<0 — y= -x. То есть график функции y=|х| состоит из двух лучей — биссектрисы I и биссектрисы II координатных углов.

Тригонометрические y = sinx, y = cosx, y = tgx

y=cosx, примером является математический маятник

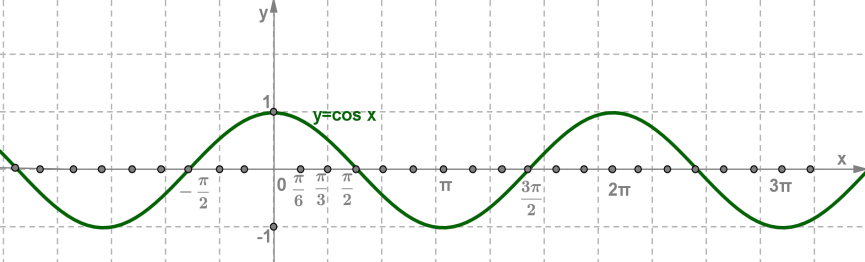
y=sinx, примером является математический маятник

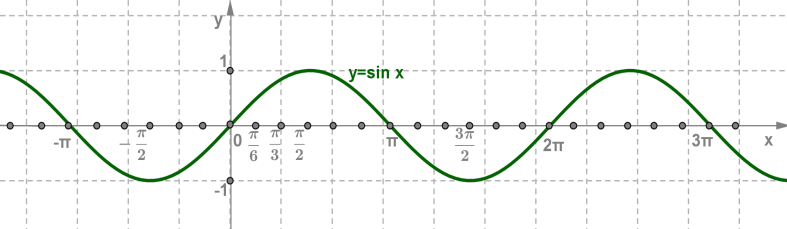
y = tgx

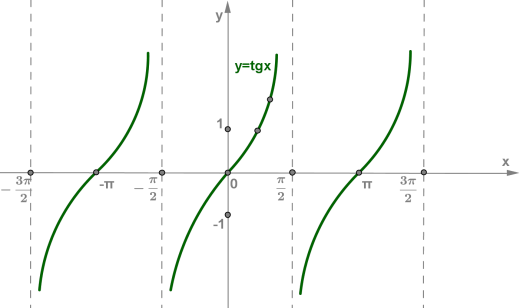
Показательная

Ф 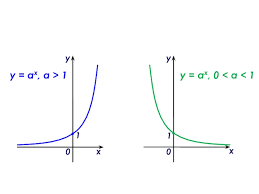ункция вида y = a x , где a — заданное число, x — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.

Логарифмическая

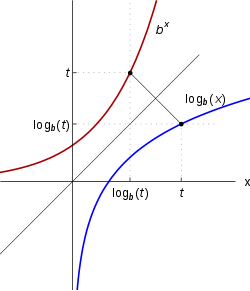
Логарифмической функцией называется функция вида y = log_ax, где a > 0 и a ≠ 1. Рассмотрим свойства функции: Областью определения функции является множество всех положительных чисел D(y) = (0; +∞). Множеством значений функции являются все действительные числа R.

Функциональные зависимости в повседневной жизни

В повседневной жизни мы постоянно сталкиваемся с функциональными зависимостями. Мы нашли множество примеров функций, которые изобразили с помощью графиков.

Пример 1. Рассмотрим деление праздничного торта между гостями. Отчего зависит количество порций? – от числа гостей. А от чего зависит вес порции? – тоже от числа гостей.

− В первом случае, чем больше гостей, тем на большее количество порций мы должны разделить торт .

З

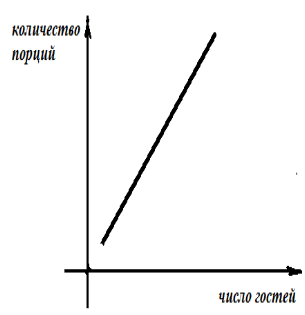
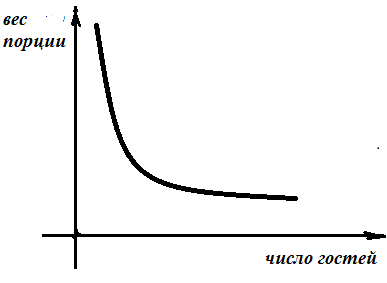
десь наглядно можно представить прямую пропорциональную зависимость.

В
Рис. 2
о втором случае, чем больше гостей, тем меньше вес порции. Здесь мы видим обратную пропорциональную зависимость.

П 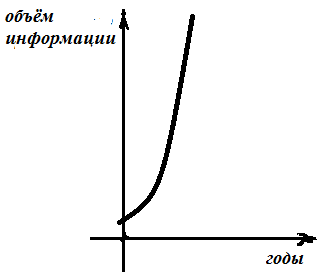ример 2. Мы живём в век информационных технологий. Ежедневно мы получаем массу информации из различных источников: телевидения, радио, газет, журналов, и, конечно, из Интернета. Известно, что объём информации каждые пять лет увеличивается в два раза.

Если построить график зависимости объёма информации от времени, то получим некоторую кривую, которая в математике называется экспонентой и является графиком показательной функции.
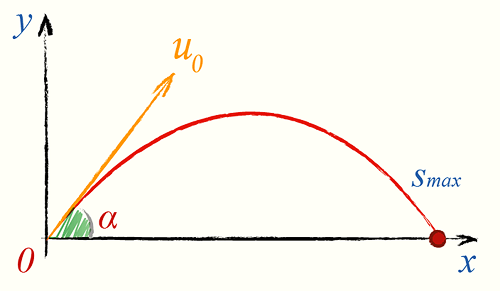
Пример 3. Траектория и скорость полёта мяча от силы, приложенной к нему (в нормальных условиях)

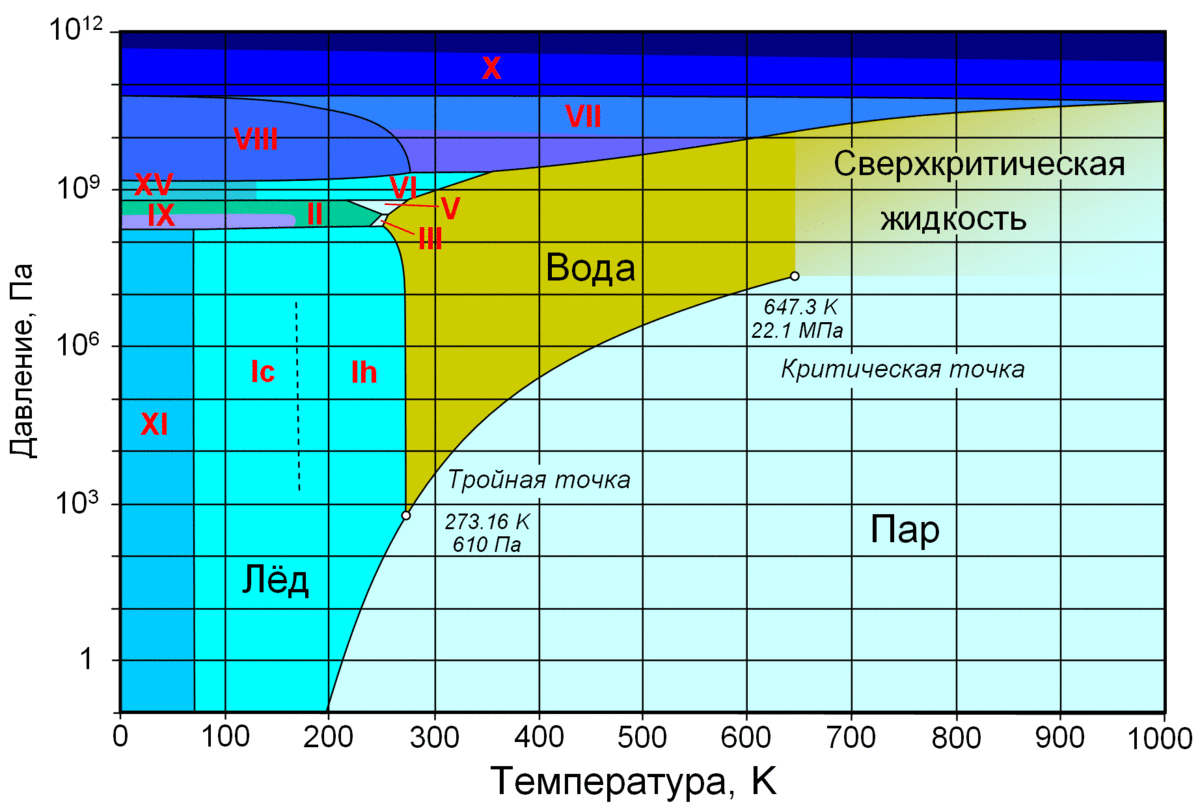
Пример 4. Состояния воды в зависимости от температуры и давления.

Максимально известная зависимость, любому человеку.

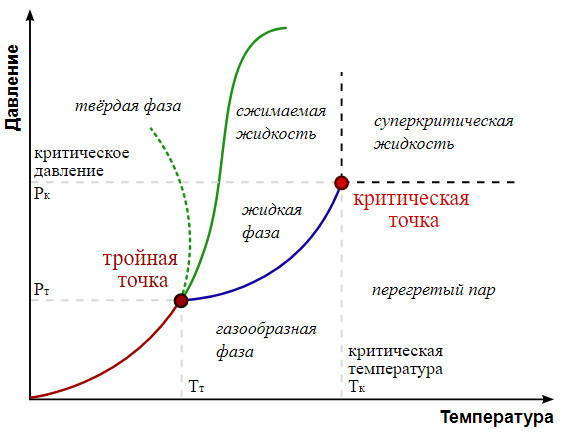
Пример 5. График зависимости от (давления и температуры) агрегатного состояния вещества.

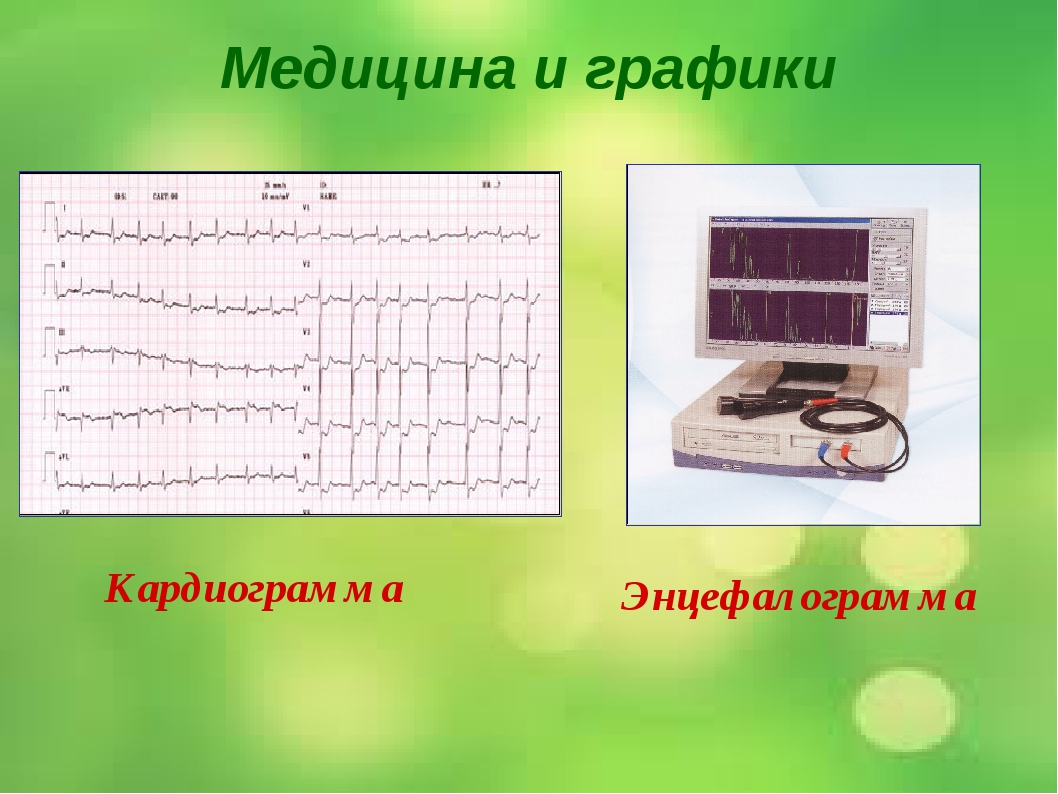
Пример 6. Медицина и графики Кардиограмма Энцефалограмма Лечением людей с сердечно-сосудистыми заболеваниями занимаются врачи-кардиологи. Проводя лечение, врач должен брать на заметку все происходящее, что поможет назначить правильные лекарственные препараты. Чтобы быть достаточно уверенным при назначении лечения врач обращается к помощи электрокардиограммы. Под кардиограммой подразумевается кривая (график), с помощью которой можно определить истинную активность сердечной мышцы. Под кардиограммой и энцефалограммой подразумевается кривая (график), с помощью которой можно определить истинную активность сердечной мышцы в кардиограмме и активность мозговой деятельности в энцефалограмме.

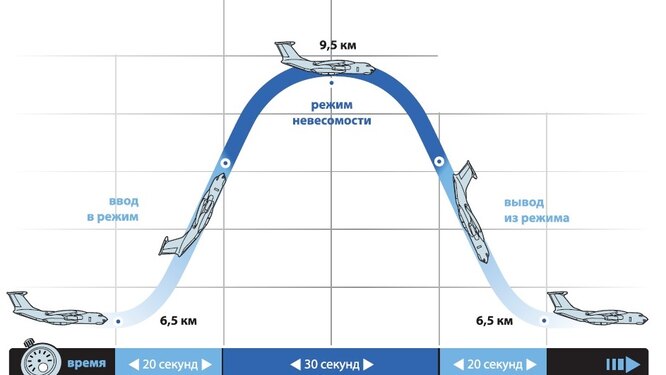
Применения в полётах на невесомость

Такая траектория называется Параболой Кеплера. Сначала самолет летит горизонтально, затем набирает высоту поднимаясь по траектории параболы

, при достижении верхней точки параболы силы тяготения и сила инерции уравниваются, и возникает невесомость.

Узнать больше о полетах в невесомость можно узнать в приложении 1

Применение в передачи информации

С

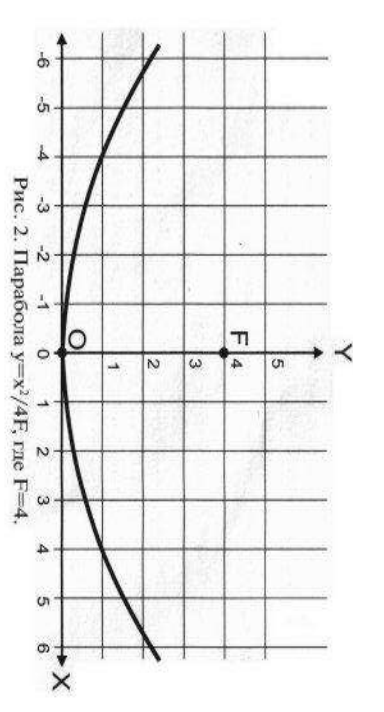войство фокуса параболы используют в телескопических антеннах

Применение в архитектуре

Под действием собственного веса и веса мостового пролёта тросы провисают и образуют дугу, близкую к параболе. Ненагруженный трос, подвешенный между двумя опорами, принимает форму т. н. «цепной линии», которая близка к параболе в почти горизонтальном участке. Если весом тросов можно пренебречь, а вес пролёта равномерно распределён по длине моста, тросы принимают форму параболы.