Файл: Лекция№11физика СТб12-2.doc

Лекция №11.

1. Уравнение Менделеева - Клапейрона.

2. Барометрическая формула.

3. Распределение Больцмана.

4. Основное уравнение М.К.Т. (уравнение Клаузиуса).

5. Средне квадротическая скорость молекул газа.

6. Средняя кинетическая энергия поступательного движения молекул газа.

7. Закон распределения молекул идеального газа по скоростям и энергиям теплового движения.

1. Уравнение Менделеева-Клапейрона.

Между параметрами определяющими состояние газа существует определенная связь, называемая уравнением состояния. Его общий вид: , где каждый из параметров является функцией 2-х других.

Объединив закон Бойля-Мариотта и Гей-Люссака, Клапейрон вывел уравнение состояния идеального газа

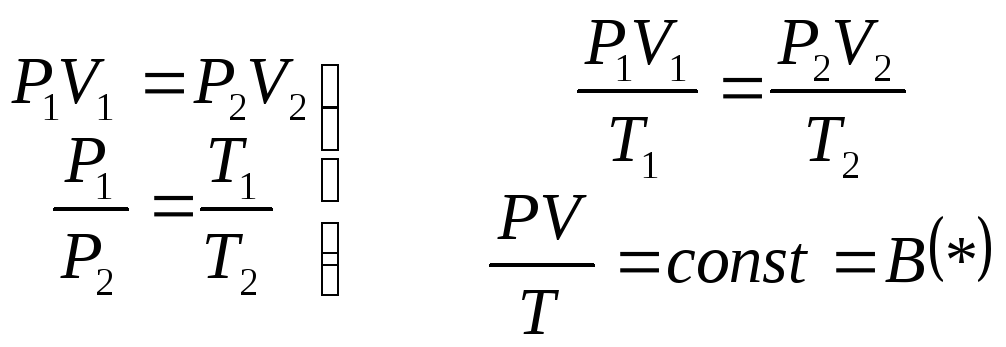(12.1)

Для данной массы газа величина постоянная, различная для различных газов.

Менделеев объединил уравнение Клапейрона с законом Авогадро отнеся уравнение (*) к 1-му молю и использовав соответственно молярный объемV_. Тогда постоянная будет одинакова для всех газов и обозначается – молекулярная газовая постоянная.(12.2)

и – давление, молярный объем и абсолютная температура газа.Физический смысл –универсальная газовая постоянная, численно равная работе совершенной 1 молем идеального газа при изобарном повышении температуры на 1С.

Определяется из уравнения (12.2) при нормальных условиях:

---

и

Для произвольной массы газа с молярной массойи объемомуравнение Менделеева-Клапейрона имеет вид:, (12.3)

так как ;, (12.4)

С учетом того что – концентрация,

, тогда ;– представляет собой универсальную газовую постоянную, отнесенную к 1 молекуле.

Тогда (12.5)

Давление идеального газа при данной прямо пропорционально концентрации его молекул. Из 12.5 , то есть, при одинаковыхивсе газы содержат в единице объема одинаковое число молекул.

Число молекул содержащихся в газа при нормальных условиях называетсячислом Лошмидта. .

Уравнение Менделеева-Клайперона является обобщением экспериментальных газовых законов и включает их в качестве частных случаев.

2. Барометрическая формула.

Из-за хаотичного теплового движения молекулы газа занимают весь предоставленный объем, равномерно заполняя его, в случае, если на молекулы газа не действуют внешние силы. Атмосферный воздух земли не ограничен стенками, но не разлетается – этому препятствует сила земного притяжения.

---

С другой стороны при отсутствии теплового движения () каждая отдельная молекула газа должна была бы падать вниз – они скопились бы у поверхности земли, где их потенциальная энергия минимальна.

Благодаря борьбе этих двух противоположных тенденций установлено подвижное равновесие, при котором – концентрация молекул воздуха у поверхности земли максимальна и постепенно уменьшается с высотой.

Так как , следовательно, по мере подъема над уровнем земли и уменьшением концентрации будет так же уменьшаться и атмосферное давление.

Зависимость давления от высоты р(h) – называется Барометрической формулой: (12.6)

Отсчет высоты идет от уровня моря, где считается нормальным, поэтому можно записать(12.7)

По этой формуле можно определить атмосферное давление в зависимости от высоты, или, измерив, давление, найти высоту.

–молярная масса;

–ускорение свободного падения;

–универсальная газовая постоянная;

–абсолютная температура;

–нормальное давление.

Из (12.5) следует, что давление с высотой убывает тем быстрее, чем тяжелее газ.

График зависимости:

	Определим высоту, на которой давле
	ние газа падает вдвое h1/2)=1/20.Подставим это в (12.7) и получим ; для воздуха М=29, и
	то есть при подъеме на высоту 6 км
	над уровнем моря, падает до
	половины от первоначального значе-
	ния. При подъеме на 12 км давление
	упадет до первоначального и т.д.

---

Измеряя барометром давления в горах можно согласно формуле (12.7) определить высоту места над уровнем моря. На этом принципе основаны устройства авиационных высотомеров - альтиметров.

---

3. Распределение Больцмана.

Поскольку давление Р прямопропорционально концентрации n, то для зависимости концентрации газовых молекул от высоты получается аналогичная формула. 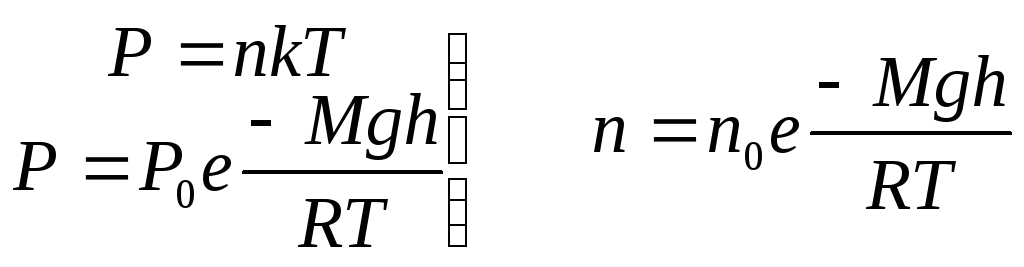(12.8)

n - концентрация на высоте h; – концентрация на высоте

–молярная масса молекулы; - универ. газовая постоянная

…(12.9)

где – представляет собой потенциальную энергию на высоте h

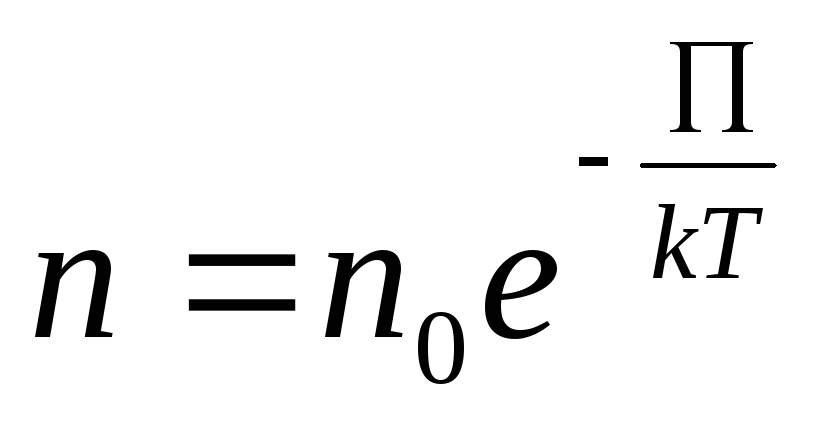……….(12.10)

Изменение концентрации молекул с высотой зависит от соотношения между энергией теплового движения и потенциальной энергией молекул на данной высоте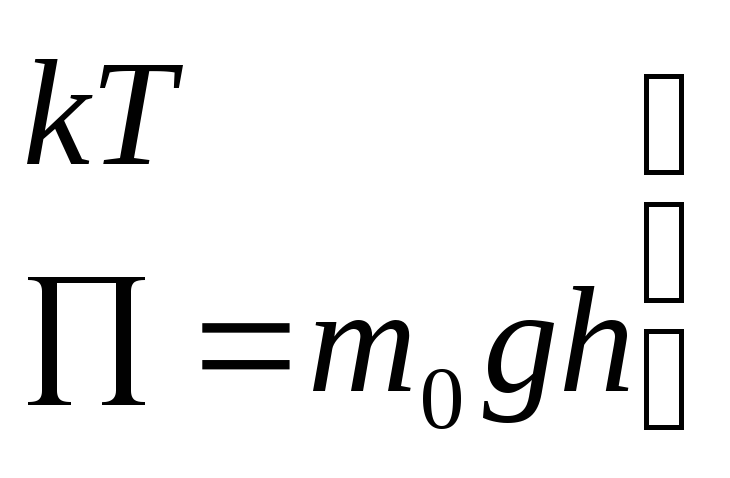

Больцман показал, что соотношение (12.10) остается справедливым в самом общем случае при наличии любых внешних сил, а не только в поле тяжести. Поэтому (12.9) и (12.10) носит название распределение Больцмана.

4. Основное уравнение мкт.

Основным уравнением кинетической теории газов принято называть уравнение устанавливающее связь между давлением газа, его объемом и энергией. Сила давления газа на стенку сосуда складывается из взаимодействий многочисленных молекул всё время ударяющихся об эту стенку и отскакивающих обратно.

Основное уравнение выводится для идеального газа. Идеальный газ подчиняется уравнению Менделеева - Клапейрона 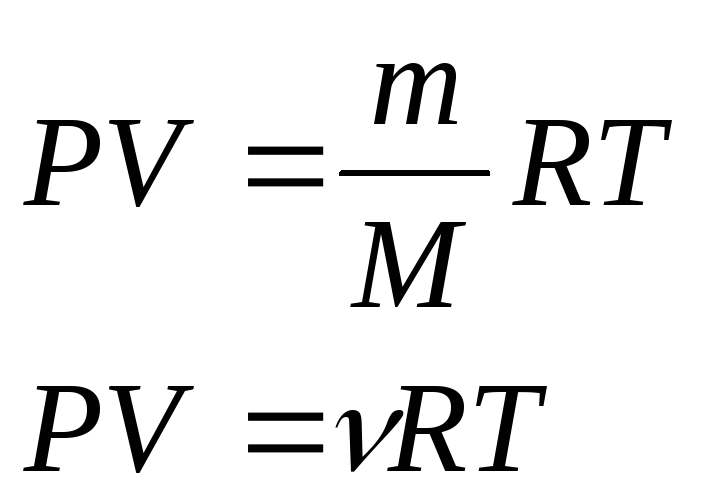. Это справедливо, если межмолекулярные расстояния таковы, что потенциальной энергией взаимодействия между молекулами можно пренебречь. Чем меньше эта энергия взаимодействия между молекулами, тем лучше удовлетворяет газ уравнению Менделеева-Клапейрона, тем ближе он по своим свойствам к идеальному. Полная энергия идеального газа сводится, следовательно, к сумме кинетической энергии всех его молекул.

---