Файл: лекции по планирован.эксперименту.doc

Лекции по курсу «Планирование эксперимента» предназначены для студентов специальности 100400 «Электроснабжение промышленных предприятий», обучающихся на 4 курсе.

Задачей курса «Планирование эксперимента» является ознакомление студентов с основными понятиями и методами планирования эксперимента как в лабораторных, так и в производственных условиях, обучение студентов применению полученных знаний в научно-исследовательской работе как в пределах вуза, так и в дальнейшей производственной деятельности.

Для успешного овладения материалом курса «Планирование эксперимента необходимо знание дисциплин «Высшая математика», «Математические задачи в электроэнергетике», «Основы метрологии». Требуется знание понятия и свойств непрерывных функций многих переменных, дифференциального исчисления, разложения функций в степенные ряды, поведение функций и построение графиков, свойства поверхностей второго порядка, свойства матриц, вычисление и анализ определителей, понятие вероятности и её свойства, определение точечных и интервальных оценок случайных величин, проверка статистических ошибок, понятие погрешности и точности измерений и т.д.

По учебному плану СКГМИ (ГТУ) по курсу «Планирование эксперимента» предусмотрен зачет в 7-м семестре.

Составители: д.т.н., проф. Васильев И.Е.

к.т.н., ст. преп. Клюев Р.В.

Введение

1. Основы теории инженерного эксперимента

1.1. Эксперимент как объект исследования

«... Теория - это хорошая вещь,

но правильный эксперимент

остается навсегда» (П. Капица)

Для инженерных исследований характерно органическое сочетание аналитического и экспериментального методов изучения явлений и процессов. Обычно эксперимент осуществляется на основании некой теории, определяющей постановку задачи и интерпретацию результатов эксперимента. Наибольшее распространение в области электроэнергетики получили измерительные эксперименты, выявляющие количественные характеристики исследуемых объектов. Они делятся на пассивные и активные. В пассивных экспериментах ведется наблюдение за процессами без вмешательства человека в его протекание. В активных - ставятся опыты, предусматривающие определенную последовательность изменения человеком влияющих факторов. Эксперименты проводятся либо на натурных объектах, либо на моделях, в том числе математических, сохраняющих особенности натурных объектов. Результаты эксперимента обрабатываются с использованием методов математической статистики и интерпретируются на основе теоретических представлений. Упрощенная схема типичного измерительного эксперимента представлена на рис. 1.1.

Из рис. 1.1. следует, что инженерный эксперимент базируется на теории обработки результатов наблюдения теории планирования экспериментов, которая является сравнительно молодой и интенсивно развивается. Основное требование к результатам эксперимента - их воспроизводимость, т.е. получение качественно совпадающих результатов при повторении экспериментов другими экспериментаторами на других установках.

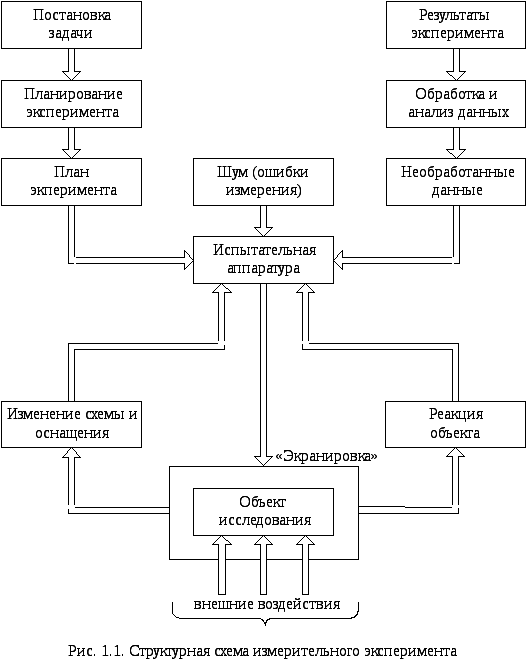
Следует отметить, что точность испытательной аппаратуры всегда ограничена и должна соответствовать необходимой точности результатов эксперимента, которая не может быть выше точности испытательной аппаратуры. Конечным результатом исследования является построение регрессионной математической модели, погрешность которой должна задаваться исследователем в зависимости от характера решаемой задачи.

Для анализа уровней напряжения, изменение которого не превышает 10% (2,54), для модели может принята погрешность не более погрешности измерительных приборов, т.е. 1-2%.

При анализе потерь активной мощности значение потерь электроэнергии, выраженное в процентах, должно округляться таким образом, чтобы число содержало не более одного знака после запятой. Это означает, что если потери электроэнергии в питающих сетях составляют 5% суммарной выработки, то, для того чтобы гарантировать точность первой цифры после запятой, необходимо иметь модель с точностью Таким образом, для целей анализа потерь электроэнергии и оценки эффективности проводимых мероприятий по снижению потерь, модель должна иметь погрешность не более 1-2%.

В сопоставительном анализе потерь мощности погрешность может быть выше, примерно, 5%. Для определения потерь реактивной мощности и токов короткого замыкания модель может допускать погрешность 10%.

Планирование эксперимента - это процедура выбора числа и условий постановки опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью, методов математической обработки их результатов и принятия решения.

Метод планирования экспериментов (МПЭ) для получения уравнений регрессии отличается от обычной процедуры метода наименьших квадратов (МНК) организованностью экспериментов (расчетов), которые проводятся в определенных точках и в требуемых количествах, возможностью использования некоторых критериев оптимальности при построении экспериментальных планов, значительным снижением трудоемкости расчета коэффициентов уравнения регрессии для случая ортогонального планирования.

Чаще всего эксперимент ставят для решения одной из двух основных задач. Первую задачу называют экстремальной. Она заключается в отыскании условий процесса, обеспечивающих получение оптимального значения выбранного параметра. Признаком экстремальных задач является требование поиска экстремума некоторой функции. Эксперименты, которые ставят для решения задач оптимизации, называют экстремальными.

Вторую задачу называют интерполяционной. Она состоит в построении интерполяционной формулы для предсказания значений изучаемого параметра, зависящего от ряда факторов. Для решения любой задачи необходимо иметь математическую модель объекта исследования. Под моделью понимают вид функции отклика (зависимости) y=f(x₁, x₂,...., x_n), где x₁, x₂,...., x_n- независимые переменные, у - зависящая от них величина. Между у и x_i связь может быть различной (функциональная, стохастическая или корреляционная). Она выражается в том, что на изменения одной величины другая случайная величина реагирует изменением своего математического ожидания или среднего значения (среднего), а также связь случайной величины с величинами неслучайными. Решение задачи осуществляется на основе регрессионного анализа.

1.2. Основы теории обработки результатов эксперимента

Обработка данных эксперимента имеет своей целью представление его результатов в наглядной форме при обязательной оценке погрешности результата.

Существует три основных видов ошибок: систематические, случайные и грубые ошибки. Первые обычно исключаются путем калибровки приборов по эталонам и не рассматриваются. Случайные ошибки происходят от различных случайных причин (неконтролируемых), грубые ошибки - в результате просчета экспериментатора. Результаты измерений с грубыми ошибками значительно, иногда на порядок и выше, отличаются от других результатов измерений, и видны, как говорится, «на глаз». Теория ошибок занимается изучением случайных и грубых ошибок.

Анализ случайных ошибок

Пусть в измерительном эксперименте в результате независимых и равноточных измерений «постоянной» величины а получены значения х₁, х₂,..., х_n. Разности:

(1)

называют истинными ошибками и рассматриваются как случайные величины. При этом независимость измерений понимается как взаимная независимость случайных величин (парный коэффициент корреляции ), равноточность - как подчинение величин одному нормальному закону распределения (наиболее частый случай), с математическим ожиданием .

В качестве оценки неизвестной величины а принимают среднее изN результатов измерений:

(2)

Кажущиеся ошибки разности:

(3)

Оценка дисперсии (несмещенная):

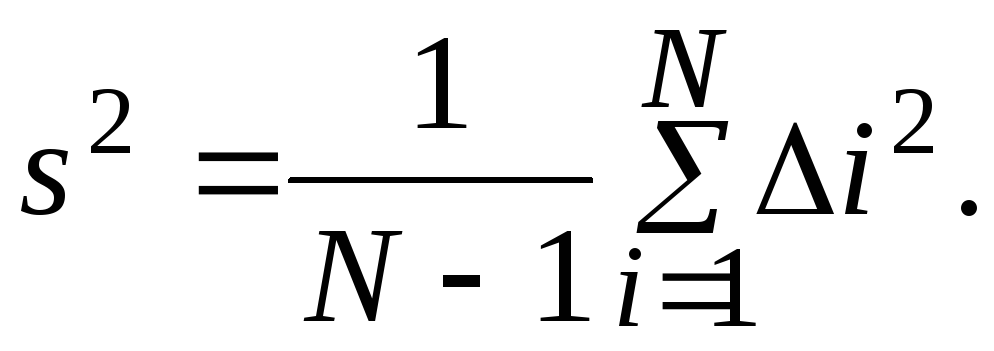(4)

Статистическая оценка, стандарт (среднее квадратическое отклонение):

(5)

Мера точности случайной величины h:

(6)

Если каждое из измерений имеет меру точностиh(x), то для среднего значения получаем меру точности:

(7)

Из (7) следует, что на повышение точности результата эксперимента наибольшее влияние оказывает повышение точности отдельных измеренийh(x) или снижение меры разброса возможных значений соответствующей случайной величины относительно среднего значения (математического ожидания).

При нормальном законе распределения случайной ошибки, точечные ошибки основаны на известном положении теории вероятности, что отношение:

(8)

подчиняется распределению Стьюдента, а отношение:

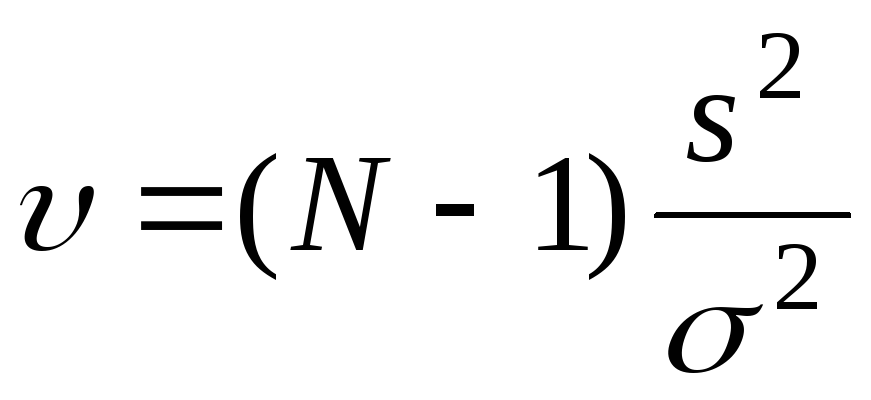(9)

подчиняется распределению (Пирсона) со степенями свободы

Точечные оценки параметров не дают информации о степени близости оценки к соответствующему теоретическому параметру. Поэтому более информативным является способ оценивания неизвестных параметров некоторым интервалом, в котором с заданной степенью достоверности окажется и оцениваемый параметр (в частностиили).

Интервальная оценка параметра , границы которогои являются функциями выборочных значений х₁, х₂,..., х_n и который с заданной вероятностью р накрывает оцениваемый параметр :