Файл: Методичка по метрологии.doc

Среднее арифметическое значение измерений = 7,971 мм. Систематическая составляющая погрешности измерения (учтенная) равна нулю. Случайная составляющая погрешности измерения

,

по таблице 1 для n = 4, n – 1 = 3 (число степеней свободы) и P = 0,95, t₀ = 3,182,

мм.

Так как в данном случае микрометр не аттестован, а известен лишь его класс, систематическая погрешность измерения переходит в разряд случайных и должна быть учтена по известному пределу допускаемой погрешности средства измерения мм.

Если величина _сл. сравнима с абсолютным значением погрешности СИ, то величину _СИ считают неисключенной систематической составляющей и в качестве доверительного интервала вычисляют величину

мм.

Измеренный диаметр вала d = 7,971 ± 0,008 мм, P = 0,95.

Оборудование и инструмент: микрометр первого класса с ценой деления 0,01 мм, набор деталей.

Задание к п. 3.1

Определить MX и выполнить поверку для микрометрического средства измерения.

Порядок выполнения работы

3.1. Поверка микрометра гладкого (МК)

3.1.1. Определение погрешности эталона.

Для поверки МК используется эталон более высокого разряда. Для выбора эталона определяется величина его погрешности. Если поправка на точность эталона не вводится, то соотношение погрешностей эталона СИэ и поверяемого МК составляет 1:5.

Для микрометров 1 класса точности Δ_СИ ± 0,004; Δ_ИЗМ ± 0,007. Для эталона погрешность должна составлять Δ_СИ = Δ_ИЗМ ≈ ± 0,0005 (± 0,5 мкм). С такой погрешностью изготавливаются концевые меры 3 класса точности.

3.1.2. Из набора концевых мер выбрать 1 меру (т.к. при большем количестве следует произвести суммирование погрешностей концевых мер по правилу:

3.1.3. Произвести замер, данные занести в таблицу.

3.1.4. Определить абсолютную ошибку СИ как разность между показаниями СИ(х) и эталона (х_д), данные занести в таблицу:

Δ = х – х_Д.

Примечание: в таблице указать знак погрешности

3.1.5. Сделать вывод о пригодности СИ к эксплуатации.

3.1.6. Сделать вывод: каким методом поверки пользовались при аттестации МК.

Задание к п. 3.2

3.2. Изучить методические указания.

3.3. Измерить деталь микрометром. Провести не меньше 5 замеров в одной точке.

3.4. Определить среднее значение измерения .

3.5. Определить отклонение результатов замеров от среднего значения и занести в таблицу.

3.6. Проверить результаты измерений на отсутствие грубых ошибок. При их наличии измерение считать грубым и отбросить.

3.7. Определить среднее квадратичное отклонение по формуле:

.

3.8. Определить случайную составляющую погрешности измерения для Р = 0,95 по формуле:

.

3.9. Исключить систематическую погрешность, (∆_изм.с. = , см. в п. 3.1).

3.10. Записать полученный результат в виде: ;Р = 0,95.

Контрольные вопросы

1. MX средств измерений.

2. Основная и дополнительные ошибки СИ.

3. Систематическая и случайная ошибки СИ.

4. Как может быть задана абсолютная погрешность СИ.

5. Относительная, приведенная погрешность СИ.

6. Поверка СИ.

7. Методы поверки СИ.

8. Соотношение погрешность поверяемого СИ и эталонного СИэ.

9. Что показывают измерения деталей:

• в одной точке;

• по всей длине детали;

• в партии.

10. Какими методами исключается систематическая составляющая погрешности измерения?

11. Какой статистический параметр характеризует случайную составляющую погрешности измерений?

12. От чего зависит точность и воспроизводимость результатов измерений?

13. Что такое доверительный интервал и доверительная вероятность?

14. Как определяется случайная составляющая погрешности измерения?

15. Как записывается результат измерения?

16. Как учитываются систематические погрешности измерения, перешедшие в разряд случайных?

Лабораторная работа № 4 Нормирование и измерение шероховатости поверхностей деталей машин

Цель работы: научиться нормировать и измерять шероховатость поверхностей деталей машин.

Общие сведения

Шероховатость поверхности возникает вследствие воздействия инструмента на поверхность детали при обработке. Шероховатостью поверхности называется совокупность неровностей поверхности с относительно малыми шагами. Шероховатость измеряют на базовой длине относительно базовой линии. Обычно за базовую линию принимают среднюю линию профиля шероховатости. Средняя линия проводится так, что в пределах базовой линии среднее квадратичное отклонение профиля до этой линии минимально (рис. 1). Числовые значения базовой длины выбирают из ряда: 0,01; 0,03; 0,08; 0,25; 0,80; 2,5; 8; 25 мм.

Для точной оценки шероховатости измерения следует повторять несколько раз в разных местах поверхности и за результат принимать среднее арифметическое всех результатов измерения.

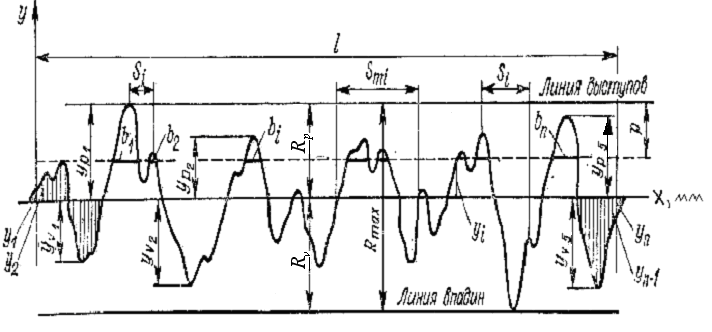
Рис. 1. Профилограмма шероховатости

Согласно ГОСТ 2789-73 шероховатость поверхности можно оценивать одним или несколькими параметрами:

или ,

где Rа – среднее арифметическое отклонение профиля; n – число выбранных точек на базовой длине; у_i – расстояние между точками профиля и средней линией; l – базовая длина; х_i – координата по оси х.

Высота неровностей по десяти точкам Rz – сумма средних абсолютных значений высоты пяти наибольших выступов профиля и глубин пяти наибольших впадин профиля в пределах базовой длины:

,

где у_рi – высота i наибольшего выступа профиля; у_vi – глубина i наибольшей впадины профиля в пределах базовой длины.

Наибольшая высота неровностей профиля R_max – расстояние между линией выступов и линией впадин профиля в пределах базовой длины:

,

где R_p – максимальная высота выступов; R_v – максимальная глубина впадин.

Средний шаг неровностей S_m: