ВУЗ: Московский технический университет связи и информатики
Категория: Учебное пособие
Дисциплина: Программирование
Добавлен: 23.10.2018
Просмотров: 5565
Скачиваний: 69
СОДЕРЖАНИЕ
Раздел 1. Основы работы с математическим пакетом Matlab
Тема 1.1. Элементы рабочей среды Matlab
1.1.1.Элементы рабочей среды Matlab и простейшие вычисления
1.1.2. Основные объекты системы Matlab
1.1.3. Лабораторная работа по теме «Элементы рабочей среды Matlab и простейшие вычисления»
1.2.2. Построение графиков и визуализация вычислений в системе MatLab
1.2.3. Лабораторная работа по теме
«Векторы, матрицы и построение графиков
1.2.4. Контрольные вопросы по теме
Тема 1.3. Средства Matlab для создания и описания m-файлов
Пример 1.3.5-1. Даны n чисел . Требуется вычислить их сумму: где
1.3.6. Лабораторная работа по теме
«Средства алгоритмизации и программирования
1.3.7. Контрольные вопросы по теме
Раздел 2. Технология решения вычислительных задач средствами MatLab
Тема 2.1. Решение нелинейных уравнений
2.1.2. Лабораторная работа по теме
«Технология решения нелинейных уравнений средствами пакета MatLab»
1. Вопросы, подлежащие изучению
2.1.3. Контрольные вопросы по теме
Тема 2.2. Технология аппроксимации интерполяции функций в среде пакета MatLab
Рис. 2.2.1-5. Вычисление функции в точке х=0.58
Рис. 2.2.2-7. Графики интерполирующих функций
Тема 2.4. Технология решения обыкновенных дифференциальных уравнений
Рис. 2.4.1-2. Решение ОДУ методом Рунге-Кутты четвертого порядка
1. Вопросы, подлежащие изучению
Тема 2.5. Технология решения задач одномерной оптимизации
2.5.2. Лабораторная работа по теме
«Технология решения задач одномерной оптимизации»
1. Вопросы, подлежащие изучению
3. Варианты индивидуальных заданий
2.5.3. Контрольные вопросы по теме
Тема 2.6. Технология решения задач многомерной оптимизации
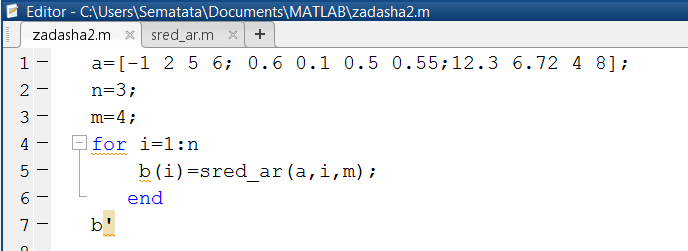
На рис. 1.3.5-4 приведен script-файл с именем zadasha2, где введена матрица, а, состоящая из трех строк и четырех столбцов. Организован цикл по количеству формируемых элементов массива b путем обращения к функции sred_ar(). В функцию передается массив а, номер строки (i) и количество элементов в строке (m). Вывод элементов массива b предусмотрен в столбец.
|
|
Рис. 1.3.5-4. Программа формирования массива b
Функция sred_ar() (рис. 1.3.5-5) предназначена для формирования i-го элемента массива b, равного среднему арифметическому элементов строки массива а.
|
|
Рис.
1.3.5-5. Функция
sred_ar(),
вычисляющая среднее арифметическое
элементов строки массива a
В результате запуска script-файле с именем zadasha2 в окно Command Window выводится столбец элементов массива b
|
|
Рис. 1.3.5-6. Запуск script-файла zadasha2
Пример.
1.3.5-3. Задать действительные числа a,b,
натуральное n
(a<b)
и вычислить выражение
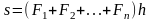 ,
где
,
где
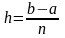 ,
если
,
если
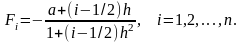
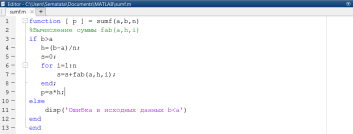
Решение задачи требует разработки двух функций: fab(a, h, i), предназначенной для вычисления i-го слагаемого (рис. 1.3.5-7) и sumf(a, h, n), предназначенной для вычисления заданного выражения (рис. 1.3.5-8).
|
|
Рис. 1.3.5-7. Функция fab(), вычисляющая значение i-го слагаемого
|
|
Рис. 1.3.5-8. Функция sumf(), вычисляющая заданное выражение
Запуск на выполнение осуществляется из командного окна к функции sumf(). Предварительно переменным a,b и n присваиваются числовые значения. Проверка правильности ввода исходных данных предусмотрена в функции sumf(). Вычисления выполняются, и результат выводится на экран только в случае, если b>a, иначе в командной строке появляется сообщение «Ошибка в исходных данных b<a» (рис. 1.3.5-9).
|
|
Рис. 1.3.5-9. Запуск функции sumf() на выполнение
1.3.6. Лабораторная работа по теме
«Средства алгоритмизации и программирования
в Matlab»
-
Вопросы, подлежащие изучению
-
Виды m-файлов.
-
Создание и сохранение новых, и открытие ранее созданных m-файлов.
-
Особенности script-файлов и m-функций.
-
Запуск на выполнение script-файла из текстового редактора.
-
Запуск на выполнение script-файла из командного окна.
-
Обращения к script-файлам и m-функциям.
-
Средства языка программирования в системе Matlab.
-
Основные операторы m-языка их назначение и форматы.
-
Общее задание
-
Изучите материал Темы 1.3 (п.п. 1.3.1 – 1.3.5).
-
Выберите индивидуальное задание из табл. 1.3.6-1.
-
Разработайте m-функции для реализации стандартных алгоритмов: вычисления конечных сумм, разветвлений, поиска минимума и максимума в последовательности данных и т.п.
-
Введите и сохраните m-функции на внешнем носителе.
-
Создайте новый script-файл, в который введите код программы, описывающий логику решения поставленной задачи.
-
Сохраните script-файл в текущем каталоге.
-
Произведите отладку script-файла, запуская его на выполнение из текстового редактора командой Run.
-
Подготовьте и введите исходные данные для решения поставленной задачи;
-
Выполните script-файл из командной строки окна Command Window.
-
Сохраните текст рабочего окна на внешнем носителе.
-
Предоставьте результаты работы преподавателю, ответьте на поставленные вопросы.
-
Выполните команду clear all для очистки Рабочей среды.
-
Оформите отчет по выполненной работе.
-
Варианты индивидуальных заданий
Таблица 1.3.6-1

-
Содержание отчета
-
В форме комментариев:
-
Название лабораторной работы
-
ФИО студента, номер группы
-
№ варианта
-
Индивидуальное задание
-
Протокол вычислений (сессии) в окне Command Window, снабженный необходимыми комментариями.
1.3.7. Контрольные вопросы по теме
-
Что такое script-файл и каковы его особенности?
-
Каким образом script-файл запускается на выполнение?
-
Что такое m-функция?
-
В чем отличие script-файла от m-функции?
-
Может ли m-функция иметь несколько выходных параметров?
-
Обращение к m-функции.
-
Формат оператора input().
-
Как с использованием оператора if…end реализовать стандартное, усеченное и вложенное разветвление?
-
Формат оператора множественного разветвления switch.
-
Формат оператора регулярного цикла for…end, особенности задания значений переменной цикла.
-
Назначение операторов continue и brek.
-
Оператор итеративного цикла while…end и его структура.
Раздел 2. Технология
решения
вычислительных задач
средствами MatLab
Тема 2.1. Решение нелинейных уравнений
2.1.1. Численное решение нелинейных уравнений
2.1.2. Лабораторная работа по теме
2.1.3. Контрольные вопросы по теме
2.1.1. Численное решение нелинейных уравнений
В общем виде уравнение можно представить, как f(x) = 0. В зависимости от вида функции f(x) различают алгебраические и трансцендентные уравнения.
Алгебраическими уравнениями называются уравнения, в которых значение функции f(x) представляет собой полином n-й степени (n≥2). Всякое неалгебраическое уравнение называется трансцендентным. Функция f(x) в таких уравнениях содержит хотя бы одну из следующих функций: показательную, логарифмическую, тригонометрическую или обратную тригонометрическую.
Решением
уравнения f(x)=0
называется
совокупность корней![]() ,
при которых уравнение обращается в
тождество
,
при которых уравнение обращается в
тождество![]() .
Однако, точные значения корней могут
быть найдены аналитически только для
некоторых типов уравнений. Еще меньше
возможностей при получении точного
решения трансцендентных уравнений.
Следует отметить, что задача нахождения
точных значений корней не всегда
корректна. Так, если коэффициенты
уравнения являются приближенными
числами, точность вычисленных значений
корней заведомо не может превышать
точности исходных данных. Эти обстоятельства
заставляют рассматривать возможность
отыскания корней уравнения с ограниченной
точностью (приближенных корней).
.
Однако, точные значения корней могут
быть найдены аналитически только для
некоторых типов уравнений. Еще меньше
возможностей при получении точного
решения трансцендентных уравнений.
Следует отметить, что задача нахождения
точных значений корней не всегда
корректна. Так, если коэффициенты
уравнения являются приближенными
числами, точность вычисленных значений
корней заведомо не может превышать
точности исходных данных. Эти обстоятельства
заставляют рассматривать возможность
отыскания корней уравнения с ограниченной
точностью (приближенных корней).
З![]() адача
нахождения корня уравнения с заданной
точностью
(
адача
нахождения корня уравнения с заданной
точностью
(![]() >0)
считается решенной, если найдено
приближенное значение
>0)
считается решенной, если найдено
приближенное значение![]() ,
которое отличается от точного значения
корня
,
которое отличается от точного значения
корня
![]() не более чем на значение :
не более чем на значение :
Для отделения корней нелинейных уравнений применяются графический и аналитический методы. Для уточнения корней с заданной степенью точности существует множество численных методов. Самыми распространенными из них являются: метод Ньютона, метод хорд, метод итераций и метод половинного деления [3].
Процесс нахождения приближенного корня нелинейного уравнения состоит из двух этапов:
-
отделение корня уравнения (локализация корня на отрезке);
-
уточнение корня с заданной точностью.
Пример
2.1.1-1.
Отделить и уточнить корень уравнения 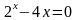 .
.
Согласно
теореме о существовании и единственности
корня на отрезке, найдем отрезок, на
концах которого функция
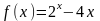 имеет
разные знаки, а первая производная
непрерывна и знакопостоянна (рис.
2.1.1-1).
имеет
разные знаки, а первая производная
непрерывна и знакопостоянна (рис.
2.1.1-1).
|
|
Рис. 2.1.1-1. Отделение корня нелинейного уравнения
Условия существования и единственности корня на отрезке [0;1] выполняются. Команды построения графика функции f(x) на отрезке [0;1] и график функции приведены на рис. 2.1.1-2.
|
|
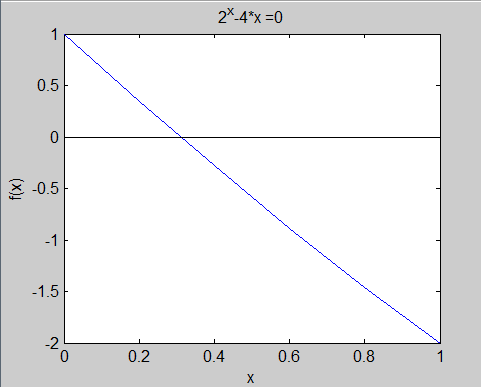
Рис. 2.1.1-2. Построение графика функции f(x)
Для решения нелинейных уравнений в среде Matlab используются встроенные функции: solve(), fzero(), root().
Функция fzero() используется для нахождения вещественных корней уравнений вида f(х)=0. Алгоритм, реализованный этой функцией, представляет собой комбинацию метода дихотомии (деления пополам), метода секущих и метода обратной квадратичной интерполяции. В простейшем варианте обращения кроме указателя на функцию, корень которой необходимо найти, задается окрестность х0, с которой начинается поиск: х = fzero(f, x0).
Аргумент f может быть задан одним из следующих способов:
-
формулой с неизвестным х, заключенной в апострофы;
-
именем m-файла (в апострофах и без расширения m);
-
указателем на функцию (например, @f_name).
Следует отметить, что выражение, заключенное в апострофы (левая часть уравнения) в качестве независимой переменной может иметь переменную только с именем х. Использование независимой переменной с другим именем вызовет сообщение об ошибке.
Аргумент х0 может быть задан одним из двух способов:
-
вектором [a;b], на концах которого функция f(x) меняет знак, что гарантирует нахождение, по крайней мере, одного корня на этом интервале;
-
скалярным значением, в окрестности которого предполагается нахождение корня (в этом случае функция fzero() сама пытается найти отрезок с центром в заданной точке х0, на концах которого функция f(x) меняет знак).
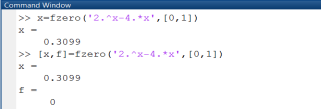
Из графика (рис. 2.1.1-2) следует, что корень находится на интервале [0;1]. Используем полученную информацию и обратимся к функции Matlab fzero(). При этом если мы хотим получить не только значение корня, но и узнать значение функции в найденной точке, то к функции Matlab fzero() можно обратиться с двумя выходными параметрами. На рис. 2.1.1-3 рассмотрено обращение к функции fzero() как с одним, так и с двумя выходными параметрами.
|
|
Рис. 2.1.1-3. Уточнение корня уравнения с использованием функции fzero()
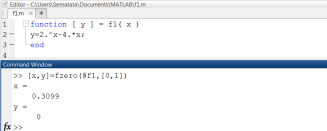
Вместо явного задания выражения для функции f(x) можно создать соответствующую функцию, запомнив ее в виде m-файла (рис. 2.1.1-4).
|
|
Рис. 2.1.1-4. Описание левой части в виде m-файла
Для символьного (аналитического) решения уравнений в MatLab используется функция solve(), которая может иметь следующие форматы:solve('f(x)',x),solve('f(x)'), где 'f(x)'– левая часть решаемого уравнения, заключенная в апострофах; x – искомая символьная неизвестная (описанная как syms x).
Рассмотрим технологию определения корня с помощью функции solve() на следующем примере (рис. 2.1.1-5).
Пример 2.1.1-2. Решить уравнение 2x–4∙x+3=0 аналитически.
|
|
Рис. 2.1.1-5. Уточнение корня уравнения с использованием функции solve()
Функция solve() в ряде случаев позволяет определить все корни уравнения f(x)=0. Она не требует информации о начальном значении корня или области его изоляции. Поэтому в случае решения ряда нелинейных уравнений, она не находит всех корней уравнения.
Функция
Matlab
roots()
используется для вычисления корней
полинома вида
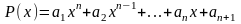 .
Перед ее использованием создается
список коэффициентов (даже нулевых), а
затем вводится сама функция roots(),
у которой в качестве аргумента указывается
имя списка коэффициентов (рис. 2.1.1-6).
.
Перед ее использованием создается
список коэффициентов (даже нулевых), а
затем вводится сама функция roots(),
у которой в качестве аргумента указывается
имя списка коэффициентов (рис. 2.1.1-6).
|
|
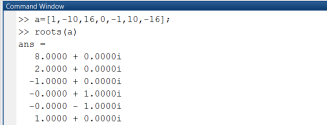
Рис. 2.1.1-6. Уточнение корня уравнения с использованием функции roots()
Вычисление
корней полинома
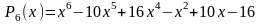 с использованием команды roots(а)
показало,
что у полинома есть четыре действительных
корня: х1=-1,
x2=1,
x3=2,
x4=8
и два мнимых корня x5=i
и x6=-i.
с использованием команды roots(а)
показало,
что у полинома есть четыре действительных
корня: х1=-1,
x2=1,
x3=2,
x4=8
и два мнимых корня x5=i
и x6=-i.




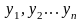
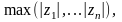 где
где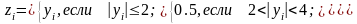
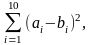 где
где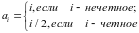
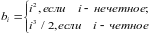
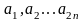 ,
состоящий из четного количества
элементов. Каждая пара чисел
,
состоящий из четного количества
элементов. Каждая пара чисел
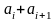 ,
где
,
где 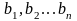 .
.
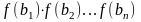 ,
где
,
где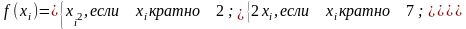
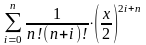
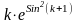 ,
где
,
где 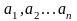 ,
где
,
где
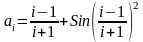 (
(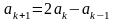 ,
где
,
где 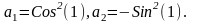
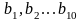 .
Преобразовать его таким образом, чтобы
сначала располагались нули, затем все
остальные элементы. Определить сумму
и количество элементов, значения
которых кратно 5
.
Преобразовать его таким образом, чтобы
сначала располагались нули, затем все
остальные элементы. Определить сумму
и количество элементов, значения
которых кратно 5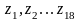 .
Создать из него массив
.
Создать из него массив 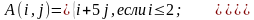
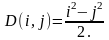 .
.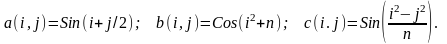
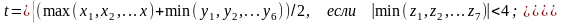
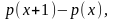 где
где
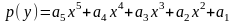
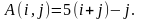 Удалить
из него столбцы, содержащие элементы,
меньшие 10
Удалить
из него столбцы, содержащие элементы,
меньшие 10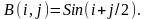 Определить наименьший элемент в каждой
строке матрицы и записать его в
соответствующий элемент вектора С.
Вывести полученный вектор С
Определить наименьший элемент в каждой
строке матрицы и записать его в
соответствующий элемент вектора С.
Вывести полученный вектор С