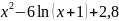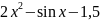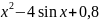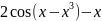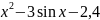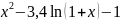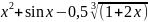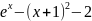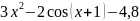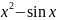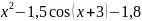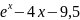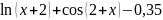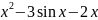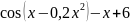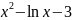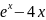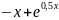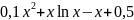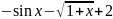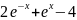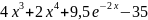Файл: Matlab Пособие.docx

2.4.2. Лабораторная работа по теме

«Технология решения обыкновенных

дифференциальных уравнений средствами MatLab»

1. Вопросы, подлежащие изучению

1. Нахождение символьного выражения производной от функции с использованием функции diff().

2. Вычисление числовых значений производных в точках.

3. Функции Matlab, предназначенные для решения ОДУ (ode23(), ode45()).

4. Вывод результатов решения ОДУ в виде таблицы.

5. Получение графического решения ОДУ.

2. Общее задание

1. Изучите материал Темы 2.4 (п. 2.4.1).

2. Выберите индивидуальный вариант задания из табл. 2.4.2-1.

3. Найдите символьное выражение производной от функции f(x) и вычислите значение производной от функции f(x) в произвольной точке с.

4. Найдите решение ОДУ на отрезке [a;b] с шагом h с использованием функций ode23() и ode45().

5. Создайте матрицу решений, записав в первый столбец аргумент, во второй и третий - решение, полученное с использованием функций ode23() и ode45(), а в четвертый столбец – погрешность метода (модуль разности решений ОДУ с использованием функций ode23() и ode45()).

6. Выведите полученную таблицу по столбцам.

7. Постройте графики полученных решений ОДУ в одном шаблоне.

8. Сохраните текст рабочего окна на внешнем носителе.

9. Представьте результаты работы преподавателю, ответьте на поставленные вопросы.

10. Выполните команду clear all.

11. Оформите отчет по выполненной работе.

2. Варианты индивидуальных заданий

Таблица 2.4.2-1

№	f(x)	ОДУ	Начальные условия	b	h
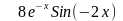
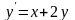
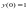
1				0,5	0,5
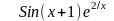
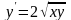
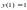
2				1.2
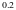
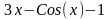
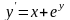
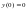
3				0.4
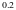
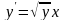
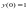
4				1	0,5
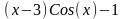
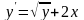
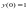
5				0.4	0,2
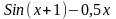
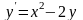
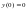
6				1
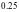
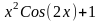
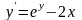
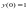
7				0.2	0,2
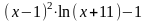
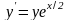
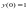
8				0.5	0,25
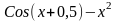
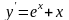
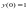
9				0,25
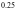
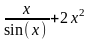
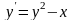
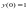
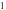
10					0,5
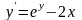
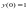
11				0,3	0,15
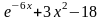
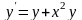
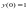
12				0,5	0,25
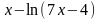
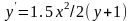
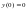
13				0,5	0.5
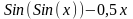
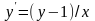
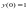
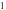
14					0,5
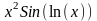
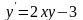
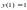
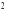
15					0,5
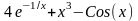
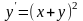
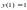
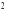
16					0,5
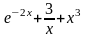
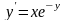
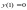
17				2	0,5
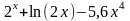
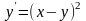
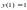
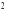
18					0,5
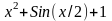
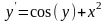
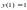
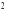
19					0,5
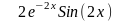
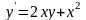
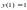
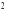
20					0,25
21
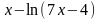
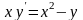
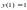
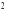
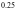
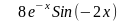
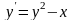
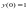
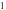
22					0,5
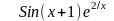
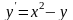
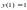
23				1,5	0,5
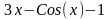
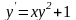
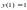
24				1.4
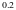
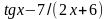
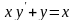
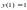
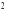
25					0,5
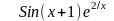
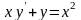
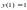
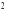
26					0,5
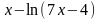
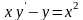
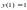
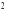
27					0,5
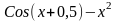
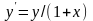
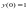
28				1,4	0,2
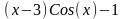
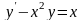
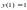
29				1,4	0,2
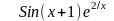
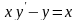
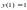
30				2	0.5

2. Содержание отчета

1. В форме комментариев:

• Название лабораторной работы

• ФИО студента, номер группы

• № варианта

• Индивидуальное задание

2. Протокол вычислений (сессии) в окне Command Window, снабженный необходимыми комментариями.

2.4.3. Контрольные вопросы по теме

1. Какие начальные условия должны быть заданы в соответствии с задачей Коши при решении ОДУ средствами системы Matlab?

2. Какие численные методы реализованы в функциях Matlab ode23() и ode45()?

3. Что является входными параметрами функций ode23() и ode45()?

4. В какой форме должны быть записаны функции ОДУ при использовании ode23() и ode45()?

5. Можно ли задать при решении ОДУ средствами Matlab требуемую точность вычислений?

6. Что представляет собой решение ОДУ второго порядка при использовании функций ode23() и ode45()?

7. Почему при решении ОДУ старших порядков необходимо использовать векторную функцию?

Тема 2.5. Технология решения задач одномерной оптимизации

2.5.1. Решение задач одномерной оптимизации функций

2.5.2. Лабораторная работа по теме «Технология решения задач

одномерной оптимизации»

2.5.3. Контрольные вопросы по теме

2.5.1. Решение задач одномерной оптимизации

При решении задачи поиска экстремума (максимума или минимума) функции y=f(x) одной переменной выделяют задачи поиска локального и глобального экстремума. При этом задача нахождения максимума целевой функции сводится к задаче нахождения минимума путем замены функции f(x) на -f(x), поэтому в дальнейшем будем говорить только о поиске минимума функции, то есть такого x*[a, b], при котором f(x*) = minf(x).

Интервал, на котором локализован единственный минимум, называется отрезком неопределенности.

Необходимым условием существования экстремума дифференцируемой функции f(x) является выполнение равенства f(х) = 0. Точка х, удовлетворяющая данному условию, называется точкой стационарности. Достаточным условием существования минимума в точке стационарности является выполнение неравенства f(х)>0, а максимума - f(х)<0.

Задача одномерной оптимизации имеет единственное решение в том случае, если функция f(x) на отрезке [a;b] имеет только один экстремум. Тогда говорят, что функция унимодальна на отрезке [a;b].

Достаточными условиями унимодальной функции на отрезке [a;b] являются:

- для дифференцируемой функции f(x) ее производная f(х) - неубывающая;

- для дважды дифференцируемой функции f(x) выполняется неравенство f(х)0.

Для решения задачи одномерной оптимизации с заданной степенью точности используются методы: дихотомии, золотого сечения, средней точки и многие другие [1]. При этом суть методов одномерного поиска заключается в том, что на каждой итерации интервал неопределенности уменьшается и стягивается к точке минимума. Уменьшение отрезка происходит до тех пор, пока на некоторой n-й итерации отрезок неопределенности b_n;a_n не станет соизмеримым с заданной погрешностью , то есть будет выполняться условие |b_n-a_n| <. Тогда за точку минимума можно принять любую точку, принадлежащую этому отрезку, в частности, его середину.

В MatLab поиск локального минимума осуществляет функция fminbnd(), имеющая следующий формат:

[x, y] = fminbnd(name, a, b), где:

name – имя функции, вычисляющей значение f(x);

a, b – границы интервала, на котором осуществляется поиск минимума;

x, y – координаты точки минимума на заданном интервале.

Чтобы с использованием функции Matlab fminbnd() вычислить локальный максимум, необходимо взять целевую функцию с противоположным знаком.

Пример 2.5.1-1. Найти локальный минимум функции .

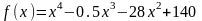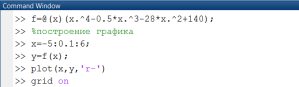
Решение задачи начнем с построения графика (рис. 2.5.1-1 и 2.5.1-2). Определим отрезок, содержащий точку минимума, исходя из вида графика функции. Если это возможно, то на этом отрезке следует провести полное исследование функции на унимодальность: от функции 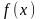получить и первую, и вторую производные и показать, что 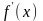должна быть неубывающей, а .

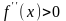Рис. 2.5.1-1. Построение графика функции f(x)

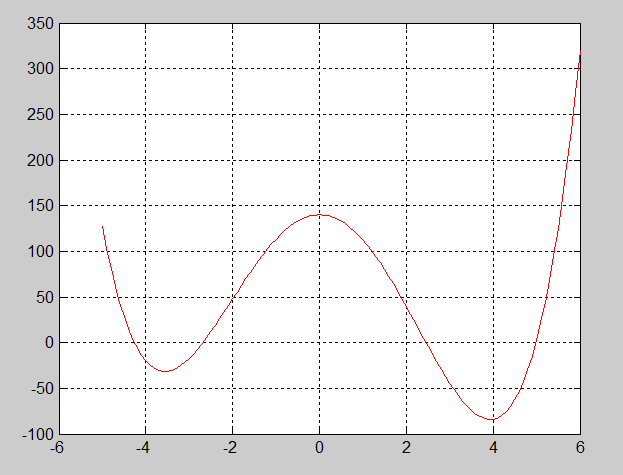
Рис. 2.5.9-2. График функции f(x)

Из графика следует, что на отрезках [-4;-3] и [3;5] имеются локальные минимумы. Исследуем функцию и поведение производных, например, на отрезке [3;5].

Для вычисления производных используем функцию Matlab diff(), имеющую следующий формат: diff(f, x, n). В качестве параметров этой функции используется:

• F – дифференцируемая функция;

• x – аргумент функции (переменная дифференцирования);

• n – порядок производной.

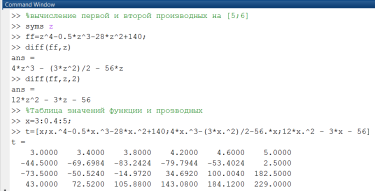
Получение значений функции и производных на выбранном отрезке приведено на рис. 2.5.1-3.

Рис. 2.5.1-3. Исследование функции f(x) на отрезке [3;5]

Из полученной таблицы значений функции и производных видно, что на отрезке [3;5] существует единственный минимум. Найдем координаты этого минимума с использованием функции Matlab fminbnd() (рис. 2.5.1-4).

Рис. 2.5.1-4. Нахождение координат точки минимума функции f(x)

2.5.2. Лабораторная работа по теме

«Технология решения задач одномерной оптимизации»

1. Вопросы, подлежащие изучению

1. Условие унимодальности функции на отрезке.

2. Получение таблиц значений функции и ее производных с использованием средств пакета Matlab.

3. Технология использования встроенной функции пакета Matlab – fminbnd().

2. Общее задание

1. Изучите материал Темы 2.5 (п. 2.5.1).

2. Выберите индивидуальное задание из табл. 2.5.2-1.

3. Постройте график функции f(x), выберите отрезок, содержащий минимум.

4. Проверьте на выбранном отрезке условие унимодальности функции, получив таблицу значений первой или второй производной.

5. Найдите координаты точки минимума f(x) с использованием встроенной функции Matlab fminbnd().

6. Сохраните текст рабочего окна на внешнем носителе.

7. Представьте результаты работы преподавателю, ответьте на поставленные вопросы.

8. Выполните команду clear all.

9. Оформите отчет по выполненной работе.

3. Варианты индивидуальных заданий

Таблица 2.5.2-1

1. Содержание отчета

1. В форме комментариев:

• Название лабораторной работы

• ФИО студента, номер группы

• № варианта

• Индивидуальное задание

2. Протокол вычислений (сессии) в окне Command Window.

2.5.3. Контрольные вопросы по теме

1. Понятия локального и глобального минимума функции.

2. Можно ли средствами Matlab вычислить глобальный минимум заданной функции?

3. Какие функции необходимо использовать перед поиском локального минимума?

4. Какая функция Matlab позволяет получить символьные выражения для производных от функции?

5. Назначение функции diff(f, x, n) и ее параметров.

6. Функция fminbnd(name, a, b) и назначение ее параметров.

7. Можно ли с использованием функции вычислить локальный максимум?