ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6255
Скачиваний: 13
31
4) находим минимальную ДНФ инверсии функции с учетом
неопределенных состояний;
5) найденную минимальную ДНФ инвертируем по теореме
де Моргана. В результате получим минимальную КНФ.
Рассмотрим несколько примеров.
Пример 1. Найти минимальную КНФ булевой функции, за-
данной в СДНФ:
f = (4, 5, 7, 10, 15).
[3, 8, 13, 14].
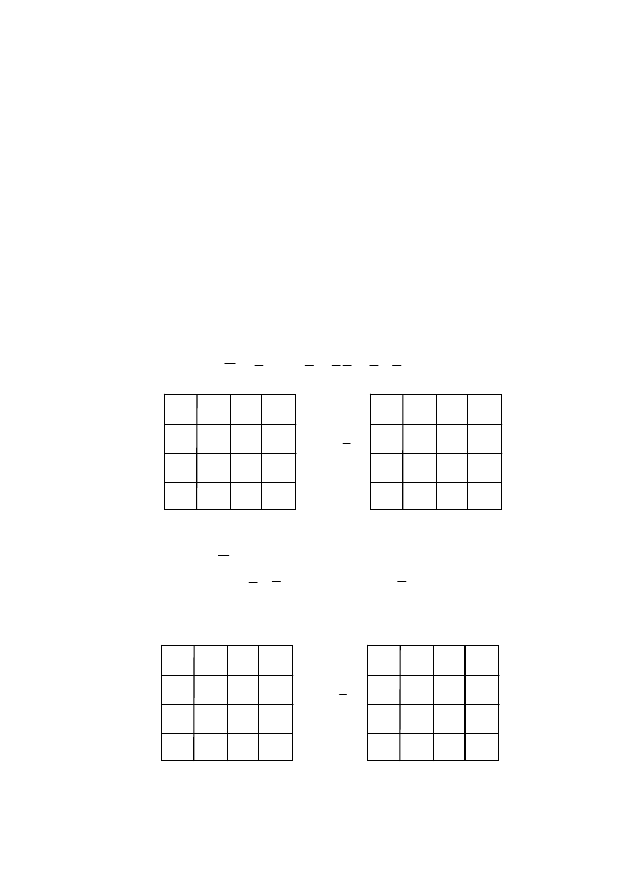
Решение. В соответствии с перечисленными пунктами на-
носим эту функцию на карту Вейча и на ней же отмечаем неоп-
ределенные состояния (рис. 33). На рис. 34 представлена инвер-
сия заданной функции.
Минимальная ДНФ инверсии заданной функции, найденная
с учетом неопределенных состояний, имеет вид (рис. 34):
.
f
BD
AC
AB
ACD
=
+
+
+
Рис. 33
1
1
1
1
1
Рис. 34
1
1
1
1
1
1
1
×
×
×
×
f =
f =
×
×
×
×
Инвертируем f и получаем искомую минимальную КНФ:
(
)(
)(
)(
).
f
B
D A
C A
B A C
D
=
+
+
+
+ +
Пример 2. Найти минимальную КНФ (рис. 35 и 36):
Рис. 35
1
1
1
1
1
Рис. 36
1
1
×
×
×
×
f =
f =
×
×
×
1
×
×
1
1
×
×
×
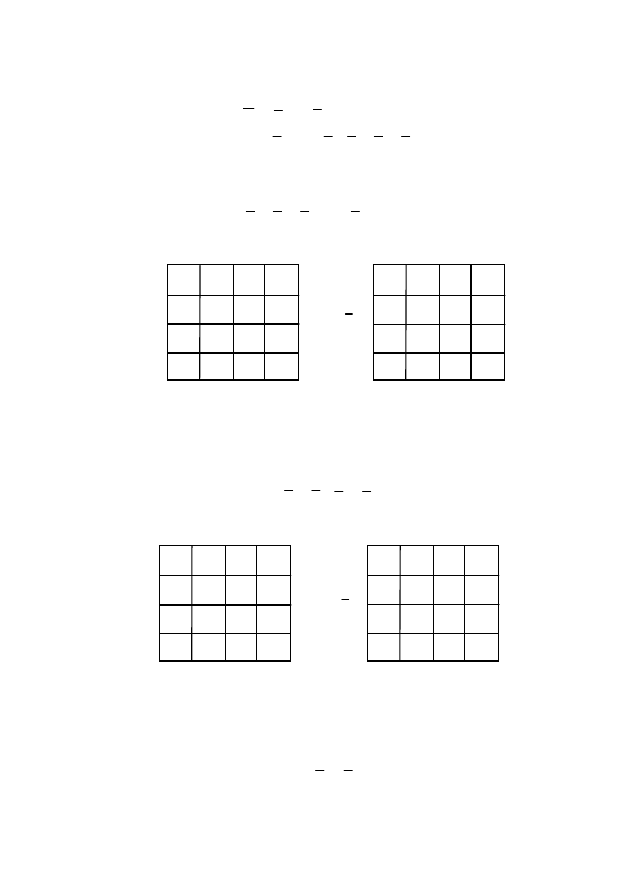
32
f = (0, 4, 6, 7, 10, 12).
[1, 2, 3, 8, 13, 15].
.
f
BD
CD
ABC
=
+
+
(
)(
)(
).
f
B
D C
D A
B
C
=
+
+
+ +
Пример 3. Найти минимальную КНФ (рис. 37 и 38):
f = (6, 7, 10, 11, 12).
[1, 2, 3, 4, 13].
(
)(
)(
).
f
A
B
C C
D B
C
=
+ +
+
+
Рис. 37
1
1
1
1
Рис. 38
1
×
×
×
f =
f =
×
×
×
×
1
1
×
×
1
×
1
1
1
Пример 4. Найти минимальную КНФ (рис. 39 и 40):
f = (0, 4, 6, 9, 12).
[1, 2, 3, 8, 13, 14].
(
)(
).
f
A
C B
D
=
+
+
Рис. 39
1
f =
×
×
1
×
×
×
1
Рис. 40
1
1
1
1
×
×
×
f =
×
×
1
×
1
1
×
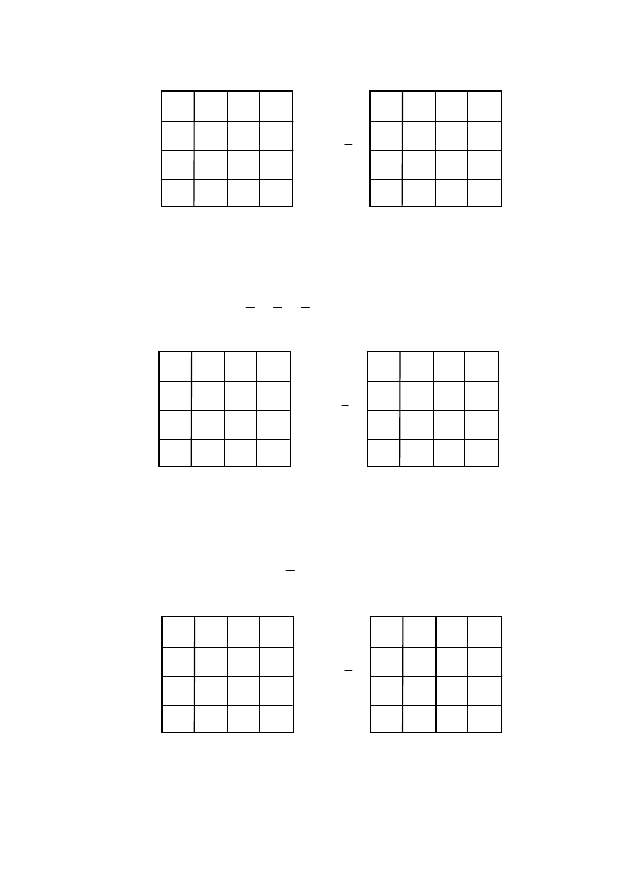
Пример 5. Найти минимальную КНФ (рис. 41 и 42):
f = (9, 10, 12, 14).
[1, 2, 3, 4, 8, 13].
(
).
f
A C
D
=
+
33
Рис. 41
1
f =
×
×
1
×
×
1
Рис. 42
1
1
1
1
×
×
×
f =
×
×
1
×
1
×
1
×
Пример 6. Найти минимальную КНФ (рис. 43 и 44):
f = (3, 7, 9, 10, 14).
[1, 2, 4, 8, 12, 13].
(
)(
)(
).
f
A
C
D A
D A C
=
+ +
+
+
Рис. 43
1
f =
×
×
×
1
Рис. 44
1
1
1
×
×
×
f =
×
×
1
×
1
×
1
×
1
×
1
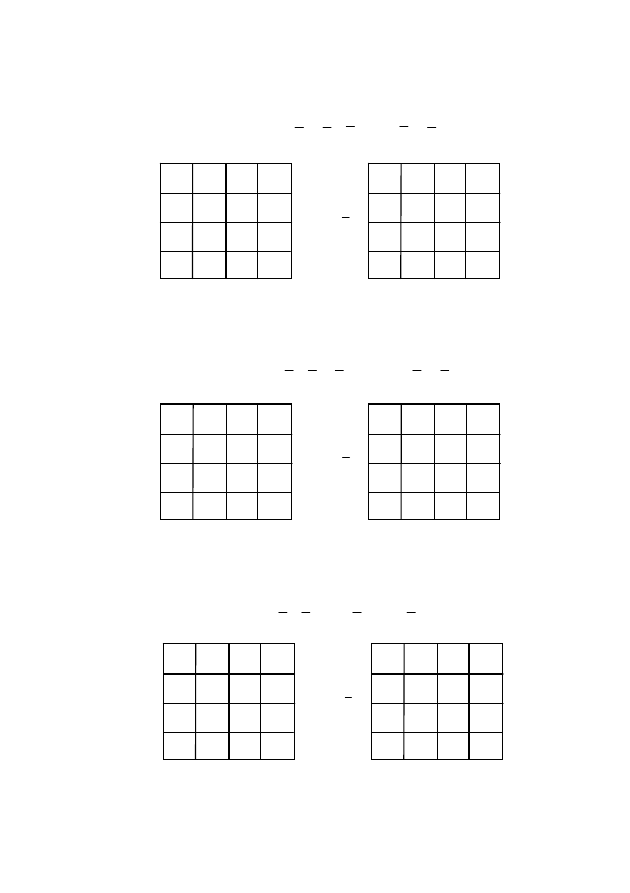
Пример 7. Найти минимальную КНФ (рис. 45 и 46):
f = (6, 7, 9, 10, 11, 15).
[1, 2, 4, 8, 13, 14].
(
)(
).
f
B
C A
B
=
+
+
Рис. 45
1
f =
×
×
×
1
Рис. 46
1
1
1
×
×
×
f =
×
×
1
×
×
×
1
×
1
1
1
34
Пример 8. Найти минимальную КНФ (рис. 47 и 48):
f = (3, 6, 9, 10, 12, 15).
[1, 2, 4, 8, 13, 14].
(
)(
)(
).
f
A C A
B
D A
B
C
D
=
+
+ +
+ + +
Рис. 47
1
f =
×
×
×
1
Рис. 48
1
1
1
×
×
×
f =
×
×
1
×
×
×
×
1
1
1
1
Пример 9. Найти минимальную КНФ (рис. 49 и 50):
f = (6, 9, 10, 15). [1, 2, 4, 12, 13].
(
)(
)(
)(
).
f
C
D A
D A
B
D B
C
D
=
+
+
+ +
+ +
Рис. 49
1
f =
×
×
×
1
Рис. 50
1
1
1
×
×
f =
×
×
1
×
×
×
1
1
1
1
1
Пример 10. Найти минимальную КНФ (рис. 51 и 52):
f = (3, 10, 15). [1, 2, 4, 9, 12, 13].
(
)(
)(
).
f
C A
B B
D A
B
D
=
+
+
+ +
Рис. 51
f =
×
×
×
1
Рис. 52
1
1
1
×
×
f =
×
×
1
×
×
×
1
1
1
1
1
×
×

35
3.4 Тема 5: «Операция импликации»
В задаче из контрольной работы на тему «Операция импли-
кации» необходимо представить в СДНФ, минимальной ДНФ и
минимальной КНФ заданное логическое выражение, содержа-
щее операцию импликации, возможно в различных сочетаниях с
дизъюнкцией, конъюнкцией и инверсией. Импликативные пре-
образования осуществляются с применением соотношения
.
P
Q
P
Q
→ = +
Пример 1. Представить в СДНФ, в минимальной ДНФ и
минимальной КНФ:
f = [(
)
(
)](
).
A
BD
C
D
A
BC
→
→
→
→
Решение. Сначала преобразуем выражения во всех круглых
скобках:
[(
)
(
)](
)
A
BD
C
D
A
BC
→
→
→
→
=
= [(
)
(
)](
).
A
BD
C
D
A
BC
+
→
+
+
Устраняем знак импликации из выражения, расположенно-
го в квадратных скобках:
f = [
](
).
A
BD
C
D A
BC
+
+ +
+
Применяем теорему де Моргана:
f = [ (
)
](
).
A B
D
C
D A
BC
+
+ +
+
Раскрываем скобки и находим СДНФ и минимальные ДНФ
и КНФ:
f = (
)(
)
AB
AD
C
D A
BC
+
+ +
+
=
AB
AD
AC
AD
ABC
ABCD
BC
BCD
=
+
+
+
+
+
+
+
=
= (0, 1, 2, 3, 4, 5, 6, 7, 10, 11) =
=
(
)(
).
A
BC
A
B A
C
+
=
+
+
Ответ.
СДНФ: f = (0, 1, 2, 3, 4, 5, 6, 7, 10, 11).
Минимальная ДНФ: f =
.
A
BC
+
Минимальная КНФ: f = (
)(
).
A
B A
C
+
+