ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6261
Скачиваний: 13

36
Пример 2. Представить в СДНФ, в минимальной ДНФ и
минимальной КНФ:
f = [
(
)]
.
A
BС
AB
D
A
BC
→
→
→
→ →
Решение. По аналогии с предыдущим примером сначала
преобразуем выражения в круглых скобках, а также под знаками
инверсии:
f = [(
)
(
)]
A
BС
A
B
D
A
BC
+
+
+ +
→ +
=
= [
]
.
A
BС
A
B
D
A
BC
+
+ + +
→ +
Выражение в квадратных скобках тождественно равно еди-
нице, так как в нем суммируются A и ,
A
следовательно:
f = 1
0
A
BC
A
BC
→ +
= + +
= (
)
A B
C
AB
AC
+
=
+
=
= (8, 9, 12, 13, 14, 15).
Ответ.
СДНФ: f = (8, 9, 12, 13, 14, 15).
Минимальная ДНФ: f =
.
AB
AC
+
Минимальная КНФ: f = (
).
A B
C
+
Заметим, что в минимальных ДНФ и КНФ переменная D
отсутствует. Это значит, что от аргумента D функция не зависит
(точнее, зависит несущественно). Но в заданной функции при-
сутствуют все четыре аргумента, поэтому СДНФ найдена в
предположении, что функция зависит не от трех аргументов, а
от четырех.
Пример 3. Представить в СДНФ, в минимальной ДНФ и
минимальной КНФ:
f = [(
)
(
)]
(
).
A
B
ABC
A ABC
C
AD
→
→
→
→
→
Решение. Преобразуем выражения в круглых скобках:
f = [(
)
(
)]
(
).
A
B
ABC
A ABC
C
AD
+
→
+
→
+
Устраняем знак импликации в квадратных скобках:
f = [
(
)]
(
)
A
B
ABC
A ABC
C
AD
+ +
+
→
+
=
= [
]
(
).
AB
ABC
A ABC
C
AD
+
+
→
+

37
Раскроем квадратные скобки. Получим нуль. Это значит,
что выражение, расположенное слева от стрелки, тождественно
равно нулю. Следовательно:
f = 0
(
)
C
AD
→
+
= 0
(
)
C
AD
+
+
= 1 (
)
C
AD
+
+
= 1.
Ответ:
СДНФ: f = (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15).
Минимальная ДНФ: f = 1.
Минимальная КНФ: f = 1.
3.5 Тема 6: «Дифференцирование булевых функций»
Решать задачи этого типа можно табличным способом. Од-
нако гораздо проще пользоваться формулой вида
( , , , )
( , , , 0)
( , , , 1),
f A B C D
f A B C
f A B C
D
∂
=
⊕
∂
(2)
где ( , , , 0)
f A B C
— нулевая остаточная функция,
( , , , 1)
f A B C
—
единичная остаточная функция. Проиллюстрируем нахождение
производных несколькими примерами.
Пример 1. Найти производную по
переменной D:
f = (0, 4, 6, 7, 8, 9, 11, 12, 13, 14, 15).
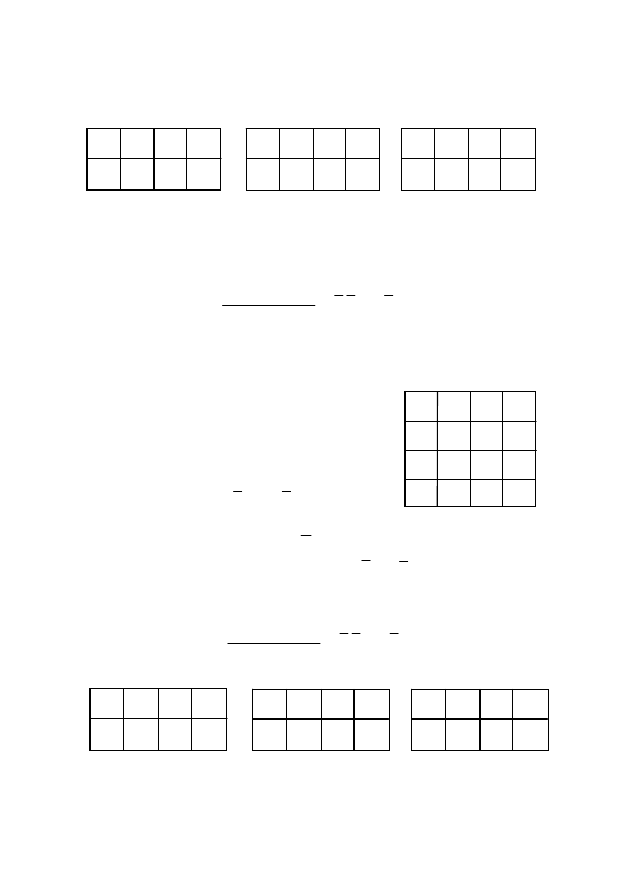
Решение. Нанесем функцию на кар-
ту Вейча (рис. 53) и найдем минималь-
ную ДНФ (в общем случае минимизация
не является обязательной. Функцию
можно оставить и в СДНФ. При этом ус-
ложнятся лишь алгебраические преобра-
зования):
.
f
C D
BC
AD
=
+
+
Находим остаточные функции по переменной D, так как по
этой переменной осуществляется дифференцирование заданной
функции:
( , , , 0)
f A B C
=
;
C
BC
+
( , , , 1)
f A B C
=
.
BC
A
+
Рис. 53
1
1
1
1
1
1
1
1
1
1
1
38
В соответствии с формулой (2) наносим их на карту Вейча
(рис. 54).
1
1
Рис. 54
1
1
1
1
1
1
1
1
1
1
⊕
=
1
1
На левой карте записана нулевая остаточная функция, на
средней — единичная, на правой — сумма по модулю 2, пред-
ставляющая собой результат дифференцирования:
( , , , )
.
f A B C D
AC
ABC
D
∂
=
+
∂
Это и есть ответ к заданному примеру.
Пример 2. Найти производную по переменной D:
f = (0, 1, 5, 6, 7, 8, 9, 10, 11, 13, 14,
15).
Решение. Как и в предыдущем слу-
чае, нанесем заданную функцию на кар-
ту Вейча (рис. 55) и найдем ее мини-
мальную ДНФ:
.
f
BC
CD
AB
=
+
+
Остаточные функции имеют вид:
( , , , 0)
f A B C
=
;
B
A
BC
+
( , , , 1)
f A B C
=
.
BC
C
AB
+ +
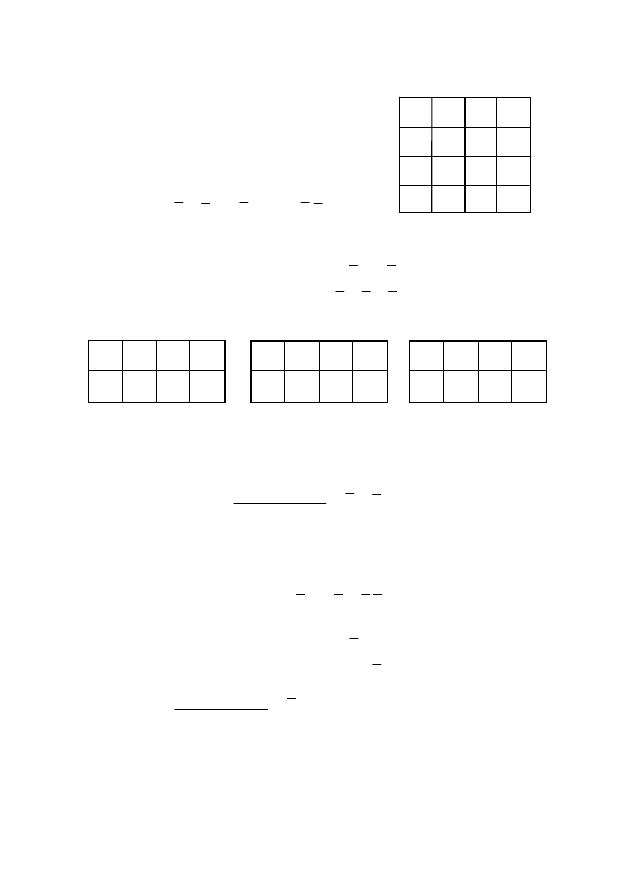
Наносим их на карты Вейча (рис. 56). Согласно этим картам
получаем искомую производную:
( , , , )
.
f A B C D
AC
BC
D
∂
=
+
∂
1
1
Рис. 56
1
1
1
1
1
1
1
1
⊕
=
1
1
1
1
Рис. 55
1
1
1
1
1
1
1
1
1
1
1
39
Пример 3. Найти производную по
переменной D:
f = (1, 3, 4, 7, 8, 9, 11, 12, 13).
Карта Вейча для этой функции при-
ведена на рис. 57. Находим минималь-
ную форму:
.
f
AC
BD
ACD
BC D
=
+
+
+
Наносим на карты Вейча остаточ-
ные функции, имеющие вид (рис. 58):
( , , , 0)
f A B C
=
;
AC
BC
+
( , , , 1)
f A B C
=
.
AC
B
AC
+ +
1
1
Рис. 58
1
1
1
1
1
1
1
⊕
=
1
1
1
1
1
Ответ: искомая производная имеет вид:
( , , , )
.
f A B C D
A
BC
D
∂
= +
∂
Пример 4. Найти производную по переменной D:
f = (0, 2, 4, 6, 12, 13, 14).
Решение. Находим минимальную ДНФ:
.
f
ABC
BD
AD
=
+
+
Остаточные функции имеют вид:
( , , , 0)
f A B C
=
;
A
B
+
( , , , 1)
f A B C
=
.
ABC
Ответ:
( , , , )
.
f A B C D
A
BC
D
∂
= +
∂
Пример 5. Найти производную по переменной D:
f = (1, 3, 7, 13, 15).
Рис. 57
1
1
1
1
1
1
1
1
1

40
Решение. Находим минимальную ДНФ:
.
f
ABD
BCD
ABD
=
+
+
Остаточные функции имеют вид:
( , , , 0)
f A B C
= 0;
( , , , 1)
f A B C
=
.
AB
BC
AB
+
+
Ответ:
( , , , )
f A B C D
D
∂
∂
=
.
AB
BC
AB
+
+
Пример 6. Найти производную по переменной D:
f = (0, 2, 6, 12, 14).
Решение. Находим минимальную ДНФ:
.
f
ABD
BCD
ABD
=
+
+
Остаточные функции имеют вид:
( , , , 0)
f A B C
=
;
AB
BC
AB
+
+
( , , , 1)
f A B C
= 0.
Ответ:
( , , , )
f A B C D
D
∂
∂
=
.
AB
BC
AB
+
+
Пример 6. Найти производную по переменной E, при усло-
вии, что функция зависит от пяти переменных и представлена в
аналитической форме следующим образом:
( , , , , )
.
f A B C D E
ABD
BCDE
ABDE
=
+
+
Решение. Находим остаточные функции:
( , , , ,0)
.
f A B C D
ABD
ABD
=
+
( , , , ,1)
.
f A B C D
ABD
BCD
=
+
Наносим их на карту Вейча (рис. 59), откуда получаем ми-
нимальную ДНФ искомой производной:
( , , , , )
f A B C D E
E
∂
∂
=
.
ACD
ABD
+