ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6262
Скачиваний: 13
41
1
1
1
1
1
1
1
Рис. 59
1
1
1
⊕
=
Найдем производную по переменной E табличным мето-
дом. Для этого найдем все остаточные функции при различных
наборах значений переменных A, B, C, D:
.
)
,
,
,
,
(
E
D
B
A
BCDE
ABD
E
D
C
B
A
f
+
+
=
.
0
0
1
1
0
0
0
0
0
0
)
,
0
,
0
,
0
,
0
(
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
E
E
E
f
.
1
1
1
1
0
0
1
0
0
)
,
1
,
0
,
0
,
0
(
E
E
E
E
f
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
.
0
0
1
1
0
1
0
0
0
0
)
,
0
,
1
,
0
,
0
(
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
E
E
E
f
.
1
1
1
1
1
0
1
0
0
)
,
1
,
1
,
0
,
0
(
E
E
E
E
f
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
.
0
0
0
1
0
0
1
0
1
0
)
,
0
,
0
,
1
,
0
(
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
E
E
E
f
.
0
1
0
1
1
0
1
1
1
0
)
,
1
,
0
,
1
,
0
(
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
E
E
E
f
.
0
0
0
1
0
1
1
0
1
0
)
,
0
,
1
,
1
,
0
(
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
E
E
E
f
.
1
0
1
1
1
1
1
1
0
)
,
1
,
1
,
1
,
0
(
E
E
E
E
f
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
.
0
0
1
0
0
0
0
0
0
1
)
,
0
,
0
,
0
,
1
(
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
E
E
E
f
.
0
1
1
0
1
0
0
1
0
1
)
,
1
,
0
,
0
,
1
(
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
E
E
E
f
.
0
0
1
0
0
1
0
0
0
1
)
,
0
,
1
,
0
,
1
(
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
E
E
E
f
.
0
1
1
0
1
1
0
1
0
1
)
,
1
,
1
,
0
,
1
(
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
E
E
E
f
.
0
0
0
0
0
0
1
0
1
1
)
,
0
,
0
,
1
,
1
(
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
E
E
E
f
.
1
1
0
0
1
0
1
1
1
1
)
,
1
,
0
,
1
,
1
(
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
E
E
E
f
.
0
0
0
0
0
1
1
0
1
1
)
,
0
,
1
,
1
,
1
(
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
E
E
E
f
.
1
1
1
0
0
1
1
1
1
1
1
)
,
1
,
1
,
1
,
1
(
=
+
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
E
E
E
E
f
Согласно этому списку на наборах 1, 3 и 7 функция меняет
свои значения с изменением переменной E, что полностью соот-
ветствует производной, представленной на рис. 59.
42
óÄëíú 3
íÖéêàü äéçÖóçõï ÄÇíéåÄíéÇ
1 íÂÒÚÓ‚Ó Á‡‰‡ÌËÂ
1.1 Асинхронный автомат на T-триггерах
Триггер типа T является одним из наиболее распространен-
ных на практике. Этот триггер имеет два установочных входа R
(нулевой) и S (единичный) и один управляющий вход, называе-
мый счетным. T-триггер меняет свое состояние с каждым им-
пульсом, поступившим на его счетный вход. При этом смена
состояний происходит под действием отрицательного фронта
импульса, т.е. когда напряжение переходит с высокого уровня
на низкий. На положительный фронт триггер не реагирует.
В простейшем случае триггер типа T применяют для по-
строения асинхронных автоматов, реализующих некоторую по-
следовательность состояний. Проиллюстрируем это на примере
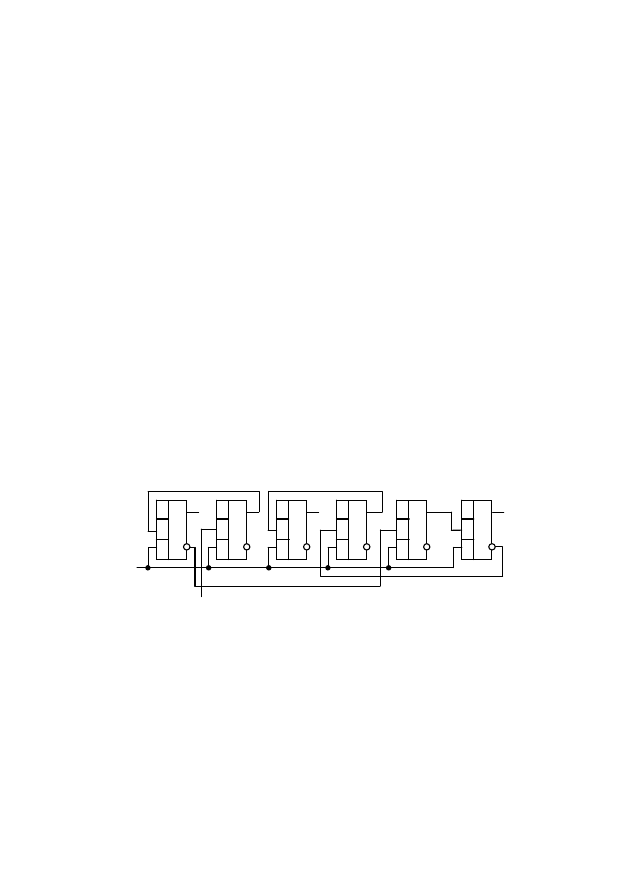
автомата, изображенного на рис. 1.
R
ТТ B
R
ТТ C
R
ТТ D
R
ТТ E
R
ТТ F
Y
2
5
2
4
2
3
2
2
2
1
2
0
Рис. 1
R
ТТ A
φ
Автомат состоит из шести T-триггеров A, B, C, D, E, F, об-
разующих двоичный регистр. Каждому триггеру поставлен в
соответствие определенный разряд двоичного числа. Веса на
рис. 1 указаны над триггерами в виде степеней числа 2.
Установим автомат в исходное состояние кратковременной
подачей низкого уровня напряжения на вход Y (т.е. на устано-
вочные нулевые R-входы). В регистре окажется число 000000.
Это значит, что на неинверсном выходе каждого триггера будет
низкий уровень напряжения, а на инверсном — высокий.

43
Подадим на вход φ прямоугольный импульс напряжения.
По его отрицательному фронту триггер B перейдет в единичное
состояние, и с его прямого выхода на счетный вход триггера A
поступит положительный фронт в виде перехода напряжения с
низкого уровня на высокий, на который триггер A не отреагиру-
ет, т.е. останется в нулевом состоянии. А так как триггер A свое
состояние не изменил, то и все остальные триггеры останутся в
прежних состояниях. Таким образом, после первого входного
импульса триггер B окажется в единичном состоянии, а все ос-
тальные — в нулевом и автомат окажется в состоянии 010000 (в
десятичной системе это 16).
Подадим на вход автомата второй импульс. По его отрица-
тельному фронту триггер B перейдет в нулевое состояние, в ре-
зультате чего триггер A получит отрицательный перепад напря-
жения (отрицательный фронт) и перейдет в единичное состоя-
ние. При этом на прямом выходе триггера A напряжение перей-
дет с низкого уровня на высокий, а на инверсном — наоборот: с
высокого на низкий. Следовательно, на счетный вход триггера E
поступит отрицательный фронт, вследствие чего триггер E пе-
рейдет в единичное состояние. На его прямом выходе сформи-
руется положительный фронт, т.е. напряжение перейдет с низ-
кого уровня на высокий. Этот положительный фронт поступит
на вход триггера F. Так как на положительный фронт триггер F
не реагирует, то он останется в нулевом состоянии и все осталь-
ные триггеры свои состояния не изменят. Таким образом, после
второго импульса автомат окажется в состоянии 100010 (в деся-
тичной системе 34).
Подадим на вход автомата третий импульс. В единичное
состояние перейдет только триггер B, а все остальные триггеры
останутся в прежних состояниях, поскольку на вход триггера A
поступит положительный фронт. Автомат окажется в состоянии
110010 (десятичное число 50).
Подадим на вход автомата четвертый импульс. Триггер B
перейдет в нулевое состояние и отрицательным перепадом на-
пряжения переведет в нулевое состояние триггер A. Все осталь-
ные триггеры останутся в прежних состояниях. Автомат устано-
вится в состояние 000010 (десятичное 2).

44
После пятого импульса состояние сменит только триггер B
и автомат окажется в состоянии 010010 (десятичное 18).
Подадим на вход φ шестой импульс. Триггер B перейдет в
нулевое состояние и отрицательным фронтом переведет триггер
A в единичное состояние. В результате на счетный вход тригге-
ра E поступит отрицательный перепад напряжения, и триггер E
перейдет в нулевое состояние. На прямом выходе триггера E
напряжение перейдет с высокого уровня на низкий. Под дейст-
вием этого перепада триггер F перейдет в единичное состояние.
На его инверсном выходе сформируется отрицательный фронт,
под действием которого триггер D перейдет в единичное со-
стояние. На прямом выходе триггера D сформируется положи-
тельный перепад напряжения. Этот перепад поступит на вход
триггера C. Так как фронт положительный, то триггер C оста-
нется в нулевом состоянии. Таким образом, после шестого им-
пульса автомат окажется в состоянии 100101 (десятичное 37).
После седьмого импульса автомат перейдет в состояние
110101 (десятичное 53), после восьмого — 000101 и т.д.
1.2 Тест на тему № 6 «Асинхронный автомат»
Цель данного теста выяснить, насколько тестируемый усво-
ил принцип работы T-триггера и построенных на его основе
асинхронных автоматов. Формулируется тестовое задание сле-
дующим образом: «Автомат находится в состоянии t. В каком
состоянии будет находиться автомат, если на его вход φ подать
два прямоугольных импульса?»
Ответ необходимо представить в десятичной системе.
Проиллюстрируем выполнение этого задания на примере
автомата, приведенного на рис. 1, для t = 27. Переведем число
27 в двоичную систему:
10
2
27 |
11011| .
=
Получилось пятизначное число, а триггеров в регистре 6.
Следовательно, к найденному двоичному числу слева добавляем
нуль: 011011. Будем считать, что это заданное исходное состоя-
ние автомата (рис. 1):

45
A = 0, B = 1, C = 1, D = 0, E = 1, F = 1.
Подадим на вход φ импульс. Автомат перейдет в состояние
101000. Подадим на вход φ второй импульс. Автомат перейдет в
состояние 111000. Переводим число 111000 в десятичную сис-
тему. Получим 56.
Это и есть ответ к данному тестовому заданию.
2 Задачи из письменной кÓÌÚðÓθÌой ð‡·ÓÚ˚
2.1 Тема 7: «Синтез преобразователя кодов»
О весовых и невесовых кодах. Пусть дано двоичное чис-
ло, например, 11010. Какое десятичное число ему соответству-
ет? В общем случае однозначно ответить на этот вопрос невоз-
можно из-за недостатка информации. Если это невесовой дво-
ичный код, то необходима таблица, где для каждого кода указа-
но соответствующее десятичное число. Соответствие может
быть задано не только таблицей, но и какими-либо формулами
или правилами (примером может служить код Грея, задаваемый
формулами [1, с. 341]).
В весовых системах таблицы не требуются. Перевод двоич-
ных кодов в десятичную систему осуществляется на основе по-
линома вида
1
1
2
2
1 1
0 0
,
n
n
n
n
N
a
q
a
q
a q
a q
−
−
−
−
=
+
+
+
+
…
где коэффициенты
1
0
,
,
n
a
a
−
…
изображают цифры; n — длина
кода, т.е. число входящих в него знаков 0 или 1. Числа
1
2
1
0
,
,
,
,
n
n
q
q
q
q
−
−
…
обозначают веса. Именно этими весами
и обусловлено все многообразие систем двоичного кодирования
чисел, представленных в других системах счисления.
Самым распространенным весовым двоичным кодом явля-
ется код, построенный на обычной двоичной системе счисления
с весами, равными степени числа 2: 1, 2, 4, 8, 16, 32, … Напри-
мер, если n = 5, то
4
3
2
1
0
16,
8,
4,
2,
1.
q
q
q
q
q
=
=
=
=
=
Тогда коду 11010 соответствует десятичное число
1
⋅16 + 1⋅8 + 0⋅4 + 1⋅2 + 0⋅1 = 26.