Файл: Теоретические основы развития внимания младших школьников при изучении арифметических действий.docx
Добавлен: 06.11.2023
Просмотров: 188
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Умножение и деление многозначных чисел.
Умножение и деление многозначных чисел представляет гораздо больше трудностей, чем сложение и вычитание. Это связано с тем, что ученики не твердо знают таблицу умножения. Даже те учащиеся, которые запоминают таблицу умножения, затруднялись применить её при решении примера с многозначными числами, то есть актуализировать свои знания и использовать их.
Трудности возникают и тогда, когда надо единицы высшего разряда перевести в низший разряд, удержать их в памяти. Неумение долгое время сосредоточить внимание на выполнение действия приводит к тому, что учащиеся низшие разряды числа умножают правильно, а при умножении высших разрядов допускают ошибки.
Вариативный подход к решению арифметических задач
В условиях стремительных изменений в обществе меняются и требования к современному ученику. Он должен обладать более широкими взглядами на жизнь, большим спектром вариантов выхода из предлагаемых ситуаций, быть более мобильным. И основная задача в формировании навыков вариативности ложится на плечи учителя начальных классов, так как именно он определяет основные принципы учебной деятельности. Креативный подход к учебному материалу, по нашему мнению, должен стать неотъемлемой частью всей учебной деятельности учащегося, красной линией проходит через весь процесс обучения и воспитания. И как нельзя лучше для начального обучения вариативности подходят уроки математики.
Так, при работе с текстовыми задачами могут быть использованы разные приемы. Учителя, как правило, не останавливаются на этом из-за нехватки времени на уроке, переходят к следующему заданию. Эту же проблему поднимает и Л.В.Болотник в своей книге «Дидактические возможности учебников по математике для начальной школы». Покажем эти приемы на примере решения одной составной задачи. Мы их подразделяем на две группы.
I. 1. Придумай задачу, обратную данной.
Такой прием заставит ученика не только еще раз вернуться к содержанию задачи и осмыслить логику решения и принципы построения задачи, но и построить собственную, обратную логическую цепь рассуждений и умозаключений, организуемых в условии новой задачи. Например:
С первого участка собрали 98 килограммов картофеля. Со второго – на 6 килограммов больше, чем с первого. Сколько килограммов картофеля собрали с третьего участка, если всего собрали 270 килограммов картофеля?
Задача, обратная данной, будет звучать так:
С первого участка собрали 98 килограммов картофеля, со второго – на 6 килограммов больше, чем с первого, а с третьего – на 30 килограммов меньше, чем с первого. Сколько килограммов картофеля собрали со всех трех участков?
2. Поиск различных способов решения.
Следует отметить, что этот прием подходит только для тех задач, которые имеют несколько способов решения. Здесь важно показать ученику логику решения каждым из способов, дать сравнительную характеристику решений, проанализировать ход решения каждого способа. Тогда решение вышеприведенной задачи будет выглядеть следующим образом.
I способ.
1) 98 + 6 = 104 (кг) – со II участка;
2) 270 – 98 = 172 (кг) – со II и III участков;
3) 172 – 104 = 68 (кг) – с III участка.
Запишем это решение выражением:
270 – 98 – (98 + 6) = 68 (кг) – с III участка.
II способ.
98 + 6 = 104 (кг) – со II участка;
98 + 104 = 202 (кг) – с I и II участков;
270 – 202 = 68 (кг) – с III участка.
Выражение этого решения будет выглядеть так:
270 – [98 + (98 + 6)] = 68 (кг) – с III участка.
3. Решение задачи через введение переменной.
Такой прием позволяет уже на ранних этапах обучения математике знакомить детей с уравнением, закрепляет их знания в области поиска «неизвестного». Например, чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность. Аналогично по ситуации проговариваются все действия с арифметическими компонентами действий. Такая работа позволяет закрепить алгоритм нахождения неизвестного, абстрагировать процесс его нахождения.
Обозначим через х количество картофеля, собранного с IIIучастка. Тогда будет такое уравнение: 270 = 98 + 104 + х.
4. Составление аналогичной задачи с новыми данными.
Этот прием помогает детям переносить уже известную схему решения на другие задачи этого вида, учит обобщать их в группы.
В магазине игрушек на полках стояло 560 игрушек трех видов. Слоников было 111 штук, а медвежат – на 45 штук больше. Сколько на полках было лисят?
5. Постановка дополнительных вопросов к решенной задаче.
Подобная работа предполагает постановку дополнительных вопросов, замену известных величин неизвестными и поиск новых решений, стимулирует мысль ученика, заставляет его анализировать и сравнивать несколько схем решения задач. Например:
«Как изменился бы ход решения задачи, если бы было не известно, сколько килограммов картофеля собрано со IIучастка, при известной массе картофеля, собранной с I и IIIучастков? На сколько больше килограммов картофеля собрали сI участка, чем с III? На сколько больше килограммов картофеля собрали с I и II участков вместе, чем с III?»
6. Записать решение задачи выражением.
Подобная работа помогает ребенку не только увидеть решение задачи в целом, но и закрепить порядок записи арифметических действий, навык грамотного использования скобок и двойных скобок. Применительно к нашей задаче выражение будет выглядеть так:
270 – 98 – (98 + 6) = 68 (кг) – с III участка.
Или: 270 – [98 + (98 + 6)] = 68 (кг) – с III участка.
II.1. Составление задачи по выражению.
Например, по выражению 6 – 3 можно составить задачи на нахождение меньшего, остатка, разницы.
На нахождение меньшего:
У Димы было 6 машинок, а у Пети – на 3 меньше. Сколько машинок было у Пети?
На нахождение разницы:
У Димы 6 машинок, а у Пети – 3. На сколько машинок у Димы больше, чем у Пети?
На нахождении остатка:
У Димы было 6 машинок. Он подарил Пете 3 машинки. Сколько машинок у него осталось?
Использование схем при решении составных задач (когда составную задачу расчленяют на простую) помогает даже слабоуспевающим ученикам разбираться в задачах, устанавливать взаимосвязь между величинами.
Например, возьмем задачу на пропорциональную зависимость.
В 4 одинаковых ящиках было 28 кг апельсинов. Сколько килограммов апельсинов в 8 таких ящиках?
Вначале составляем краткую запись задачи в виде схемы. Дети работают в тетрадях, используя разные цвета, а учитель – на доске с цветными мелками.
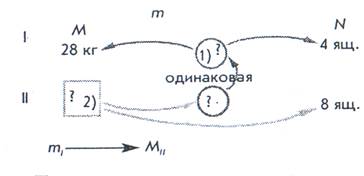
Перед учителем всегда должен стоять вопрос, как провести необходимое для поиска решения задачи рассуждение наиболее доступным младшему школьнику образом. Сначала нужно выявить зависимости между величинами.
Рассуждение начинаем с главного вопроса задачи. Возьмем красный цвет и выделим главный вопрос задачи квадратиком прямо на ее краткой записи. Ставиться вопрос: что нужно, чтобы найти массу 8 ящиков? (Используем схему). Красным цветом от главного вопроса задачи ведем 2 стрелки: к числу 8 (количество ящиков) и к знаку вопроса (масса 1 ящика). Вычленилась простая задача. Неизвестна масса 1 ящика. Знак вопроса обводим зеленым кружочком. Теперь ставится вопрос: что нужно сделать, чтобы найти массу 1 ящика? Зеленым цветом ведем стрелки к числам 4 (количество ящиков) и 28 кг (масса всех ящиков). Затем на краткой записи устанавливаем порядок действий (обратный ход), в кружочках отмечаем порядок действий. Таким образом, отчетливо видно, что составная задача имеет 2 действия решения. Использование разных цветов помогает устанавливать количество действий задачи и взаимосвязь между величинами.
В конце вычленяем простые задачи:
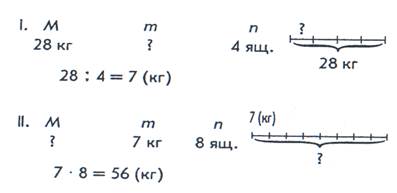
Представление составной текстовой задачи в виде последовательной цепочки простых задач способствует развитию логического мышления.
Обучение детей младшего школьного возраста аналитическому способу рассуждения при решении задач уместно начинать с задач в два действия, затем постепенно усложнять их.
Такая методика работы над задачей способствует развитию у детей умения мыслить. Действительно, математические рассуждения с присущими им четкостью, последовательностью и логичностью являют собой пример правильно организованного мышления, а владение математическим языком, понимание точного смысла утверждений и связей между логическими конструкциями в тексте задачи оказывают существенное влияние на языковое развитие личности и тем самым вносят весомый вклад в формирование и развитие мышления человека в целом.
Применение предлагаемых приемов работы над текстовой задачей формирует еще и такое немаловажное качество личности, как умение рассуждать.
Таким образом, научить простейшим операциям анализа, синтеза, сравнения на примере решения текстовых задач с целью перенесения усвоенных знаний, умений, навыков в другие сферы деятельности учащихся – и есть первостепенная задача учителя начальных классов. Для этого необходимо:
1) научить детей находить нужные умозаключения, чему, собственно, и учит математика;
2) научить располагать эти умозаключения в правильном порядке.
Таким образом, формирование вариативного подхода к решению текстовых задач имеет глубокие цели и задачи, ведет в конечном итоге к формированию конкурентоспособной личности выпускника школы.
Использование различных способов решения арифметических задач в развитии внимания младших школьников
В практике часто наблюдается, что вопрос о решении задачи различными способами возникает только тогда, когда в учебнике дано задание: решите задачу различными способами. Но так как такие задания обычно сопровождают задачи, решения которых связаны со свойствами арифметических действий, то у учащихся формируется определенное представление о возможности решения задачи различными способами и оно связывается только со свойствами арифметических действий. Думается, что работа, связанная с решением задач различными способами, не может и не должна ограничиваться только этим. Более того, работа над задачей должна специальным образом организовываться, чтобы учащимся было легко осознать возможность ее решения различными способами.
Безусловно, некоторые ученики способны и самостоятельно предложить различные способы решения задачи в силу своих индивидуальных особенностей мышления, но с большинством учащихся необходимо проводить в этом плане целенаправленную работу, используя для этой цели различные методические приемы.
В школьном курсе математики есть понятия, о которых еще рано говорить в начальной школе, но готовить учеников к их сознательному восприятию все же необходимо. Одним из таких понятий является функция. Возможность для формирования первых функциональных представлений появляется уже в процессе обучения учащихся решению текстовых задач.
К тому моменту, когда школьники изучат смысл основных арифметических действий и познакомятся с кратным сравнением чисел, в курсе математики появляются задачи на прямую и обратную пропорциональные зависимости величин, где возникает необходимость устанавливать взаимосвязи и находить зависимость между данными и искомым. Традиционно эти задачи решаются так называемым способом приведения к единице, суть которого заключается в нахождении сначала, например, цены, количества материала (на одно изделие) и т.д., а затем искомой в задаче величины.
Среди задач на пропорциональную зависимость величин встречаются задачи, в которых числовые данные находятся в некотором отношении, что предполагает еще один способ решения, представляющий интерес с точки зрения функциональной пропедевтики.