Файл: Реферат по дисциплине Математическое моделирование на тему транспортная задача.docx
Добавлен: 07.11.2023
Просмотров: 192
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Кузбасский государственный технический университет имени Т.Ф. Горбачева»
Институт профессионального образования
Кафедра теории и методики профессионального образования
РЕФЕРАТ
по дисциплине «Математическое моделирование» на тему:
ТРАНСПОРТНАЯ ЗАДАЧА
Выполнили ст. гр. ИСт-192
Зайцева Я. С.
Сагдатдинова А. В.
Преподаватель Кузнецов И. С.
Кемерово 2022
Оглавление
Введение 3
Глава 1. Математическая постановка задачи 4
1.1 Определение опорного плана. 7
Глава 2. Методы решения транспортной задачи. 8
2.1 Метод северо-западного угла 8
2.2 Метод минимального элемента 10
2.3 Метод аппроксимации Фогеля 13
2.4 Метод потенциалов 18
Заключение 28
Список использованной литературы и Интернет-ресурсов 29
Введение
Каждый человек ежедневно, не всегда осознавая это, решает проблему: как получить наибольший эффект, обладая ограниченными средствами. Чтобы достичь наибольшего эффекта, имея ограниченные средства, надо составить план, или программу действий - для этого существует целый раздел под названием математическое программирование.
Одним из классов математических моделей являются задачи линейного программирования. Одной из задач линейного программирования является транспортная задача - задача составления оптимального плана перевозок, позволяющего минимизировать суммарный километраж.
Транспортная задача делится на два вида: транспортная задача по критерию стоимости - определение плана перевозок, при котором стоимость груза была бы минимальна; транспортная задача по критерию времени - более важным является выигрыш по времени.
Транспортная задача по критерию стоимости является частным случаем задачи линейного программирования и может быть решена симплексным методом.
Однако в силу особенностей задачи, она решается намного проще.
Целью транспортной задачи является обеспечение доставки товара потребителю в нужное время и место при минимально возможных совокупных затратах трудовых, материальных, финансовых ресурсов.
Цель транспортной деятельности считается достигнутой при выполнении шести условий: нужный товар необходимого качества в необходимом количестве доставлен в нужное время в нужное место с минимальными затратами.
Объектом изучения являются материальные и соответствующие им финансовые, информационные потоки, сопровождающие производственно-коммерческую деятельность.
В данной работе будут рассмотрены понятие транспортной задачи, её типы, различные методы решения.
Глава 1. Математическая постановка задачи
Общая постановка транспортной задачи заключается в определении оптимального плана перевозок некоторого однородного груза из пунктов отправления
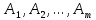 в пункты назначения
в пункты назначения 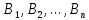 . Критерием оптимальности берётся минимальная стоимость перевозки или минимальное время доставки груза.
. Критерием оптимальности берётся минимальная стоимость перевозки или минимальное время доставки груза.Рассмотрим транспортную задачу, где в качестве критерия оптимальности взята минимальная стоимость перевозок всего груза. Обозначим через
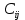 тарифы перевозки единицы груза из пункта отправления i в пункт назначения j. Обозначим через
тарифы перевозки единицы груза из пункта отправления i в пункт назначения j. Обозначим через 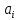 запасы груза в i-м пункте отправления, а через
запасы груза в i-м пункте отправления, а через 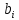 потребности груза в j-м пункте назначения, а через
потребности груза в j-м пункте назначения, а через 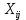 количество единиц груза перевозимого из пункта отправления i в пункт назначения j.
количество единиц груза перевозимого из пункта отправления i в пункт назначения j.Тогда математическая модель транспортной задачи состоит в определении минимального значения функции
F =
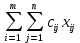 (форм. 1)
(форм. 1)при условиях
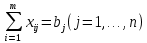 (форм. 2)
(форм. 2) 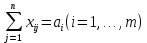 (форм. 3)
(форм. 3)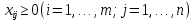 (форм. 4)
(форм. 4)Поскольку удовлетворяются условия (форм. 2) – (форм. 4), то обеспечивается доставка необходимого количества груза в каждый из пунктов назначения, вывоз груза из всех пунктов отправления, а также исключаются обратные перевозки.
Определение 1. Любое неотрицательное решение
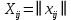 (i=1,..,m; j=1,...,n) систем (форм. 2) и (форм. 3) называется допустимым планом транспортной задачи.
(i=1,..,m; j=1,...,n) систем (форм. 2) и (форм. 3) называется допустимым планом транспортной задачи.Определение 2. План
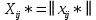 (i=1,..,m; j=1,...,n) при котором функция (форм. 1) принимает минимальное значение, называется оптимальным планом транспортной задачи.
(i=1,..,m; j=1,...,n) при котором функция (форм. 1) принимает минимальное значение, называется оптимальным планом транспортной задачи.Если сумма груза у поставщиков равна общей сумме потребностей в пунктах назначения:
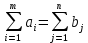 (форм. 5)
(форм. 5)то модель транспортной задачи называется закрытой (или сбалансированной). Если (форм. 5) не удовлетворяется, то модель транспортной задачи называется открытой (или несбалансированной).
Теорема 1. Для разрешимости транспортной задачи необходимо и достаточно, чтобы выполнялось условие (форм. 5).
В случае превышения запаса над потребностью, т.е. при
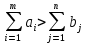 (форм. 6)
(форм. 6)вводится фиктивный (n+1)-ый пункт назначения с потребностью
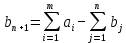 (форм. 7)
(форм. 7)Соответствующие тарифы считаются равными нулю:
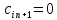 (i=1,...,m). После этих преобразований получим закрытую модель транспортной задачи.
(i=1,...,m). После этих преобразований получим закрытую модель транспортной задачи.Аналогично, при
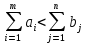 (форм. 8)
(форм. 8)вводится фиктивный (
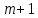 ) пункт отправления с грузом,
) пункт отправления с грузом, 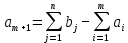
(форм. 9)
а тарифы полагаются равными нулю:
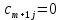 (j=1,...,n). После этих преобразований получим закрытую модель транспортной задачи.
(j=1,...,n). После этих преобразований получим закрытую модель транспортной задачи.Мы рассмотрим закрытую модель транспортной задачи. Если же модель транспортной задачи будет является открытой, то с помощью вышеизложенных преобразований строим закрытую модель транспортной задачи.
Обычно данные транспортной задачи записывают в виде таблицы:
| Пункты отправления | Пункты назначения | Запасы | |||||
| B1 | … | Bj | … | Bn | |||
| A1 | c11 x11 | … … | c1j x1j | … … | c1n x1n | a1 | |
| … | … … | … … | … … | … … | … … | … | |
| Ai | ci1 xi1 | … … | cij xij | … … | cin xin | ai | |
| … | … … | … … | … … | … … | … … | … | |
| Am | cm1 xm1 | … … | cmj xmj | … … | cmn xmn | am | |
| Потребности | b1 | … | bj | … | bn | | |
Число переменных
 равно
равно 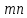 , где m число пунктов отправления, а n число пунктов назначения. Число уравнений в (форм. 2) и (форм. 3) равно
, где m число пунктов отправления, а n число пунктов назначения. Число уравнений в (форм. 2) и (форм. 3) равно
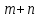 . Так как мы рассматриваем закрытую модель транспортной задачи (выполняется равенство (рис. 5)), то число линейно независимых уравнений равно
. Так как мы рассматриваем закрытую модель транспортной задачи (выполняется равенство (рис. 5)), то число линейно независимых уравнений равно 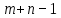 . Следовательно, опорный план транспортной задачи может иметь не более
. Следовательно, опорный план транспортной задачи может иметь не более 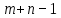 отличных от нуля неизвестных.
отличных от нуля неизвестных.Если в опорном плане количество отличных от нуля компонентов равно в точности
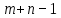 , то опорный план называется невырожденным, а если меньше − то вырожденным.
, то опорный план называется невырожденным, а если меньше − то вырожденным.Для решения транспортной задачи сначала определяется начальный опорный план, а затем определяется оптимальный план путём улучшения текущего опорного плана.
Для определения начального опорного плана существует несколько методов. Мы рассмотрим три метода. Метод северо-западного угла, метод минимального элемента, метод аппроксимации Фогеля и метод потенциалов.