Файл: Реферат по дисциплине Математическое моделирование на тему транспортная задача.docx

2.4 Метод потенциалов

Процедура нахождения оптимального плана транспортной задачи имеет два этапа. На первом этапе находят опорной план транспортной задачи. Далее последовательно улучшают найденный опорный план до получения оптимального плана.

Для определения опорного плана будем пользоваться методом северо-западного угла, методом минимального элемента или методом аппроксимации Фогеля, рассмотренных выше.

При применении этих методов получаем занятых клеток в исходном плане. Отметим, что в некоторых клетках могут стоять нули. Полученный план следует проверить на оптимальность.

Теорема. Если для некоторого опорного плана (i=1,..,m; j=1,...,n) транспортной задачи существуют такие числа 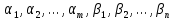, что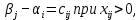



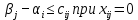(форм. 10)

для всех i=1,..,m; j=1,...,n, то − это оптимальный план транспортной задачи.

Определение3. Числа 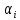 и 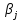 (i=1, .., m; j=1, ..., n) называются потенциалами пунктов отправления и пунктов назначения, соответственно.

Вышеизложенная теорема позволяет построить алгоритм нахождения оптимального плана транспортной задачи.

Алгоритм состоит в следующем. Предположим, что одним из рассмотренных выше методов найден опорный план транспортной задачи. Для каждого из пунктов отправления и назначения определяют потенциалы 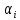  и 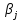  (i=1,..,m; j=1,...,n) из системы уравнений

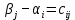(форм. 11)

где 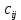− тарифы транспортной задачи в заполненных клетках.

Так как число заполненных клеток равно

---

, то система (форм. 11) с неизвестными содержит уравнений. Для решения данной задачи одно из неизвестных можно сделать равным нулю и найти остальные неизвестные. После этого, для свободных клеток определяем числа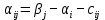

(форм. 12)

Если среди чисел 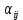нет положительных, то найденный опорный план является оптимальным. Если же для некоторой свободной клетки 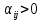, то данный опорный план не является оптимальным и необходимо перейти к новому опорному плану. Для этого рассматривают все свободные клетки, для которых 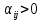и среди данных чисел выбирают максимальное. Клетку с данным числом следует заполнить.

Надо учитывать, что при заполнении данной клетки необходимо изменить объем поставок в нескольких других клетках.

Определение 4. Циклом в таблице условий транспортной задачи называется ломанная линия, вершины которой расположены в занятых клетках таблицы, а звеня расположены вдоль строк и столбцов. В каждой вершине цикла встречается два звена, одно из которых находится в строке, а другой в столбце.

Если ломаная линия, образующая цикл, самопересекается, то место пересечения не является вершиной. Некоторые циклы представлены на рисунке ниже:



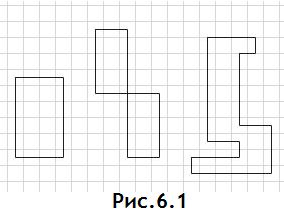
При правильном строении опорного плана для любой свободной клетки можно построить только один цикл. После построения цикла следует перейти к новому опорному плану. Для этого в каждой из клеток, находящихся на вершине цикла записывают определённый знак "+" или "−" . В свободной клетке записывают знак "+" и поочерёдно проходя по циклу записывают знаки "−" и "+". Назовём клетки с записанными в них знаками плюсовыми и минусовыми.

Далее в свободную клетку переносят меньшее из чисел 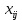, находящихся в минусовых клетках. Это число прибавляют к числам

---

, стоящим в плюсовых клетках, а вычисляют из чисел, стоящих в минусовых клетках. Клетка, которая была свободной, становится занятой, а минусовая клетка с минимальным из чисел , находящихся в минусовых клетках считается свободным.

В результате вышеуказанных перемещений груза по циклу, получим новый опорный план транспортной задачи. Описанный переход от одного опорного плана транспортной задачи к другому опорному плану называется сдвигом по циклу пересчёта.

При сдвиге по циклу пересчёта число занятых клеток не изменяется и равно . Если в минусовых клетках имеется два и более одинаковых минимальных числа , то освобождают только одну, а остальные оставляют занятыми с нулевыми значениями.

Далее полученный опорный план проверяют на оптимальность. Для этого определяют потенциалы пунктов отправления и назначения и находят числа для всех свободных клеток. Если среди них не окажется положительных, то получен оптимальный план. Если же среди них есть положительный, то нужно перейти к новому опорному плану. После конечного числа шагов получают оптимальный план.

Таким образом, алгоритм нахождения оптимального плана содержит следующие этапы:

1. 
   Нахождение опорного плана. При этом число заполненных клеток должно быть равным .
   
2. 
   Нахождение потенциалов и (i=1,..,m; j=1,...,n) пунктов отправления и назначения соответственно.
   
3. 
   Определение числа для каждой свободной клетки. Если среди нет положительных, то получен оптимальный план транспортной задачи. Если же они имеются, то делается переход к новому опорному плану.
   
4. 
   Выбор максимального среди положительных чисел . Определение свободной клетки, которую нужно заполнить. Построение цикла пересчёта для выбранной свободной клетки. Сдвиг по циклу пересчёта.
   
5. 
   Проверка полученного опорного плана на оптимальность, т.е. переход к пункту 2.
   

---

В некотором шаге опорный план может стать вырожденным. Чтобы избежать зацикливания следует преобразовать выраженный план в невыраженный путём замены соответствующих нулевых элементов опорного плана на сколь угодно малыми положительными числами δ и решить задачу. После решения, в оптимальном плане нужно заменить δ нулём.

Рассмотрим метод потенциалов на Примере 4. Решить транспортную задачу, заданную в таблице условий методом потенциалов:

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
A1	2	3	1	2	150
A2	3	4	5	1	100
A3	3	6	3	4	100
Потребности	140	100	70	40	0

Найдём сначала опорный план с помощью одного из методов описанного выше. Пусть это будет метод минимального элемента. Тогда после шагов получим следующую таблицу с опорным планом:

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
A1	2 80	3	1 70	2		0 [ 150 ]
A2	3 60	4	5	1 40		0 [ 100 ]
A3	3	6 100	3	4		0 [ 100 ]
Потребности	0 [ 140 ]	0 [ 100 ]	0 [ 70 ]	0 [ 40 ]		350

---

Опорный план имеет следующий вид:

При этом плане стоимость перевозок вычисляется так:

Проверяем полученный опорный план на оптимальность. Для этого находим потенциалы пунктов отправления и назначения. Для заполненных клеток составляем систему из 6 уравнений с 7 неизвестными:



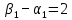
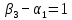
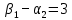
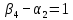
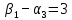
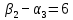
Полагая 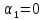 , находим  .

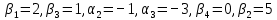Для каждой свободной клетки вычисляем число   

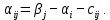
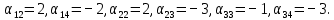
Полученные числа заключаем в рамки и записываем их в соответствующие клетки таблицы:

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
A1	2 80	3 2	1 70	2 －2	150
A2	3 60	4 2	5 －3	1 40	100
A3	3 0	6 100	3 －1	4 －3	100
Потребности	140	100	70	40	350

---