Файл: Реферат по дисциплине Математическое моделирование на тему транспортная задача.docx

2.2 Метод минимального элемента

В отличие от метода северо-западного угла, в методе минимального элемента выбор пунктов отправления и пунктов назначения производится ориентируясь на тарифы перевозок, т.е. в каждом шаге нужно выбрать клетку с минимальным тарифом перевозок. Если таких клеток несколько, то выбираем один из них. Надо отметить, что при данном методе определения заполняемой клетки, стоимость перевозок как правило бывает меньше, чем при методе северо-западного угла. Поэтому целесообразно начальный опорный план найти методом минимального элемента.

Рассмотрим метод минимального элемента на примере.

Пример 2. Найти опорный план транспортной задачи представленной в таблице условий ниже методом минимального элемента:

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
A1	2	3	1	2	150
A2	3	4	5	1	100
A3	3	6	3	4	100
Потребности	140	100	70	40	0

Число пунктов отправления , а число пунктов назначения . Следовательно, опорный план задачи определяется числами, стоящими в заполненных клетках таблицы. Тарифы перевозок единицы груза из каждого пункта отправления во все

---

пункты назначения задаются матрицей



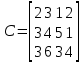
Наличие груза у поставщиков равно: 

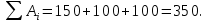
Общая потребность в грузе в пунктах назначения равна: 

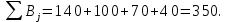
 Модель транспортной задачи является закрытой. Следовательно, она разрешима.

Минимальный тариф равный 1 находится в клетке (A₁, B₃). Поэтому заполняем эту клетку.

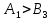. Следовательно, в клетку (A₁, B₃) помещаем число 70. Потребности пункта B₃ полностью удовлетворены. Поэтому исключаем из рассмотрения столбец B₃ и будем считать запасы пункта A₁ равными 150−70=80.

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
A1	2	3	1 70	2		80 [ 150 ]
A2	3	4	5	1		100 [ 100 ]
A3	3	6	3	4		100 [ 100 ]
Потребности	140 [ 140 ]	100 [ 100 ]	0 [ 70 ]	40 [ 40 ]		350

Минимальный тариф равный 1 находится в клетке (

---

A₂, B₄). Поэтому заполняем эту клетку. 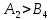. Следовательно, в клетку (A₂, B₄) помещаем число 40. Потребности пункта B₄ полностью удовлетворены. Поэтому, исключаем из рассмотрения столбец B₄ и будем считать запасы пункта A₂ равными .

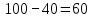Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
A1	2	3	1 70	2		80 [ 150 ]
A2	3	4	5	1 40		60 [ 100 ]
A3	3	6	3	4		100 [ 100 ]
Потребности	140 [ 140 ]	100 [ 100 ]	0 [ 70 ]	0 [ 40 ]		350

Таким образом, продолжая процедуру в -ом шаге получим:

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
A1	2 80	3	1 70	2		0 [ 150 ]
A2	3 60	4	5	1 40		0 [ 100 ]
A3	3	6 100	3	4		0 [ 100 ]
Потребности	0 [ 140 ]	0 [ 100 ]	0 [ 70 ]	0 [ 40 ]		350

---

Запишем полученный опорный план:



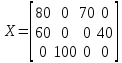
При этом плане стоимость перевозок вычисляется так: .

---

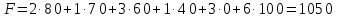2.3 Метод аппроксимации Фогеля

Суть метода аппроксимации Фогеля заключается в следующем. Для каждой строки и для каждого столбца находим разности между двумя записанными в них минимальными тарифами. Полученные разности записываем в специально отведённые для этого столбце и в строке в таблице условий задачи.

Среди указанных разностей выбираем максимальную. В строке (или в столбце), которой данная разность соответствует, определяем минимальный тариф. Клетку, в которой он записан заполняем на данной итерации.

Если минимальный тариф одинаков для нескольких клеток данной строки (столбца), то для заполнения выбираем ту клетку, которая соответствует наибольшей разности между двумя минимальными тарифами в данном столбце (строке).

Применение метода аппроксимации Фогеля позволяет получить либо опорный план, близкий к оптимальному, либо сам оптимальный план.

Рассмотрим метод аппроксимации Фогеля на Примере 2, рассмотренной выше.

Пример 3. Найти опорный план транспортной задачи представленной в таблице условий ниже методом аппроксимации Фогеля:

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
A1	2	3	1	2	150
A2	3	4	5	1	100
A3	3	6	3	4	100
Потребности	140	100	70	40	0

---