Файл: Реферат по дисциплине Математическое моделирование на тему транспортная задача.docx
Добавлен: 07.11.2023
Просмотров: 204
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Среди чисел
 есть положительные. Следовательно, данный опорный план не является оптимальным. Наибольшее положительное число 2 находится в пересечении строки A1 и столбца B2. Для данной свободной клетки строим цикл пересчёта. Для этого вставим в эту клетку знак "+" а остальные клетки цикла поочерёдно знаки "−" и "+".
есть положительные. Следовательно, данный опорный план не является оптимальным. Наибольшее положительное число 2 находится в пересечении строки A1 и столбца B2. Для данной свободной клетки строим цикл пересчёта. Для этого вставим в эту клетку знак "+" а остальные клетки цикла поочерёдно знаки "−" и "+".| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 | 2 - 80 | 3 + 2 | 1 70 | 2 -2 | 150 |
| A2 | 3 60 | 4 2 | 5 -3 | 1 40 | 100 |
| A3 | 3 + 0 | 6 - 100 | 3 -1 | 4 -3 | 100 |
| Потребности | 140 | 100 | 70 | 40 | 350 |
Наименьшее из чисел в минусовых клетках равно 80. Клетка, в которой находится это число становится свободной. В новой таблице другие числа получаются так. Числам, находящимся в плюсовых клетках добавляется 80, а из чисел, находящихся в минусовых клетках вычитается это число.
| Пункты отправления | Пункты назначения | Запасы | ||||
| B1 | B2 | B3 | B4 | |||
| A1 | 2 | 3 80 | 1 70 | 2 | 150 | |
| A2 | 3 60 | 4 | 5 | 1 40 | 100 | |
| A3 | 3 80 | 6 20 | 3 | 4 | 100 | |
| Потребности | 140 | 100 | 70 | 40 | 350 | |
Опорный план имеет следующий вид:
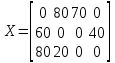 | |
| | |
При этом плане стоимость перевозок вычисляется так:
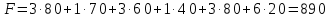
Проверяем полученный опорный план на оптимальность. Для этого находим потенциалы пунктов отправления и назначения. Для заполненных клеток составляем систему из 6 уравнений с 7 неизвестными:
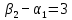      | |
| | |
Полагая
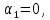 находим
находим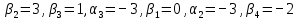 .
.Для каждой свободной клетки вычисляем число
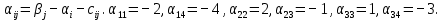
Полученные числа заключаем в рамки и записываем их в соответствующие клетки таблицы:
| Пункты отправления | Пункты назначения | Запасы | ||||
| B1 | B2 | B3 | B4 | |||
| A1 | 2 -2 | 3 80 | 1 70 | 2 -4 | 150 | |
| A2 | 3 60 | 4 2 | 5 -1 | 1 40 | 100 | |
| A3 | 3 80 | 6 20 | 3 1 | 4 -3 | 100 | |
| Потребности | 140 | 100 | 70 | 40 | 350 | |
Среди чисел
 есть положительные. Следовательно, данный опорный план не является оптимальным. Наибольшее положительное число 2 находится в пересечении строки
есть положительные. Следовательно, данный опорный план не является оптимальным. Наибольшее положительное число 2 находится в пересечении строки  и столбца
и столбца 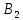 . Для данной свободной клетки строим цикл пересчёта. Для этого вставим в эту клетку знак "+" а остальные клетки цикла поочерёдно знаки "−" и "+".
. Для данной свободной клетки строим цикл пересчёта. Для этого вставим в эту клетку знак "+" а остальные клетки цикла поочерёдно знаки "−" и "+".| Пункты отправления | Пункты назначения | Запасы | ||||
| B1 | B2 | B3 | B4 | |||
| A1 | 2 -2 | 3 80 | 1 70 | 2 -4 | 150 | |
| A2 | 3 - 60 | 4 + 2 | 5 -1 | 1 40 | 100 | |
| A3 | 3 + 80 | 6 - 20 | 3 1 | 4 -3 | 100 | |
| Потребности | 140 | 100 | 70 | 40 | 350 | |
Наименьшее из чисел в минусовых клетках равно 20. Клетка, в которой находится это число становится свободной. В новой таблице другие числа получаются так. Числам, находящимся в плюсовых клетках добавляется 20, а из чисел, находящихся в минусовых клетках вычитается это число.
| Пункты отправления | Пункты назначения | Запасы | |||
| B1 | B2 | B3 | B4 | ||
| A1 | 2 | 3 80 | 1 70 | 2 | 150 |
| A2 | 3 40 | 4 20 | 5 | 1 40 | 100 |
| A3 | 3 100 | 6 | 3 | 4 | 100 |
| Потребности | 140 | 100 | 70 | 40 | 0 |
Опорный план имеет следующий вид:
| |
При этом плане стоимость перевозок вычисляется так:
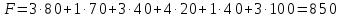
Проверяем полученный опорный план на оптимальность. Для этого находим потенциалы пунктов отправления и назначения. Для заполненных клеток составляем систему из 6 уравнений с 7 неизвестными:
   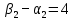  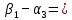 3 3 | |
| | |
Полагая
 находим
находим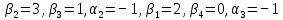 .
.Для каждой свободной клетки вычисляем число
 .
. 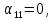
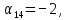
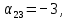
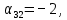
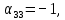
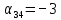
Среди чисел
 нет положительных. Следовательно, данный опорный план является оптимальным. Оптимальный план имеет следующий вид:
нет положительных. Следовательно, данный опорный план является оптимальным. Оптимальный план имеет следующий вид: 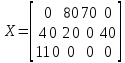 | |
При этом плане стоимость перевозок вычисляется так:
 .
.Заключение
В работе изложены основные подходы и методы решения транспортной задачи. Решение данной задачи позволяет разработать в наибольшей мере рациональные пути и способы транспортирования товаров, устранить чрезмерно дальние, встречные, повторные перевозки. Все это сокращает время продвижения товаров, уменьшает затраты предприятий и фирм, связанные с осуществлением процессов снабжения сырьём, материалами, топливом, оборудованием и т.д.
Алгоритм и методы решения транспортной задачи могут быть использованы при решении некоторых экономических задач, не имеющих ничего общего с транспортировкой груза. В этом случае величины тарифов
 имеют различный смысл в зависимости от конкретной экономической задачи. К таким задачам относятся следующие: оптимальное закрепление за станками операций по обработке деталей. В них
имеют различный смысл в зависимости от конкретной экономической задачи. К таким задачам относятся следующие: оптимальное закрепление за станками операций по обработке деталей. В них  является экономическим показателем производительности. Задача позволяет определить, сколько времени и на какой операции нужно использовать каждый из станков, чтобы обработать максимальное количество деталей. Так как транспортная задача требует нахождения минимума, то значения
является экономическим показателем производительности. Задача позволяет определить, сколько времени и на какой операции нужно использовать каждый из станков, чтобы обработать максимальное количество деталей. Так как транспортная задача требует нахождения минимума, то значения  берутся с отрицательным знаком. Имеется
берутся с отрицательным знаком. Имеется 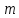 механизмов, которые могут выполнять
механизмов, которые могут выполнять 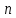 различных работ с производительностью
различных работ с производительностью 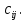 Задача позволяет определить, какой механизм и на какую работу надо назначить, чтобы добиться максимальной производительности. И это лишь один из вариантов применения транспортной задачи. Таким образом, важность решения данной задачи для экономики несомненна.
Задача позволяет определить, какой механизм и на какую работу надо назначить, чтобы добиться максимальной производительности. И это лишь один из вариантов применения транспортной задачи. Таким образом, важность решения данной задачи для экономики несомненна.