Файл: Решение систем линейных уравнений методом подстановки.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Конспект урока по теме:
«Решение систем линейных уравнений методом подстановки»
7 класс
Составила:
Учёнова Наталья Николаевна
учитель математики МОУ СОШ № 22
Тема урока: Решение систем линейных уравнений методом подстановки.
Учебник: Алгебра: 7 класс: учебник для учащихся образовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.
Тип урока: урок изучения нового материала.
Цель урока: формирование у учащихся умения решать системы линейных уравнений с двумя неизвестными способом подстановки.
Задачи:
Образовательные: повторить понятие, что называется решением системы линейный уравнений, что значит, решить систему линейных уравнений с двумя неизвестными, познакомиться с алгоритмом решения системы двух линейных уравнений с двумя неизвестными методом подстановки, обобщить и систематизировать знания и умения обучающихся при решении систем линейных уравнений с двумя переменными.
Развивающие: развивать математический и общий кругозор, мышление и речь обучающихся, способствовать формированию умений применять приёмы: обобщения, сравнения, выделения главного.
Воспитательные: формировать интерес к математике, к познанию нового, умению анализировать, сравнивать, организованности и взаимопомощи через работу в парах.
Планируемые результаты:
Предметные:
Знать, что такое решить систему линейных уравнений с двумя переменными, что называется решением системы уравнений с двумя переменными, умение применять на практике графический метод решения систем двух линейных уравнений и метод подставки;
уметь выражать одну переменную через другую, полученный результат подставлять в другое уравнение, решать уравнение с одной переменной.
Мета предметные:
Познавательные: умение работать с новой информацией, умение анализировать, синтезировать, сравнивать полученный результат;
Регулятивные: осуществлять контроль своих знаний и умений в процессе достижения результата в форме сравнений решений различными способами и его результата с заданным образцом с целью обнаружения ошибок, корректировать свои действия в случае расхождения
Коммуникативные
: обнаружение и формулирование обучающимися учебной проблемы совместно с учителем; высказывание своего предположения, умение определить и сформулировать цель урока с помощью учителя, умение вступать в диалог с учителем и одноклассниками, участвовать в коллективном обсуждении;
Личностные:
формировать желание учиться и приобретать новые знания, не останавливаться перед трудностями и искать пути их решения, умение осуществлять самооценку успешности своей учебной деятельности.
Методы: фронтальный, частично–поисковый, коллективный, индивидуальный.
Оборудование: учебник, проектор, экран, раздаточный материал.
Ход урока
-
Организационный момент
Учащиеся перед началом урока делятся на группы.
Деятельность учителя
Учитель приветствует учащихся, проверяет их готовность к уроку, создает положительный настрой и выбирает ответственного ученика в каждой группе.
Деятельность учащихся
Приветствуют учителя. Проверяют готовность к уроку, настраиваются на получение новых знаний.
-
Проверка домашнего задания
Деятельность учителя
Включает слайд 1, 2. Отвечает на вопросы учащихся, если что-то непонятное встретилось в домашней работе.
Деятельность учащихся
Самопроверка по готовым ответам. Задают вопросы по домашней работе. Обсуждают. Самооценка. Исправление ошибок. Сдают работы на проверку.
Слайд 1.
№ 1. Решить графически систему уравнений:
Построим график первого уравнения линейной функции
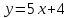
| Х | 0 | -1 |
| У | 4 | 1 |
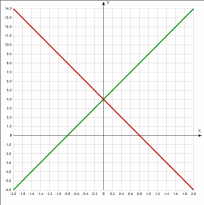Построим график второго уравнения линейной функции
| Х | 0 | 1 |
| У | 4 | -1 |
Мы видим по графику, что точка пересечения графиков имеет координаты (0;4). Эта пара чисел и будет решение этой системы уравнений.
Ответ: (0;4).
Слайд 2.
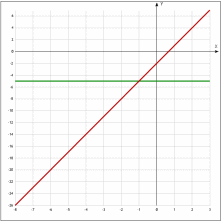№ 2. Решить графически систему уравнений: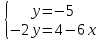
преобразуем 2-ое уравнение, разделив обе части уравнения на -2, получим:
у= - 5 это прямая, параллельная оси абсцисс
Построим график второго уравнения линейной функции
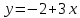
| Х | 0 | -1 |
| У | -2 | -5 |
Мы видим по графику, что точка пересечения графиков имеет координаты (-1;-5). Эта пара чисел и будет решение этой системы уравнений.
Ответ: (-1;-5).
-
Устный счёт
Деятельность учителя
Учитель предлагает учащимся найти пару чисел, которая является решением системы. Выводит на экран слайд 3.
Деятельность учащихся
Учащиеся подставляют поочередно пары чисел в систему уравнений, считают, поднимают руку и называют ответ. Обосновывают решения.
Слайд 3
Какая из пар чисел (-5;1), (1;4), (2;3) является решением системы уравнений
-
Актуализация знаний
Деятельность учителя
Учитель предлагает учащимся вспомнить основные понятия из ранее изученного материала, задаёт вопросы:
Что будет решением уравнения с двумя переменными?
Что значит решить уравнение с двумя переменными?
Свойства уравнений с двумя переменными?
Что будет решением системы?
Что значит решить систему?
Деятельность учащихся
Учащиеся отвечают на вопросы учителя. Повторяют основные понятия, которые им понадобятся для изучения новой темы.
-
Постановка целей, задач урока, мотивация учебной деятельности учащихся
Деятельность учителя
Учитель задает наводящие вопросы:
Мы научились решать системы уравнений графическим способом, строив графики.
Мы знаем свойства уравнений с двумя переменными и умеем их применять.
Как вы думаете, что можно сделать с уравнениями в системе?
Как вы думаете, как можно другим способом решить систему уравнений?
Как называется такой метод?
С каким методом решения системы уравнений мы познакомимся?
Чему мы должны научиться на этом уроке?
Деятельность учащихся
Отвечают на вопросы.
Формулируют цели и задачи урока.
Формулируют тему урока.
-
Изучение нового материала.
Алгоритм решения системы двух уравнений с двумя переменными методом подстановки
Деятельность учителя
Учитель вводит новый способ решения системы двух уравнений с двумя переменными методом подстановки. Объясняет учащимся алгоритм решения методом подстановки. Решает вместе с учащимися у доски задание с помощью алгоритма решения системы уравнений методом подстановки.
Алгоритм:
-
Выразить из любого уравнения системы одну переменную через другую
2. Подставить в другое уравнение системы вместо этой переменной выражение, полученное на первом шаге;
3. Решить уравнение с одной переменной, полученное на втором шаге;
4. Подставить найденное значение переменной в выражение, полученное на первом шаге;
5. Вычислить значение другой переменной;
6. Записать ответ.
Деятельность учащихся
Учащиеся внимательно слушают объяснения учителя, записывают себе схематично алгоритм. Один из учащихся по желанию выходит к доске, остальные в это время работают в тетрадях.
№ 1.
1 шаг. Из уравнения (1) выразим х:
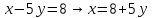
2 и 3 шаг. Подставим х в уравнение (2):
2х+4у=30
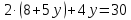
16 + 10у + 4у = 30
14у = 30 – 16
14у = 14
У =14 : 14
У=1
4 и 5 шаг. Найденное значение у=1 подставим в
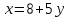
Получим
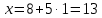. Пара чисел (х;у) будет решением системы, в данном случае (13;1)
Проверка
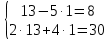
6 шаг. Ответ: (13;1)
-
Первичное закрепление материала
Деятельность учителя
Решает вместе с учащимися у доски несколько заданий с помощью алгоритма решения системы уравнений методом подстановки.
Деятельность учащихся
Учащиеся внимательно слушают объяснения учителя. Один из учащихся по желанию выходит к доске, остальные в это время работают в тетрадях.
| № 2 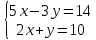   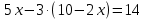 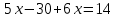   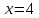 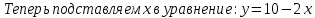 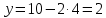 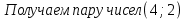 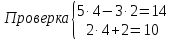 Ответ: (4;2) | № 3 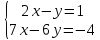 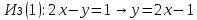 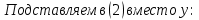    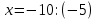  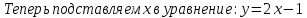 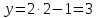 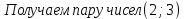  Ответ: (2;3) |
-
Самостоятельная работа
Деятельность учителя
Раздает карточки с заданиями. Объясняет в чем заключается задание. Выдает образец решение и ответы, по которым ответственный группы оценит работы учащихся.