Муниципальное бюджетное образовательное учреждение

средняя общеобразовательная школа №4

городского округа г.Выкса Нижегородской области


Графы в математике

Физико-математическое отделение

Секция математическая
Работу выполнила:

ученица 9 класса

Дегтева Алёна Александровна,

15 лет

г.Выкса

2015год

Оглавление:

• 
  Аннотация……………………………………………………………..…. 3
  
• 
  Введение………………………………………………………………..… 4
  
• 
  Глава1. Обзор литературы…………………………………………….. 5
  
• 
  Глава 2. История теории графов……………………………………... 6
  

2.1 Из истории возникновения графов……………………………….. 6-8

2.2. Пионеры теории графов…………………………………………..…. 9

2.3. Азы теории графов……………………………………………..…10-13

2.4. Виды графов……………………………………………………..…. 13

2.2.1. Геометрические и полные графы………………………..…13-15

2.2.2. Плоские графы…………………………………………….…15-18

2.2.3 Деревья…………………………………………………...........18-20

2.2.4.Эйлеровы графы…………………………………………........20-22

• 
  Глава 3. Результаты и их обсуждения…………………………… 23-24
  
• 
  Заключение…………………………………………………………..…. 25
  
• 
  Список использованной литературы……………………….……… 26
  
• 
  Приложения …………………………………………………..……….. 27
  

Аннотация

В данной работе содержатся сведения о современном разделе современной математики – теории графов, которая зародилась в XVIII веке, а большее развитие получила в XX веке; о самих графах, истории их возникновения, их разнообразии. Готовя данную исследовательскую работу, я изучила ряд источников, из которых ясно, что графы – очень интересное понятие, графы помогают сделать решение задач более простым и наглядным.

Цель моей работы: выяснить, что такое граф, и как применить его при решении математических задач.

Мною поставлены следующие задачи:

- познакомиться с историей возникновения теории графов;

- научиться решать задачи с помощью графов;

- подобрать графы, согласно их классификации;

---

- придумать интересные задания для одноклассников.

Основные методы исследования:

Анализ информации следующих источников:

- научной, методической литературы;

- посещение библиотеки, просмотр Интернет-сайтов;

- проведение анкетирования.

На основе этих методов и поставленных мною целей, я получила следующие результаты своей работы:

- собран материал о графах;

- мною подобраны различные графы, согласно их видам;

-создано наглядное пособие «Решаем задачи с помощью графов», презентация.
Введение

Хорошо да коротко – вдвойне хорошо.

Народная мудрость

Я выбрала эту тему для своей исследовательской работы, потому что она меня заинтересовала. Мне было интересно узнать, какие задачи можно решить с помощью графов. В процессе работы я выяснила, что существуют различные виды графов, с помощью графов легко решать логические задачи и головоломки. Эта тема сейчас актуальна, так как встречаются задачи (например, на олимпиадах), которые не решаются алгебраическими методами, а требуют сложных логических рассуждений. Графы помогают сделать их более понятными и наглядными. Часто, казалось бы, нерешаемая задача, имеет очень простое решение.

Я хочу узнать как можно больше о возникновении графов, об их видах.

Проблема: Отсутствие информации у обучающихся о методах решения задач с помощью графов.

Гипотеза: Использование теории графов способствует успешному решению логических задач.

Цель исследования: отыскать рациональные приёмы и методы для решения логических задач.

Задачи:

- изучить понятие графа;

- изучить элементы теории графов для решения задач;

- разобрать решение различных видов задач;

- выявить роль графов в математике.

Над своим исследованием я работала около трёх месяцев. Посещала школьную библиотеку. Искала информацию, используя ресурсы Интернет-сайтов.

Глава 1. Обзор литературы.

В книге «Графы и их применение» О.Оре 1 я узнала, что графы – сети линий, соединяющих заданные точки, широко применяются в разных разделах математики и в приложениях. Я выбрала данную книгу, так как для ее понимания вполне достаточны минимальные предварительные знания, практически не превышающие курса математики средней школы. Здесь рассматриваются основные понятия теории графов, виды графов, примеры задач, решаемых с помощью графов. Также из этой книги я узнала, что теория графов появилась благодаря одной занимательной задаче о Кёнигсбергских мостах, которую решил Леонард Эйлер. Именно он считается отцом теории графов.

---

В книге «Теория графов» Ф.Харари 2 я рассмотрела эйлеровы графы, узнала, какие графы можно считать эйлеровыми, как решаются задачи на эйлеровы графы.

Из книги «Карты метро и нейронные сети. Теория графов» Клауди Альсина 3 я узнала о том, что еще до создания теории графов многие ученые совершенно независимо друг от друга использовали понятия, которые впоследствии были объединены в теорию графов. Развитию теории графов в немалой степени способствовали такие выдающиеся ученые , как Уильям Томас Татт, Фрэнк Харари, Эдсгер Вибе Дейкстра и Пол Эрдёш. Теория графов приобрела большую известность благодаря их исследованиям, нестандартным задачам и написанными справочниками.

В журнале «Математика для школьников» 4 рассматриваются различные логические задачи, решаемые методом графов. Некоторые из них я использовала для создания наглядного пособия «Решаем задачи с помощью графов».

Также задачи для самостоятельного решения я взяла из книги М.И.Зайкина «Математический тренинг» 5.


Глава 2. История теории графов.

Теория графов - (англ. theory, graph; нем. Graphentheorie) в узком смысле - раздел дискретной математики, одна из ветвей дискретной топологии, в широком смысле - теория сетей, наука о топологических формах, сетевых моделях представления любого процесса или системы. Основным объектом исследования этой теории являются графы.

Граф — основной объект изучения математической теории графов, совокупность непустого множества вершин и наборов пар вершин (связей между вершинами).

Граф задается множеством точек или вершин х₁, х₂, ..., х_n и множеством линий или ребер a₁, a₂, ... , a_m, соединяющих между собой все или часть точек. Формальное определение графа может быть дано следующим образом.

Графом называется двойка вида G = (X, A), где X = {x_i}, i = 1, 2, ..., n – множество вершин графа, A = {a_i}, i = 1, 2,... , m – множество ребер графа.

Теория графов содержит большое количество нерешённых проблем и пока не доказанных гипотез.

2.1. Из истории возникновения графов

Теория графов появилась благодаря одной занимательной задаче, которую решил Леонард Эйлер. История гласит, что в 1736 году блестящий математик остановился в Кёнигсберге (в настоящее время - Калининград). Город был разделен рекой на четыре части, которые были соединены семью мостами.

---

На рисунке представлен упрощенный план города, на котором мосты обозначены цифрами.



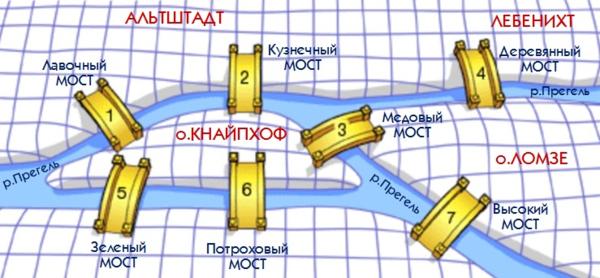
Эйлер писал об этой задаче: «Насколько я понимаю, это задача широко известна. Она формулируется так: в прусском городе Кёнигсберге есть остров под названием Кнайпхоф, окруженный двумя рукавами реки Преголя. Через два рукава реки перекинуто семь мостов. Нужно определить, можно ли обойти все мосты, пройдя по каждому ровно один раз. Мне сообщили, что некоторые утверждают, будто это невозможно, другие сомневаются, но никто не верит, что это и в самом деле возможно».

Сам Эйлер определил, что решить задачу невозможно, приведя следующие рассуждения. Расположение районов города можно представить на схеме, где четырём точкам A, B, C и D соответствуют четыре района города, а кривым, соединяющим эти точки, - мосты:



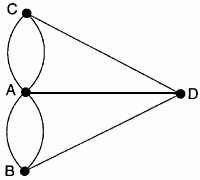
Таким образом, исходная задача эквивалентна следующей, проиллюстрированной рисунком выше: можно ли провести маршрут так, что каждая кривая будет пройдена ровно один раз? Если бы это было возможно, то число линий для каждой точки должно было быть четным. Однако число линий для каждой точки на схеме является нечетным. Следовательно, задача не имеет решения.

Кёнигсбергские мосты были разрушены во время Второй мировой войны, но эта история, авторство которой приписывается Эйлеру, дала начало удивительно полезной и красивой математической теории – теории графов. Нужно учитывать, что ещё до её создания многие ученые совершенно независимо друг от друга использовали понятия, которые впоследствии были объединены в теорию графов.

В 1847 году Густав Кирхгоф использовал схемы, подобные графам, при изучении электрических цепей. В 1857 году Артур Кэли изучал число изомеров органического соединения с помощью графов, в которых точки соединялись между собой одной или четырьмя линиями – по числу химических связей. В 1869 году Мари Энмон Камиль Жордан занимался анализом абстрактных древовидных структур. В 1859 году ирландский математик Уильям Роуэн Гамильтон придумал игру, цель которой – обойти вершины многогранника. Несколько лет спустя на основе этой игры были созданы гамильтоновы цепи

---

, которые имеют очень интересное применение.

В 1852 году возникла задача о раскраске карт таким образом, чтобы страны с общей границей были окрашены в разные цвета. Эта задача дала начало множеству исследований графов. Психолог Курт Левин ввёл в психологию схемы, на которых люди обозначались точками, а личные отношения между ними – линиями. Физики Уленбек, Ли и Янг использовали схемы из точек и линий для изображения структур молекул и взаимодействия между ними.

Во всех случаях конкретная задача изображалась в виде графической схемы, или графа, состоящего из точек и соединяющих их линий. Соответственно, в ходе решения задачи использовался анализ графа. Так как одинаковые графические схемы могут описывать совершенно различные задачи, изучение этих схем позволит найти решение для множества задач одновременно. Разумеется, при построении графа всегда остаются неучтенными какие-то условия и параметры, так как граф должен быть простым. Заметим также, что построение графа не относится к задачам метрической геометрии, то есть точки графа могут соединяться линиями произвольной формы. Главное – отобразить отношения, связи и взаимодействия, а не построить фотографически точную сеть линий и точек.

Графы связаны с комбинаторикой, дискретной математикой, топологией, теорией алгоритмов, теорией узлов и другими разделами математики. Многие математические теории способствовали развитию теории графов, а те в свою очередь позволили решить множество задач в других дисциплинах.

2.2. Пионеры теории графов

Развитию теории графов в немалой степени способствовали такие выдающиеся ученые, как Уильям Томас Татт, Фрэнк Харари, Эдсгер Вибе Дейкстра и Пол Эрдёш. Теория графов приобрела большую известность благодаря их исследованиям, нестандартным задачам и написанным ими справочникам.

Британский ученый Уильям Томас Татт (1917-2002) изучал химию, но интерес к занимательным математическим задачам заставил его сменить сферу деятельности. В итоге в 1948 году он получил степень доктора математики и начал заниматься преподаванием и научной деятельностью.

Его 168 статей и несколько блестящих книг особенно обогатили теорию графов, а вместе с ней – комбинаторику и дискретную математику. Многие понятия теории графов теперь носят его имя.

---

Смотрите также файлы

• Данный вариант состоит из 6 заданий, включающие вопросы с множественным выбором ответов, требующие краткого и развернутого ответов.docx

• Шыыс азастан облысы білім басармасы скемен аласы бойынша білім беру бліміні 6 орта мектебі кмм 5 А сыныбында ткізілетін Отбасы баыт мекені.doc

• Опишите что такое биг дата Для чего можно использовать На какие характеристики разделяют Big Data.docx

• 11сынып аза тілі бжб аза тілі пнінен 4тосан бойынша жиынты баалау тапсырмалары.doc

• Программа среднего профессионального образования 46. 02. 01 Документационное обеспечение управления и архивоведение Дисциплина математика Практическое задание 2.doc